前言
使用情形
- 情形一:二阶导全为正(或负),就能判断一阶导的增(或减),且一阶导的零点刚好在给定区间的端点处,这样一阶导就是全为正(或全为负)的,原函数就是单调函数;
证明 : 由已知 (f(x)=cfrac{2ln x}{x}+x-5),限定定义域为([1,+infty)) ,
(f'(x)=cfrac{2-2ln x}{x^{2}}+1=cfrac{x^{2}+2-2ln x}{x^{2}}),
设 (h(x)=x^{2}+2-2ln x)此时为何要取分子求其导数,原因是分母的正负我们已经能确定了;另外,从数的角度解不等式不好解,从形的角度不好做图像判断正负,所以利用二阶导判断其正负;,
(h'(x)=2x-cfrac{2}{x}=cfrac{2left(x^{2}-1 ight)}{x}),
当 (x geqslant 1) 时, (h'(x)geqslant 0), (h(x)) 在 ([1,+infty)) 上单调递增,
(h(x)geqslant h(1)=3>0)
所以 (xgeqslant 1) 时, (f'(x)>0), (f(x)) 单调递增 .
〔解释说明〕:本题目中,二阶导(h'(x))(geqslant)(0),则可知一阶导(h(x))[即(f'(x))]单调递增,而一阶导的端点值(h(1))(=)(3)(>)(0)[即(f'(1))(>)(0)],则说明在(x)(geqslant)(1)时,(f'(x))(>)(0),故原函数(f(x))单调递增,得证。
- 情形二:二阶导全为正(或负),能判断一阶导的增(或减),但此时一阶导的零点在给定区间内部,不在端点处,则一阶导有正有负,原函数就不是单调函数;
(1). 求 (f(x)) 的单调性;
解: (f'(x)=1-cfrac{a+1}{x^{2}}-cfrac{a}{x}=cfrac{x^{2}-ax-(a+1)}{x^{2}})
(=cfrac{(x+1)[x-(a+1)]}{x^{2}}),((x>0)),
① 当(a+1leqslant 0)时,即 (a leqslant-1) 时, (f'(x)geqslant 0) 恒成立,( herefore f(x)) 在 ((0,+infty)) 上单调递增;
② 当(a+1>0)时,即(a>-1) 时, 令 (f'(x)<0), 则 (0<x<a+1), 令 (f'(x)>0), 则 (x>a+1),
所以,(f(x)) 在 ((0, a+1)) 上单调递减, 在 ((a+1,+infty)) 上单调递增;
综上: 当 (aleqslant-1) 时, (f(x)) 在 ((0,+infty)) 上单调递增;
当 (a>-1) 时, (f(x)) 在 ((0, a+1)) 上单调递减, 在 ((a+1,+infty)) 上单调递增 .
(2). 若 (a>0), 且 (f(x)) 的最小值小于 (4-2ln 3), 求 (a) 的取值范围 .
解: 由 (1) 知 (f(x)_{min}=f(a+1)=a+1+1-aln(a+1)),
则(a+2-aln(a+1)<4-2ln2), 即 (a-aln (a+1)<2-2ln 3),
令 (g(x)=x-xln(x+1)),(x>-1),
则(g'(x)=1-ln(x+1)-cfrac{x}{x+1}=-ln(x+1)+cfrac{1}{x+1}),
令 (h(x)=-ln(x+1)+cfrac{1}{x+1}), (h'(x)=-cfrac{1}{x+1}-cfrac{1}{(x+1)^{2}}<0),
所以 (h(x)) 在 ((-1,+infty)) 上单调递减, 又 (h(0)=1>0), (h(1)=cfrac{1}{2}-ln2<0)此处使用函数的零点存在性定理,目的为确定函数在区间((0,1))内的零点。 ,
,
所以存在 (x_{0}in(0,1)), 使得 (hleft(x_{0} ight)=0),
即 (g'left(x_{0}
ight)=0), (g(x))在 (left(0, x_{0}
ight)) 上单调递增, 在 (left(x_{0},+infty
ight)) 上单调递减利用单调性做出函数的大致示意图,如图所示,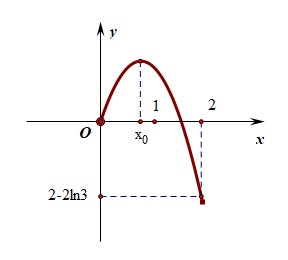 ,
,
又 (g(0)=0>2-2ln 3), (g(2)=2-2ln 3),
所以,(g(a)<2-2ln3) (Leftrightarrow) (a>2)
所以,(a) 的取值范围为 ((2,+infty)) .