复合函数的单调区间求解

前言

研究复合函数的单调性，应该首先求解其定义域。

典例分析

已知函数(f(x)=log_2(x^2-3x+2))，求其单调性。

分析：令(u=x^2-3x+2)，则原复合函数拆分为外函数(y=f(u)=log_2u)和内函数(u=x^2-3x+2)

由(u=x^2-3x+2>0)，解得(xin (-infty，1)cup(2，+infty))，

即此复合函数的定义域为(xin (-infty，1)cup(2，+infty))。

那么要研究其单调性，必须先在上述定义域范围内，定义域优先原则。

然后由(u=x^2-3x+2=(x-cfrac{3}{2})^2-cfrac{1}{4})，

则内函数(u(x))在区间((-infty，1))上单调递减，在区间((2，+infty))上单调递增，

而外函数(y=f(u)=log_2u)只是单调递增的，

故复合函数(f(x))在区间((-infty，1))上单调递减，在区间((2，+infty))上单调递增。

【同类题目】已知函数(f(x)=sqrt{x^2-3x+2})，求其单调性。

提示：仿上例完成，复合函数的定义域为(xin (-infty，1]cup[2，+infty))。

复合函数(f(x))在区间((-infty，1])上单调递减，在区间([2，+infty))上单调递增。

已知 (f(x)=8+2x-x^2)，若 (g(x)=f(2-x^2))，则 (g(x))【(qquad)】

$A$.在区间$(-1,0)$内是减函数

$B$.在区间$(0,1)$内是减函数

$C$.在区间$(-2,0)$内是增函数

$D$.在区间$(0,2)$内是增函数

法1：利用复合函数的复合法则求解，复合函数的定义域为 ((-infty,+infty))，

由于外函数(f(x)=8+2x-x^2=-(x-1)^2+9)，对称轴为 (x=1)，在区间 ((-infty,1))上单调递增，在区间 ((1,+infty)) 上单调递减；内函数为 (t=2-x^2)，对称轴为 (x=0)，在区间 ((-infty,0))上单调递增，在区间 ((0,+infty)) 上单调递减；

由于外函数的对称轴为 (x=1)，故令(2-x^2=1)，解得 (x=-1) 和 (x=1)，这样整个定义域就分成了四个部分，

((-infty,-1))和((-1,0))和((0,1))和((1,+infty))，

根据复合函数的单调性，在以上的四个区间上分别讨论如下：

当 (xin(-infty,-1))时，此时内函数(t=2-x^2)单调递增，且(tin(-infty,1))，此时外函数(f(t)=8+2t-t^2)单调递增，故复合函数 (g(x))单调递增；

当 (xin(-1,0))时，此时内函数(t=2-x^2)单调递增，且(tin(1,2))，此时外函数(f(t)=8+2t-t^2)单调递减，故复合函数 (g(x))单调递减；

当 (xin(0,1))时，此时内函数(t=2-x^2)单调递减，且(tin(1,2))，此时外函数(f(t)=8+2t-t^2)单调递减，故复合函数 (g(x))单调递增；

当 (xin(1,+infty))时，此时内函数(t=2-x^2)单调递减，且(tin(-infty,1))，此时外函数(f(t)=8+2t-t^2)单调递增，故复合函数 (g(x))单调递减；

综上所述，故选 (A) .

法2：导数法求单调区间，由题目可知，

(g(x)=f(2-x^2)=8+2(2-x^2)-(2-x^2)^2)，即 (g(x)=-x^4+2x^2+8)，

则 (g'(x)=-4x^3+4x=-4x(x^2-1)=-4x(x+1)(x-1))，借助穿根法做出函数的简图，

从而可知，当(xin (-1,0))时，(f'(x)<0)，故在区间 ((-1,0))上，函数 (g(x))单调递减，故选 (A).

高阶题目

涉及图像的复合函数问题

已知函数(y=f(x))和(y=g(x))在([-2，2])上的图像如图所示，给出下列四个命题：

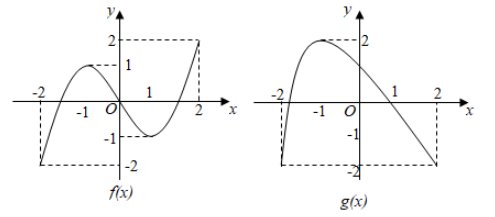
①方程(f[g(x)]=0)有且仅有(6)个根；②方程(g[f(x)]=0)有且仅有(3)个根；

③方程(f[f(x)]=0)有且仅有(5)个根；④方程(g[g(x)]=0)有且仅有(4)个根；

则正确的命题有 _______________。①③④

【法1】：从里向外分析，

对于命题①而言，复合函数为(f[g(x)])；为什么如下选择区间？当我们先选择函数(g(x))的区间为([-2，-1])时，此时虽然能保证内函数(g(x))单调递增，但是此时内函数的值域(g(x)in [-2，2])，其投射到外函数(f(x))上时，就放置到了外函数(f(x))的定义域([-2，2])内，此时外函数的单调性不唯一，说明我们一开始选取的内函数的研究区间([-2，-1])有些大了，所以需要压缩；一直压缩到([-2，x_0])，其中(g(x_0)=-1)，这时候内函数的值域(g(x)in [-2，-1])，刚好投射到外函数的单调递增区间上，说明此时的区间选取是恰当合理的，其他的区间选取与此同理同法；

在([-2，x_0])上，(f[g(x)] earrow)，(f[g(-2)]=f(-2)=-2)，(f[g(x_0)]=f(-1)=1)，其中(g(x_0)=-1);

在([x_0，x_1])上，(f[g(x)]searrow)，(f[g(x_1)]=f(0)=0)，其中(g(x_1)=0)；

在([x_1，x_2])上，(f[g(x)]searrow)，(f[g(x_2)]=f(1)=-1)，其中(g(x_2)=1)；

在([x_2，-1])上，(f[g(x)] earrow)，(f[g(-1)]=f(2)=2)；

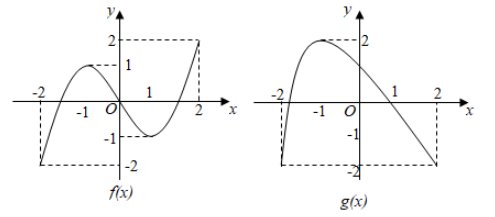
在([-1，0])上，(f[g(x)]searrow)，(f[g(0)]=f(1)=-1)；图中未说明，假定(g(0)=1);

在([0，1])上，(f[g(x)] earrow)，(f[g(1)]=f(-0.3)=0.4)；(g(1)=-0.3)，(f(-0.3)=0.4)为估算值；

在([1，x_3])上，(f[g(x)] earrow)，(f[g(x_3)]=f(-1)=1)，其中(g(x_3)=-1)；

在([x_3，2])上，(f[g(x)]searrow)，(f[g(2)]=f(-2)=-2)；

根据上述函数值，做出函数图像，由图像可知方程(f[g(x)]=0)有且仅有(6)个根；故①正确；

对于命题②而言，复合函数为(g[f(x)])；

在([-2，x_4])上，(g[f(x)] earrow)，(g[f(-2)]=g(-2)=-2)，(g[f(x_4)]=g(-1)=2)，其中(f(x_4)=-1);

在([x_4，x_5])上，(g[f(x)]searrow)，(g[f(x_5)]=g(0)=1)，其中(f(x_5)=0)；

在([x_5，-1])上，(g[f(x)]searrow)，(g[f(-1)]=g(1)=-0.3)；

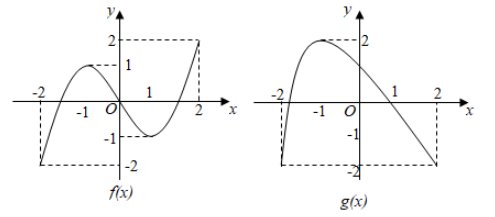
在([-1，0])上，(g[f(x)] earrow)，(g[f(0)]=g(0)=1)；

在([0，1])上，(g[f(x)] earrow)，(g[f(1)]=g(-1)=2)；

在([1，x_6])上，(g[f(x)]searrow)，(g[f(x_6)]=g(1)=0)，其中(f(x_6)=1)；

在([x_6，2])上，(f[g(x)]searrow)，(g[f(2)]=g(2)=-2)；

根据上述函数值，做出函数图像，由图像可知方程(g[f(x)]=0)有且仅有(4)个根；故②错误；

对于命题③而言，复合函数为(f[f(x)])；

在([-2，x_4])上，(f[f(x)] earrow)，(f[f(-2)]=f(-2)=-2)，(f[f(x_4)]=f(-1)=1)，其中(f(x_4)=-1);

在([x_4，x_5])上，(f[f(x)]searrow)，(f[f(x_5)]=f(0)=0)，其中(f(x_5)=0)；

在([x_5，-1])上，(f[f(x)]searrow)，(f[f(-1)]=f(1)=-1)；

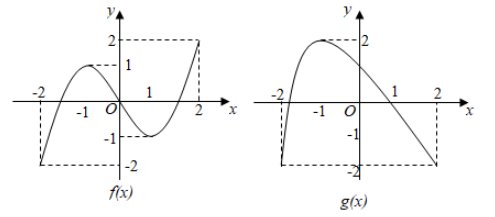
在([-1，0])上，(f[f(x)] earrow)，(f[f(0)]=f(0)=0)；

在([0，1])上，(f[f(x)] earrow)，(f[f(1)]=f(-1)=1)；

在([1，x_6])上，(f[f(x)]searrow)，(f[f(x_6)]=f(1)=-1)，其中(f(x_6)=1)；

在([x_6，2])上，(f[f(x)] earrow)，(f[f(2)]=f(2)=2)；

根据上述函数值，做出函数图像，由图像可知方程(f[f(x)]=0)有且仅有(5)个根；故③正确；

对于命题④而言，复合函数为(g[g(x)])；

在([-2，x_0])上，(g[g(x)] earrow)，(g[g(-2)]=g(-2)=-2)，(g[g(x_0)]=g(-1)=2)，其中(g(x_0)=-1);

在([x_0，x_1])上，(g[g(x)]searrow)，(g[g(x_1)]=f(0)=0)，其中(g(x_1)=0)；

在([x_1，x_2])上，(g[g(x)]searrow)，(g[g(x_2)]=g(1)=-0.3)，其中(g(x_2)=1)；

在([x_2，-1])上，(g[g(x)]searrow)，(g[g(-1)]=g(2)=-2)；

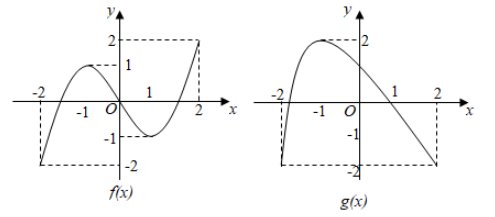
在([-1，0])上，(g[g(x)] earrow)，(g[g(0)]=g(1)=0)；

在([0，1])上，(g[g(x)] earrow)，(g[g(1)]=g(0)=1)；

在([1，x_3])上，(g[g(x)] earrow)，(g[g(x_3)]=g(-1)=2)，其中(g(x_3)=-1)；

在([x_3，2])上，(g[g(x)]searrow)，(g[g(2)]=f(-2)=-2)；

根据上述函数值，做出函数图像，由图像可知方程(g[g(x)]=0)有且仅有(4)个根；故④正确；

综上所述，正确的命题有①③④。

法2：从外向里分析，由图像可知，(-2leqslant g(x)leqslant 2)，(-2leqslant f(x)leqslant 2)，

对于命题①而言，由于满足方程(f[g(x)]=0)的(g(x))有(3)个不同值，由于每个值(g(x))又对应了(2)个(x)值，故满足(f[g(x)]=0)的(x)值有(6)个，即方程(f[g(x)]=0)有且仅有(6)个根，故命题①正确；

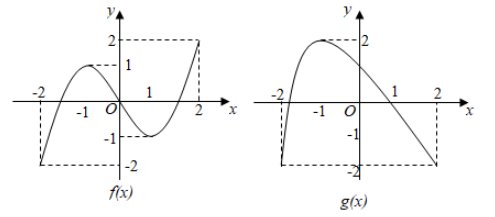
[图像使用方法说明]：由(y=f(x))的图像可以看出，使得(f(x)=0)的三个零点值分别为(x_1=-1.6)，(x_2=0)，(x_3=1.6)[估算]，

在函数(y=g(x))的图像中，分别做直线(g(x)=-1.6)，(g(x)=0)，(g(x)=1.6)，每一条直线和函数(y=g(x))都有(2)个交点，故共有(6)个交点。

对于命题②而言，由于满足方程(g[f(x)]=0)的(f(x))有(2)个不同值，从图中可知，每一个值(f(x))，一个(f(x))的值在((-2，-1))上，另一个(f(x))的值在((0，1))上，当(f(x))的值在((-2，-1))上时，原方程有一个解；当(f(x))的值在((0，1))上时，原方程有(3)个解，故满足(g[f(x)]=0)的(x)值有(4)个，即方程(g[f(x)]=0)有且仅有(4)个根，故命题②不正确；

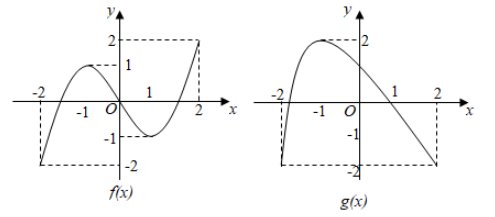
对于命题③而言，由于满足方程(f[f(x)]=0)的(f(x))有(3)个不同值，从图中可知，一个(f(x))的值在((-2，-1))上，一个(f(x))的值为(0)，另一个(f(x))的值在((1，2))上；当(f(x)=0)对应了(3)个不同的(x)值，当(f(x))在((-2，-1))上时，只对应一个(x)值；当(f(x))的值在((1，2))上时，也只对应一个(x)的值，故满足(f[f(x)]=0)的(x)值有(5)个，即方程(f[f(x)]=0)有且仅有(5)个根，故命题③正确；

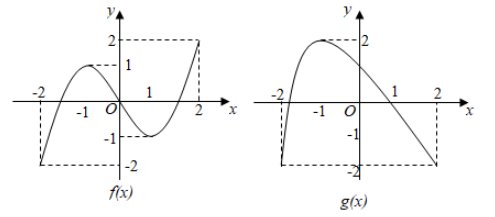
对于命题④而言，由于满足方程(g[g(x)]=0)的(g(x))有(2)个不同值，从图中可知，每个(g(x))的值对应(2)个不同的(x)值，故满足(g[g(x)]=0)的(x)值有(4)个，即方程(g[g(x)]=0)有且仅有(4)个根，故命题④正确；

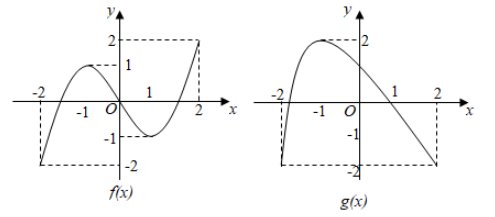
综上所述，正确的命题有①③④。