前言
向量运算中的系数拆分技巧;
相同的话题,还可能出现在数列的运算中;
(nge 2)时,(4S_{n+2}+5S_n=8S_{n+1}+S_{n-1}),
即就是((4S_{n+2}-4S_{n+1})=(4S_{n+1}-4S_n)-(S_n-S_{n-1})),
得到(4a_{n+2}=4a_{n+1}-a_n),变形得到,
(a_{n+2}=a_{n+1}-cfrac{1}{4}a_n),
典例剖析
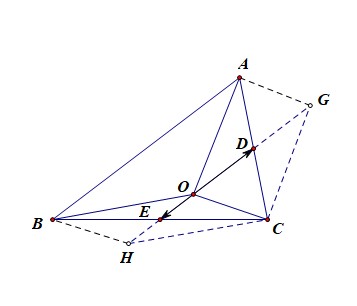
分析:由题目可知(overrightarrow{OA}+2overrightarrow{OB}+3overrightarrow{OC}=vec{0}),
将其系数做恰当的拆分得到,((overrightarrow{OA}+overrightarrow{OC})+2(overrightarrow{OB}+overrightarrow{OC})=vec{0}),
如图即(2overrightarrow{OD}=-4overrightarrow{OE}),即(overrightarrow{OD}=-2overrightarrow{OE}),
即可知点(O)一定在(Delta ABC)的中位线(DE)上,且在中位线上靠近点(E)的三等分点处。
理由如下:以(OA)和(OC)为邻边做平行四边形(AOCG),则点(D)为(AC)的中点,
同理,点(E)为(BC)的中点,则可知(DE)为中位线,又(overrightarrow{OD}=-2overrightarrow{OE}),
则(O、D、E)三点共线,故点(O)一定在(Delta ABC)的中位线(DE)上,且在中位线上靠近点(E)的三等分点处。
令点(B)到边(AC)的高线为(h),则过点(E)和边(AC)平行的直线必然会平分高线(h),
又由于点(O)是(DE)的三等分点之一,故( riangle AOC) 的高为(cfrac{h}{2})的(cfrac{2}{3}),
则(S_{Delta ABC}=cfrac{1}{2}cdot ACcdot h),(S_{Delta AOC}=cfrac{1}{2}cdot ACcdot cfrac{h}{2}cdot cfrac{2}{3}=cfrac{1}{3}cdotcfrac{1}{2}cdot ACcdot h),
故(Delta ABC)的面积与(Delta AOC)的面积之比为3。
【反思总结】:线段等分点的向量给出方式,
二等分点(中点):(overrightarrow{OA}=-overrightarrow{OB}),或(overrightarrow{OA}+overrightarrow{OB}=overrightarrow{0}),则点(O)是(AB)的中点;
三等分点:(overrightarrow{OA}=-2overrightarrow{OB}),或(overrightarrow{OA}+2overrightarrow{OB}=overrightarrow{0}),则点(O)是(AB)的靠近(B)的三等分点;
四等分点:(overrightarrow{OA}=-3overrightarrow{OB}),或(overrightarrow{OA}+3overrightarrow{OB}=overrightarrow{0}),则点(O)是(AB)的靠近(B)的四等分点;

分析:由题目可知(overrightarrow{OA}+2overrightarrow{OB}+3overrightarrow{OC}=vec{0}),
将其系数做恰当的拆分得到,((overrightarrow{OA}+overrightarrow{OC})+2(overrightarrow{OB}+overrightarrow{OC})=vec{0}),
如图即(2overrightarrow{OF}=-4overrightarrow{OE}),即(overrightarrow{OF}=-2overrightarrow{OE}),
即可知(E、O、F)三点共线,且点(O)一定在(Delta ABC)的中位线(EF)上,且在中位线上靠近点(E)的三等分点处。
理由如下:以(OA)和(OC)为邻边做平行四边形(AOCG),则点(F)为(AC)的中点,
同理,点(E)为(BC)的中点,则可知(EF)为中位线,又(overrightarrow{OF}=-2overrightarrow{OE}),
则(E、O、F)三点共线,故点(O)一定在(Delta ABC)的中位线(EF)上,且在中位线上靠近点(E)的三等分点处。
此时连结(BE),由点(O)是( riangle BCF)的重心可知,延长(BO)交(AC)于点(D),
则点(D)必是边(CF)的中点,即(CD=DF),则(AD=2DF=3CD),
过点(O)作(AC)的垂线段,设其高为(h),
由同高不同底可得,(cfrac{S_{Delta COD}}{S_{Delta AOD}}=cfrac{cfrac{1}{2}cdot CDcdot h}{cfrac{1}{2}cdot ADcdot h}=cfrac{1}{3})
【解后反思】当题目告诉(overrightarrow{OA}=2overrightarrow{BO}+3overrightarrow{CO}),则有结论:
①(E、O、F)三点共线,点(O)一定在(Delta ABC)的中位线(EF)上,且在中位线上靠近点(E)的三等分点处。
②延长(BO)交(AC)与点(D),则点(D)是(CF)的中点。
③三等分点出现,常常和三角形的重心,三角形边的中点等联系起来,
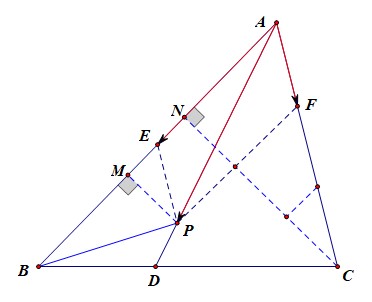
分析:如图,点(E),(F)分别是边(AB),(AC)的二等分点和三等分点,作平行四边形(AEPF),延长(AP)交(BC)于点(D),
则由图可知,( riangle ABP)的高(PM)与( riangle ABC)的高(CN)的关系为(CN=3PM),
故由同底不同高可知,(cfrac{S_{Delta ABP}}{S_{Delta ABC}}=cfrac{cfrac{1}{2}cdot PMcdot AB}{cfrac{1}{2}cdot CNcdot AB}=cfrac{1}{3})
引申:且可知(3BD=2CD)。
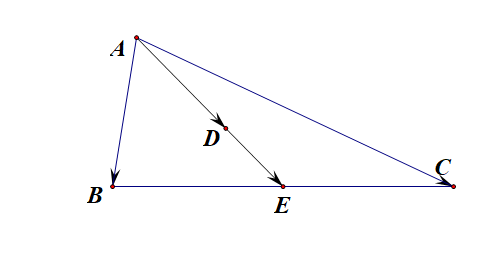
已知(overrightarrow{AB}+overrightarrow{AC}=3overrightarrow{AD}),则(3overrightarrow{AD}=2overrightarrow{AE}),则(overrightarrow{AD}=cfrac{2}{3}overrightarrow{AE}),可知点(D)为( riangle ABC)的重心;
分析:由(4overrightarrow{AD}=overrightarrow{AC}+3overrightarrow{AB}),可得(3overrightarrow{AD}-3overrightarrow{AB}=overrightarrow{AC}-overrightarrow{AD}),
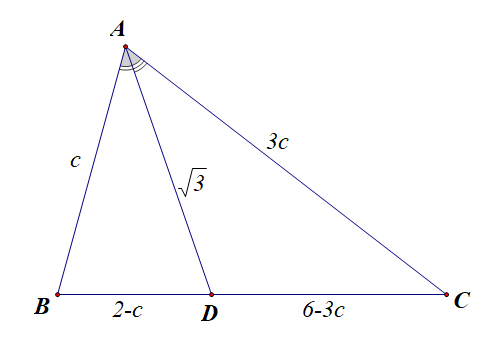
即(3overrightarrow{BD}=overrightarrow{DC}),即(|CD|=3|BD|),又(4c+a=8),
则(a=8-4c=|BC|),(|BD|=cfrac{1}{4}|BC|=2-c),(|CD|=6-2c),
又由于(AD)为(angle BAC)的平分线,由角平分线定理可知,
(cfrac{BD}{CD}=cfrac{AB}{AC}=cfrac{1}{3}),故(|AC|=3c),
在( riangle ABD)与( riangle ACD)中,分别对(angle BAD)和(angle DAC)用余弦定理可得,
(cfrac{3+c^2-(2-c)^2}{2 imes sqrt{3}c}=cfrac{3+(3c)^2-(6-3c)^2}{2 imes sqrt{3} imes 3c})
解得(c=cfrac{5}{4}),(b=cfrac{15}{4}),(a=3)。
解后反思:本题目需要特别注意向量系数的拆分技巧;