割补法

割补法定义

使用场景

• 一般到特殊，

• 四面体割补得到长方体，正四面体割补得到正方体；可以参见下面的数学常识储备。

• 在涉及棱柱和棱锥的外接球中，常考虑使用割补法，具体操作如下：就是把符合条件的棱柱或棱锥放入长方体中，从而把问题转化为长方体的外接球问题，这是转化与划归思想的应用。

适合这种方法的情况小结如下：

①正四面体、三条侧棱两两垂直的正三棱锥、四个面都是直角三角形的三棱锥。

②同一个顶点上三条棱两两垂直的四面体、相对的棱相等的三棱锥。

③若已知棱锥含有线面垂直关系，则可将棱锥补体成长方体或正方体。

④若三棱锥的三个侧面两两垂直，则可将棱锥补体成长方体或正方体。

常识储备

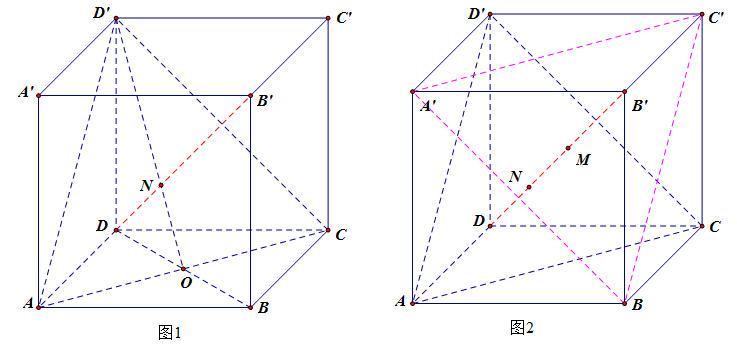
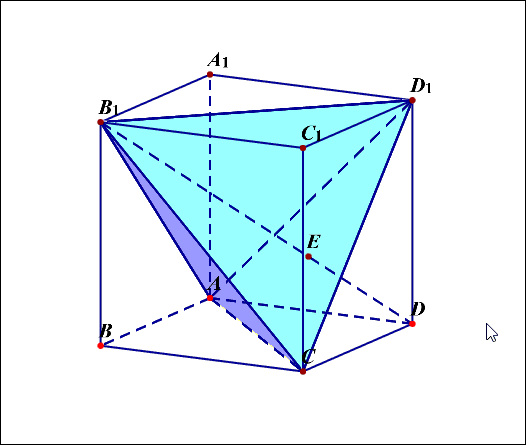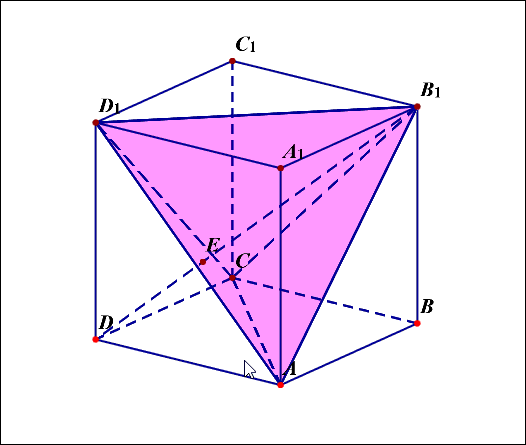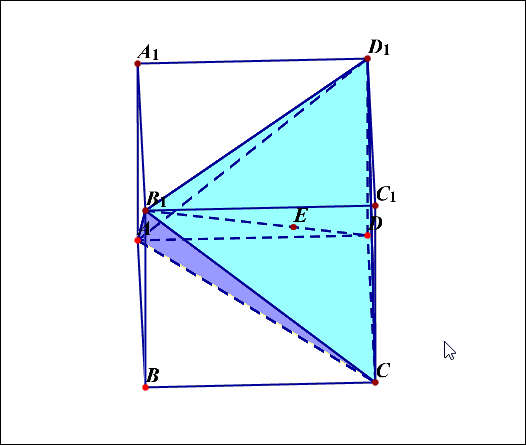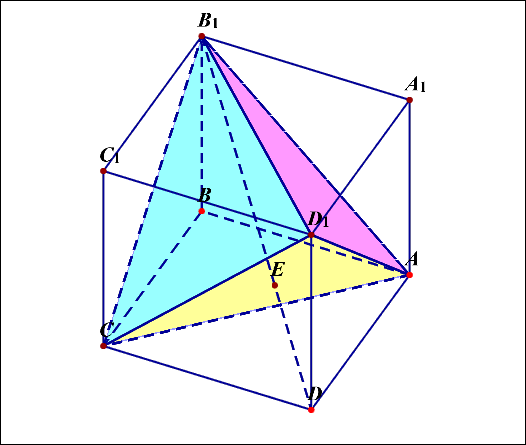
• 如图所示的是正方体(ABCD-A'B'C'D')，有如下的常用结论：

(1)体对角线(B'Dperp)平面(ACD')(如图1)

证明：令体对角线(B'D)和平面(ACD')的交点是(N)，由正四面体(B'-ACD')可知，(N)是三角形底面的中心，连接(OD')，则易知(ACperp BD)，(ACperp BB')，故(ACperp B‘D)，同理(AD'perp B'D)，故体对角线(B'Dperp)平面(ACD')。

(2)(DN=cfrac{1}{3}B'D)(如图1，利用等体积法)

(3)平面(ACD'//A'BC')(如图2)

(4)平面(ACD')与平面(A'BC')的间距是(cfrac{1}{3}B'D)，即体对角线的(cfrac{1}{3})(如图2)

(5)三棱锥(B'-ACD')是正四面体。三棱锥(D-ACD')是正三棱锥。

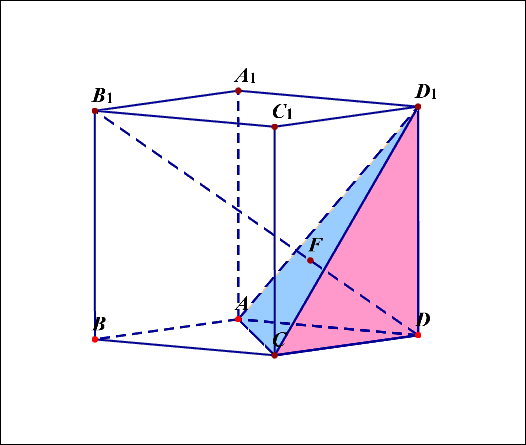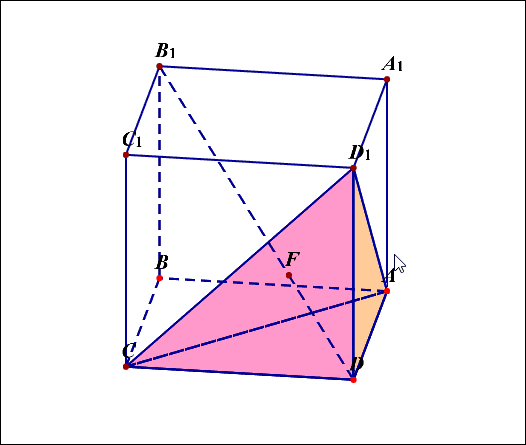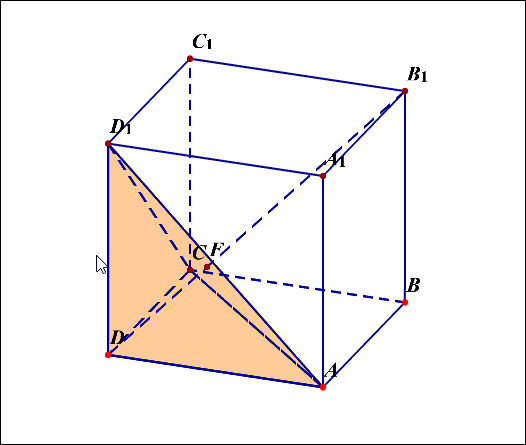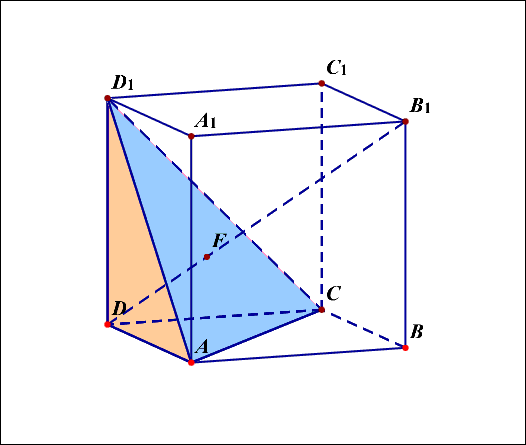
(6)如果需要将正四面体或者墙角型的正三棱锥恢复还原为正方体，我们可以先画出正方体，然后在里面找出需要的正四面体或者墙角型正三棱锥。

典例剖析：

例1【2019届宝鸡市高三理科数学质检Ⅰ第15题】

已知一个四面体(ABCD)的每个顶点都在表面积为(9pi)的球面上，且(AB=CD=a)，(AC=AD=BC=BD=sqrt{5})，则(a)=__________。

分析：如下图所示，构造此四面体，要直接求解(a)，很困难，此时可以考虑将其放置到长方体中，这样我们就想到割补法。

由题意可采用割补法，考虑到四面体(ABCD)的四个面为全等的三角形，所以可在其每个面补上一个以(a)，(sqrt{5})，(sqrt{5})为三边的三角形作为底面，且分别为(x)，(y)，(z)为侧棱长、且侧棱两两垂直的三棱锥，从而可得到一个长、宽、高分别为(x)，(y)，(z)的长方体，

则有(x^2+y^2=5)，(x^2+z^2=5)，(y^2+z^2=a^2)，设球半径为(R)，则有((2R)^2=x^2+y^2+z^2=cfrac{1}{2}a^2+5)，

又由于四面体(ABCD)的外接球的表面积为(9pi)，则球的表面积为(S=4pi R^2=9pi)．

即(4R^2=9)，则(cfrac{1}{2}a^2+5=9)，解得(a=2sqrt{2})。

例2【2017凤翔中学第二次月考理科第15题】

已知三棱锥(P-ABC)满足(PA、PB、PC)两两垂直，且(PA=PB=PC=2)，(Q)是三棱锥(P-ABC)外接球上的一个动点，则点(Q)到平面(ABC)的距离的最大值是多少？

分析：我们可以将此三棱锥还原为正方体的一部分，补体并特殊化为为正方体的一个角，如图所示，

且正方体有个外接球，那么点(Q)到平面(ABC)的距离的最大值即是正方体的体对角线的(cfrac{2}{3})，而体对角线长为(sqrt{2^2+2^2+2^2}=2sqrt{3})，故所求值为(cfrac{4sqrt{3}}{3})。

例3(2017凤翔中学第三次月考理科第10题)

已知球面上有(A、B、C)三点，如果(|AB|=|BC|=|AC|=2sqrt{3})，且球心到平面(ABC)的距离为1，则该球的体积为多少？

分析：本题目关键是求球的半径(R) ，如上例中的模型，已知的三点可以安放在图中的点(A'、B、C')处，但是要注意，

已知的平面(ABC)和模型中的平面(A'BC')平行，不一定重合，此时求半径问题就转化为求正三棱锥的侧棱的长问题了，

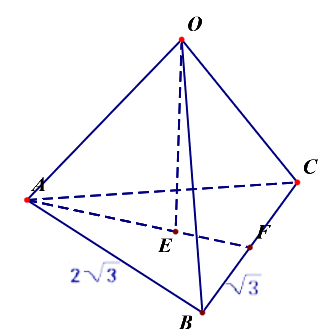
而且此时正三棱锥的底面边长为(2sqrt{3})，正三棱锥的高是1，高的垂足(E)是下底面的中心，

则其侧棱(OA)，(OA=sqrt{1^2+2^2}=sqrt{5})，故(R=sqrt{5})，

故该球的体积(V_球=cfrac{4}{3}cdot picdot R^3=cfrac{20sqrt{5}}{3}pi)。

例4【2019届宝鸡市高三理科数学质检Ⅰ第10题】

已知正三棱柱(ABC-A_1B_1C_1)中，(AB=AA_1=2)，则异面直线(AB_1)与(CA_1)所成角的余弦值为【】

$A.0$ $B.-cfrac{1}{4}$ $C.cfrac{1}{4}$ $D.cfrac{1}{2}$

【法1】空间向量法，第一种建系方式；以点(A)为坐标原点，以(AC)，(AA_1)分别为(y)、(z)轴，以和(AC)垂直的直线为(x)轴，建立如图所示的空间直角坐标系，

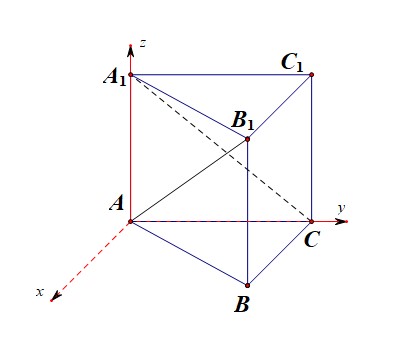
则(A(0，0，0))，(B(sqrt{3}，1，0))，(A_1(0，0，2))，(B_1(sqrt{3}，1，2))，(C(0，2，0))，

(overrightarrow{AB_1}=(sqrt{3}，1，2))，(overrightarrow{A_1C}=(0，2，-2))，且线线角的范围是([0，cfrac{pi}{2}])，

故所求角的余弦值为(|cos<overrightarrow{AB_1}，overrightarrow{A_1C}>|=cfrac{|1 imes 2+2 imes(-2)|}{sqrt{8} imessqrt{8}}=cfrac{1}{4})。故选(C)。

【法2】：立体几何法，补体平移法，将正三棱柱补体为一个底面为菱形的直四棱柱，连结(B_1D)，则(B_1D//A_1C)，

故异面直线(AB_1)与(CA_1)所成角，即转化为共面直线(AB_1)与(B_1D)所成的角(angle AB_1D)，连结(AD)，

在(Delta AB_1D)中，(AB=AA_1=2)，可得(AB_1=B_1D=2sqrt{2})，(AD=2sqrt{3})，

由余弦定理可知，(cosangle AB_1D=cfrac{(2sqrt{2})^2+(2sqrt{2})^2-(2sqrt{3})^2}{2 imes 2sqrt{2} imes 2sqrt{3}}=cfrac{1}{4})，

故所求为(cfrac{1}{4})，故选(C)。

例16【2019届高三理科数学二轮用题】在面积为4的正方形(ABCD)中，(M)是线段(AB)的中点，现将图形沿(MC)，(MD)折起，使线段(MA)和(MB)重合，得到一个四面体(A-CDM)，其中点(B)和点(A)重合，则该四面体外接球的表面积为_________。

分析：平面图形如左图，立体图形如右图所示，(angle MAC=angle MAD=cfrac{pi}{2})，下来的重点是如何将四面体放置在球体内部。

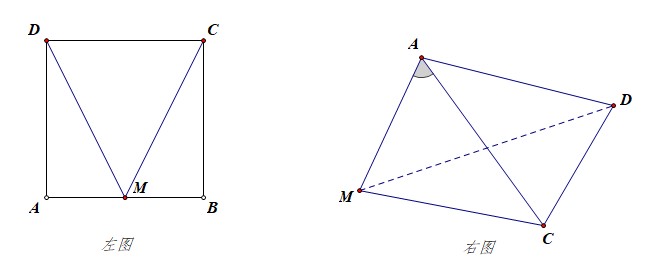
可以这样来思考，将最特殊的面(ACD)放置在下底面，这样方便来放置和下底面垂直的侧棱，如下图所示；

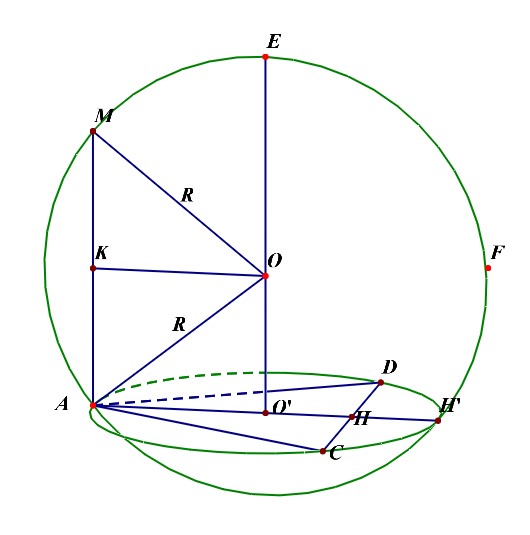
底面圆的圆心(O')为下底面正三角形的重心，(O)为球心，则(OA=OM=R)，由于( riangle ACD)为等边三角形，(AC=2)，则(CH=1)，(AH=sqrt{3})，则(AO'=cfrac{2sqrt{3}}{3})，过点(O)做(OKperp AM)于(K)，则(OK=AO'=cfrac{2sqrt{3}}{3})，又(AK=cfrac{1}{2}AM=cfrac{1}{2})，在(Rt riangle AOK)中，由勾股定理可知(R^2=(cfrac{2sqrt{3}}{3})^2+(cfrac{1}{2})^2=cfrac{19}{12})，故(S_{球O}=4pi R^2=cfrac{19pi}{3})。

补充说明：如果想不清这一点，还可以想着将四面体补体成一个直三棱柱，如下图的动图所示，

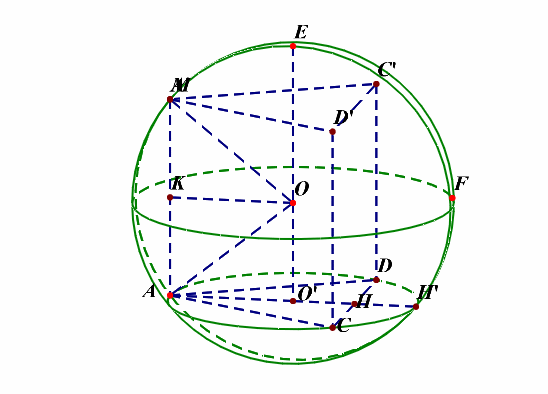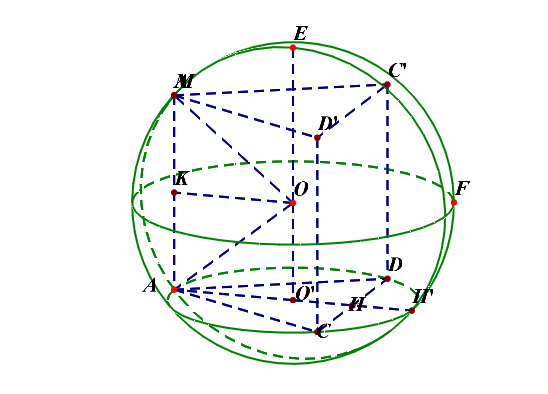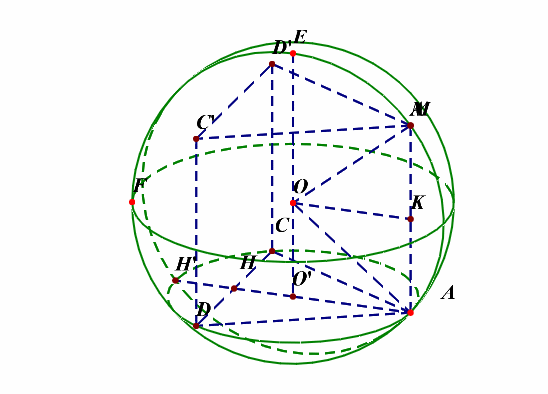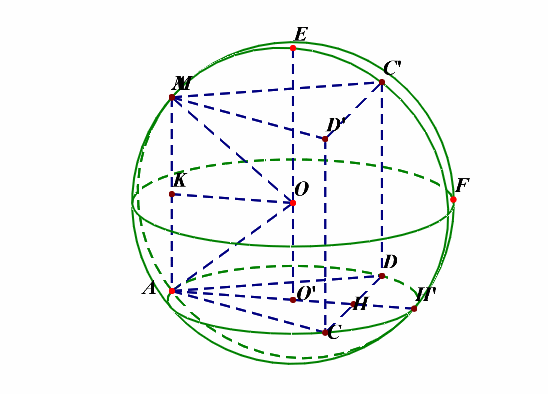
解后反思：当一条侧棱和下底面垂直时，常将三棱锥(M-ACD)补体成直三棱柱(MC'D'-ACD)，这样容易想清楚。

例17三棱锥(P-ABC)中，( riangle ABC)为等边三角形，(PA=PB=PC=3)，(PAperp PB)，则三棱锥(P-ABC)的外接球的表面积为__________。

分析：补体并特殊化为为正方体的一个角，如图所示，

则体对角线长为(3sqrt{3})，即(R=cfrac{3sqrt{3}}{2})，故(S_{表}=4pi R^2=27pi).