Levenshtein Distance,又称Edit Distance,在自然语言处理中有着广泛的应用。Levenshtein Distance 指的是两个字符串之间,由一个转换成另一个所需的最少编辑操作次数。编辑操作包括:1)删除一个字符;2)插入一个字符;3)替换一个字符
Example:
两个字符串a = "kitten", b = "ssitting",编辑过程如下:
- kitten → sitten (substitution of "s" for "k")
- sitten → sittin (substitution of "i" for "e")
- sittin → sitting (insertion of "g" at the end).
因此,a与b之间的编辑距离等于3。
解决方案:动态规划
1)描述最优解结构,寻找最优子结构
a = {x1, x2..xi}与字符串b = {y1, y2...yj}之间的最小编辑次数leva,b(i, j)。
- 如果xi = yj,leva,b(i, j) = leva,b(i-1, j-1)
- 如果xi ≠ yj,leva,b(i, j)将是以下三种情况中,编辑次数最少的一个
(1) 替换xi ,让xi 替换yj,编辑距离leva,b(i, j) = leva,b(i-1, j-1) + 1
(2) 在a中的第i个位置,插入新字符x让字符x = yj,leva,b(i, j) = leva,b(i, j-1) + 1
(3) 在a中的第i个位置, 删除入字符xi ,leva,b(i, j) = leva,b(i-1, j) + 1
2)递归定义最优解
有了上面的分析,递归表达式可以容易的推导出来:
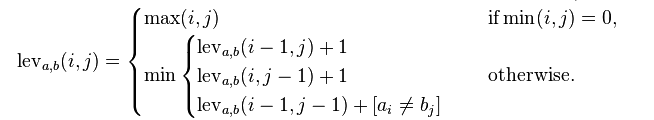
3)自底向上的实现
#include <iostream> using namespace std; /************************************************************************/ /* * a: 源字符串 * b: 目的字符串 * m: 源字符串长度 * n: 目的字符串的长度 /************************************************************************/ int lev_distance(const char* a, const char* b, int m, int n) { int* pre_col = new int[n+1]; int* cur_col = new int[n+1]; for (int i = 0; i != n+1; i++) { pre_col[i] = i; } for (int i = 0; i != m; i++) { cur_col[0] = i + 1; for (int j = 0; j < n; j++) { cur_col[j+1] = min(min(1 + cur_col[j], 1 + pre_col[j+1]), pre_col[j] + (a[i] == b[j] ? 0 : 1)); } swap(pre_col, cur_col); } return pre_col[n]; } int main() { char a[] = "kitten"; char b[] = "sitting"; int dist = lev_distance(a, b, sizeof(a)-1, sizeof(b)-1); cout<<"levenshtein distance:"<<dist<<endl; system("pause"); return 0; }
正常的动态规划算法需要记录表格大小是len(a) * len(b),当字符串长度较长的情况下,将需要很大的存储空间,上面的算法针对这种情况做了一个小的改进:lev(i, j)仅依赖于表格中的三个位置,左边,上方,左上方,因此只要保留当前列与左边一列就可以求出lev(i, j)的值了。