动态规划(dynamic programming)是一种高效的程序设计技术,一般应用与最优化问题,即当我们面临多组选择时,选择一个可行解让问题达到最优。动态规划的一个显著特点是:原问题可以划分成更小的子问题的最优化问题,而这些子问题的解往往有着重叠的部分。
动态规划算法的解决一个问题,可以分成四个步骤:
1)描述最优解结构,需找最优子结构
2)递归定义最优值的解
3)自底向上的求解问题
4)依据计算过程,构造一个最优解
1)与 2)是这个问题可以用动态规划解决的理论基础,3)可以看出是动态规划算法的编程实践,4)是算法输出,依赖于3)。下面分别用三个经典的动态规划案例,阐释动态规划算法的用法。
案例一:矩阵连乘
问题描述:给定n个矩阵{A1,A2,…,An},其中Ai与Ai+1是可乘的,i=1,2,…,n-1。考察这n个矩阵的连乘积A1A2…An。由于矩阵乘法满足结合律,故计算矩阵的连乘积可以有许多不同的计算次序,这种计算次序可以用加括号的方式来确定。若一个矩阵连乘积的计算次序完全确定,则可以依此次序反复调用2个矩阵相乘的标准算法计算出矩阵连乘积。若A是一个p×q矩阵,B是一个q×r矩阵,则计算其乘积C=AB的标准算法中,需要进行pqr次数乘。矩阵连乘积的计算次序不同,计算量也不同
Example:先考察3个矩阵{A1,A2,A3}连乘,设这三个矩阵的维数分别为10×100,100×5,5×50。
- 若按((A1A2)A3)方式需要的数乘次数为10×100×5+10×5×50=7500
- 若按(A1(A2A3))方式需要的数乘次数为100×5×50+10×100×50=75000。
解决方案:动态规划
1)描述最优解结构,寻找最优子结构
记AiAi+1…Aj为A[i:j],考察A[1:n]的最优计算次序问题:假设这个计算次序在k(1<=k<=n)处断开,那么A[1:k]和A[k+1:n]两个子序列的中的计算次序也是最优的。
为证明子结构与原问题也是一个相同的最优问题,一般采用反证法:
如果A[1:k]或者A[k+1:n]不是最优的,那么可以必然可以找到一个新的计算次序将A[1:k]或是A[k+1:n]替换,新的计算序列需要的计算次数更少,但这与A[1:n]是最有解序列矛盾。
2)递归定义最优值
令m[i][j]表示A[i:j]最小的计算次数,那么递归定义的表达式如下:

3)自底向上的求解
有了2)的递归表达式,,代码实现将会变得简单,代码如下:
/************************************************************************/ /* p: 输入参数,存储矩阵序列的中行列值 * m: m[i][j], 存放A[i:j]的计算次数 s: s[i][j], 记录A[i:j]断开的位置 */ /************************************************************************/ int matrix_chain(int* p, int n, int** m, int** s) { for (int i = 0; i != n; i++) { m[i][i] = 0; } for (int r = 2; r <= n; r++) { for (int i = 0; i <= n-r; i++) { int j = i + r - 1; m[i][j] = m[i+1][j] + p[i]*p[i+1]*p[j+1]; //从i处断开 s[i][j] = i; for (int k = i+1; k <= j; k++) { int t = m[i][k] +m[k+1][j] + p[i]*p[k+1]*p[j+1]; //从k处断开
if (t< m[i][j])
{
m[i][j] = t;
s[i][j] = k;
}
}
}
}
}
4)构造最优解
在第三步自底向上的求解过程中,记录了构建最优解的最优的必要形式(A[i:j]该断开的位置),构造最优解的过程如下:
void trace_back(int** s, int i, int j) { if (i == j) { return; } trace_back(s, i, s[i][j]); trace_back(s, s[i][j] + 1, j); cout<<"A("<<i<<","<<s[i][j]<<")"<<" "; cout<<"Multiply "<<"A("<<s[i][j]+1<<","<<j<<")"<<endl; }
程序的主函数如下:
int main() { const int n = 6; int p[] = {30, 35, 15, 5, 10, 20, 25}; int **m, **s; m = new int*[n]; for( int i = 0; i < n; i++) m[i] = new int[n]; s = new int*[n]; for(int i=0; i<n; i++) s[i] = new int[n]; matrix_chain(p, n, m, s); trace_back(s, 0, n-1); for(int i=0;i<n;i++) { delete []m[i]; delete []s[i]; } delete []m; delete []s; system("pause"); return 0; }
案例二:最长公共子序列
问题描述:子序列是指,在原序列中删除若干元素后所得的序列。公共子序列是指,给定两个序列X和Y,另一个序列Z既是X的子序列又是Y的子序列,那么Z则被称为X与Y的公共子序列。而最长公共子序列,则是求X与Y最长的子序列中长度最大的一个序列。
Example: X = {A,B, C, B, D, A, B}, Y = {B, D, C, A, B, A},他们的一个最长公共子序列是Z = {B, C, B, A }
解决方案:动态规划
步骤一:描述最优解结构,寻找最优子结构
设序列X = {x1, x2,....xn}, 序列Y = {y1, y2,...ym},它们的最长公共子序列是Z = {z1,z2, ...zk},他们之间有如下的最优结构性质:
1)若xn=ym,则zk=xn=ym,zk-1将是Xn-1与Yn-1的最长公共子序列
2)若xn=ym且zk≠xn,那么Z是Y与Xn-1最长公共子序列
3)若xn=ym且zk≠ym,那么Z是X与Yn-1最长公共子序列
有关最优子结构性质,依然可以采用反证法证明。
2)递归定义最优值
记c[i][j]表示序列Xi与序列Yj最长公共子序列的长度,其中Xi = {x1, x2,....xi}, Yj = {y1, y2,...yj},有如下的递归定义表达式:

3)自底向上的求解
依照上面的公式,自底向上的求解代码的代码如下:
#include <iostream> using namespace std; int lcs_length(char* x, int m, char* y, int n, int** c) { for (int i = 0; i <= m ; i++) c[i][0] = 0; for (int j = 0; j <= n; j++) c[0][j] = 0; for (int i = 1; i <=m; i++) { for (int j = 1; j <= n; j++) { if (x[i-1] == y[j-1]) //下标从l开始 { c[i][j] = c[i-1][j-1] + 1; } else { c[i][j] = max(c[i-1][j], c[i][j-1]); } } } return c[m][n]; } void print_lcs(int i, int j, char* x, int** c) { if (i == 0 || j == 0) { return; } if (c[i][j] == c[i-1][j-1] + 1) { print_lcs(i-1, j-1, x, c); cout<<x[i-1]<<endl; } else if (c[i][j] == c[i-1][j]) { print_lcs(i-1, j, x, c); } else { print_lcs(i, j-1, x, c); } } int main() { char x[] = {"ABCBDAB"}; char y[] = {"BDCABA"}; int m = strlen(x); int n = strlen(y); int** c = new int*[m+1]; for (int i = 0; i<=m; i++ ) { c[i] = new int[n+1]; } int t = lcs_length(x, m, y, n, c); for (int i = 0; i <= m; i++) { for (int j = 0; j <= n; j++) { cout<<c[i][j]<< " "; } cout<<endl; } print_lcs(m, n, x, c); system("pause"); return 0; }
代码的执行图解如下:
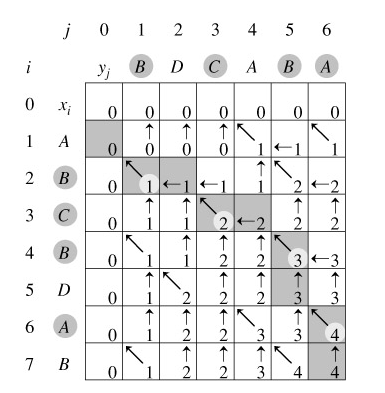
案例三:最长递增子序列
问题描述:求一个一维数组(N个元素)中的最长递增子序列的长度。
Example:在序列1,-1,2,-3,4,-5,6,-7中,其最长的递增子序列为1,2,4,6。
解决方案:动态规划
继续依据动态规划的解决思想,解决过程省略,这里直接给出最优解的递归结构表达式,令m(i, j)表示以i为起点j为终点(包括原始array[i])的子序列,增长序列的最长长度,则递归表达式为:

实现代码如下:
#include <iostream> using namespace std; /************************************************************************/ /* array: 存放序列 m: m[i][j],表示以i为起点j为终点(包括原始array[i])的子序列,增长序列长度 n: array长度 */ /************************************************************************/ int lis_length(int* array, int** m, int n) { for (int i = 0; i < n; i++) { m[i][i] = 1; } for (int r = 2; r <= n; r++) { for (int i = 0; i <= n - r; i++) { int j = i + r -1; if (array[i] < array[i+1]) { m[i][j] = m[i+1][j] + 1; } else { m[i][j] = m[i+1][j]; } } } return m[0][n-1]; } void print_lis(int* array, int** m, int n) { int lic_len = m[0][n-1]; //m[0][i]记录了序列array[0:i],最长递增长度 //m[0][i] = k,序列第k个增长元素出现 for (int i = 0, lic_tag = 1; i != n; i++) { if (m[0][i] == lic_tag) { cout<<array[i]<<" "; lic_tag += 1; } } } int main() { const int n = 8; int array[n] = {1, 4, 2, -3, 4, 8, 6, -7}; int** m = new int*[n]; for (int i = 0; i != n; i++) { m[i] = new int[n]; } int t = lis_length(array, m, n); print_lis(array, m, n-1); for (int i = 0; i != n; i++) { delete[] m[i]; } delete[] m; system("pause"); return 0; }
总结:1)能够最优子结构性质,是使用动态规划算法的先决条件;2)重复解结构,动态规划算法能够高效使用的原因在于记录了子结构的解,而这些解又会在后续的求解过程中被我们使用(优于递归算法的原因);3)最后在编程实践技巧上,利用了自底向上的求解技术,从子问题开始求解。
在编程实践的过程,特别需要主要以下问题:1)初始化,零界情况下表格的初始化必须提前完成;2)子问题的求解一定要现优于原问题,如出现某个子问题未求解出,但算法开始处理该原问题,将会引入错误(错误将非常隐晦);3)解的信息保存。