参考:
https://zhuanlan.zhihu.com/p/36229547
https://www.cnblogs.com/-citywall123/p/11322771.html
https://blog.csdn.net/Patrickpwq/article/details/80210847
https://blog.csdn.net/weixin_43701790/article/details/107896562
https://blog.csdn.net/weixin_42165786/article/details/89221150
最大流问题很直观,但处理起来真的不简单,不仅要搞清楚最大流最小割定理,而且对增广路径的寻找也要基于原有的图遍历算法进行修改才能使用。
反向边的问题,是为了解决贪婪算法的局限性,给程序一个反悔的机会,但并不是很好理解!
先上个图,这个图实从网上来的,根应该在算法导论。
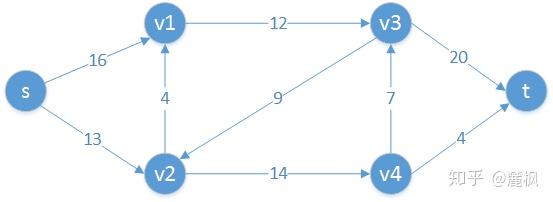
一、构造一个图
/** * 总结对于一个图而言,一个好的数据结构应该有哪些特征: * 1.顶点本身可以有名称,也应该可以弹性增加各种属性 * 2.通过边结构,从一个顶点可以很容易的找到它所连接的其他顶点 * 3.可以方便的增加删除顶点和边 * 4.边至少应该有权重属性 * 5.如果以后边需要存储更多信息,可以考虑将Table的value更新为一个Edge对象 */ @Data @AllArgsConstructor @NoArgsConstructor public class Graph7 { //如果不需要顶点的索引,那set比list更方便 private Set<Node> nodeList; private Table<Node, Node, Edge> edgeTable; @Data @AllArgsConstructor @NoArgsConstructor static class Node { private String name; private boolean visit; private boolean deadEnd; public Node(String name) { this.name = name; } @Override public boolean equals(Object o) { if (this == o) return true; if (o == null || getClass() != o.getClass()) return false; Node node = (Node) o; return name.equals(node.name); } @Override public int hashCode() { return Objects.hash(name); } @Override public String toString() { return "Node{" + "name='" + name + '\'' + '}'; } } @Data @AllArgsConstructor @NoArgsConstructor static class Edge{ //权重 private Integer weight; //容量/剩余容量 private Integer c; public Edge(Integer c) { this.c = c; } @Override public String toString() { return "Edge{" + "c=" + c + '}'; } } /** * 根据顶点名称获取顶点 * * @param nodeList * @param name * @return */ public static Node getNode(Set<Node> nodeList, String name) { for (Node node : nodeList) { if (node.getName().equals(name)) { return node; } } return null; } /** * 从图中删除一个顶点,关联的也需要删除 * * @param node */ public void remove(Node node) { ArrayList<Pair<Node, Node>> pairs = Lists.newArrayList(); for (Table.Cell<Node, Node, Edge> cell : edgeTable.cellSet()) { if (cell.getRowKey().equals(node) || cell.getColumnKey().equals(node)) { pairs.add(new Pair<>(cell.getRowKey(), cell.getColumnKey())); } } for (Pair<Node, Node> pair : pairs) { edgeTable.remove(pair.getFrom(), pair.getTo()); } nodeList.remove(node); } public static Graph7 buildGraph() { List<String> nodes = Lists.newArrayList("C","A", "B", "D"); List<String> hop = Lists.newArrayList( "C->B", "A->D","D->C","A->C"); Set<Node> nodeList = nodes.stream().map(Node::new).collect(Collectors.toSet()); HashBasedTable<Node, Node, Edge> table = HashBasedTable.create(); for (String s : hop) { String[] split = s.split("->"); String from = split[0]; String to = split[1]; Node fromNode = getNode(nodeList, from); Node toNode = getNode(nodeList, to); table.put(fromNode, toNode, new Edge()); } return new Graph7(nodeList, table); } /** * 获取一个图的入度 * @param graph7 * @return */ public Map<Node,Integer> getInDegree(Graph7 graph7) { HashMap<Node, Integer> map = new HashMap<>(); Set<Node> nodeList = graph7.getNodeList(); Table<Node, Node, Edge> edgeTable = graph7.edgeTable; for (Node node : nodeList) { map.put(node,0); } for (Table.Cell<Node, Node, Edge> cell : edgeTable.cellSet()) { map.computeIfPresent(cell.getColumnKey(),(k, v) -> v + 1); } return map; } /** * 图的拓扑排序 * @param graph7 */ public void findPriority(Graph7 graph7) { Map<Node, Integer> inDegree = getInDegree(graph7); while (graph7.nodeList.size()!=0) { System.out.println(inDegree); for (Map.Entry<Node, Integer> entry : inDegree.entrySet()) { if (entry.getValue().equals(0)) { System.out.println(entry.getKey()); graph7.remove(entry.getKey()); } } inDegree=getInDegree(graph7); } } public static void main(String[] args) { Graph7 graph7 = buildGraph(); // graph7.bfs(graph7,new Node("C")); System.out.println("=================="); graph7.dfs(graph7); } /** * 广度优先遍历 * @param graph7 * @param head */ public void bfs(Graph7 graph7, Node head) { Table<Node, Node, Edge> edgeTable = graph7.getEdgeTable(); Queue<Node> queue = new LinkedList<>(); head.setVisit(true); System.out.println(head); //加入队列的都已经访问了 queue.add(head); while (!queue.isEmpty()) { Node remove = queue.remove(); Map<Node, Edge> rowMap = edgeTable.row(remove); for (Node node : rowMap.keySet()) { if (!node.visit) { node.visit=true; System.out.println(node); queue.add(node); } } } } /** * 深度优先遍历 * @param graph7 */ public void dfs(Graph7 graph7) { Set<Node> nodeList = graph7.getNodeList(); Table<Node, Node, Edge> edgeTable = graph7.getEdgeTable(); for (Node node : nodeList) { node.visit=false; } for (Node node : nodeList) { if (!node.visit) { doDfs(edgeTable,node); } } } private void doDfs(Table<Node, Node, Edge> edgeTable,Node node) { node.visit=true; System.out.println(node); Map<Node, Edge> rowMap = edgeTable.row(node); for (Node node1 : rowMap.keySet()) { if (!node1.visit) { doDfs(edgeTable, node1); } } } }
二、寻找增广路径
增广路径的难点在于他既不是广度优先遍历,也不是深度优先遍历,而是类似于一个迷宫问题。
我是基于深度优先遍历写的。但深度优先会有一个死路问题,程序需要在遇到死胡同的时候自己退出来。
这就用到了stack这个数据结构。但stack只是存储了节点的顺序,因为我们还需要路径的容量,所以用了另外一个table结构来存储最终的结果。
在最后的时候,肯定有一种已经找不到新的增广路径的情况这个时候需要能够及时退出程序。
跟普通的遍历不同,这里的节点可以有三种状态:1.没有访问,2.访问过(拒绝环图的死循环),3.访问过,而且确定是死路
/** * 残存网络里残存的是什么?容量还是流量? * 容量! * 如何找到增广路径,深度优先遍历! * 1.深度优先,有两种可能,一路找下去找到了,循环结束 * 2.到了某个节点,他没有有效路径了,则将它设置为已访问,然后回退到上个节点,这个时候需要stack * 3.stack弹出栈顶元素,一直回退,直到所有节点都访问了,就退出循环 * * @param graph7 */ public static Table<Graph7.Node, Graph7.Node, Integer> findPath(Graph7 graph7) { System.out.println("========================findPath========================"); Table<Graph7.Node, Graph7.Node, Integer> result = HashBasedTable.create(); Set<Graph7.Node> nodeList = graph7.getNodeList(); //每次访问前把标志设false nodeList.forEach(node -> node.setVisit(false)); Table<Graph7.Node, Graph7.Node, Graph7.Edge> edgeTable = graph7.getEdgeTable(); Graph7.Node head = Graph7.getNode(nodeList, "s"); Graph7.Node end = Graph7.getNode(nodeList, "t"); //用stack来存储增广路径 Stack<Graph7.Node> stack = new Stack<>(); stack.push(head); assert head != null; head.setVisit(true); System.out.println(head); boolean isSuccess = false; //找到了,就跳出外层循环 outLoop: while (!stack.isEmpty()) { //拿到栈顶元素,但不删除 Graph7.Node node = stack.peek(); Map<Graph7.Node, Graph7.Edge> rowMap = edgeTable.row(node); boolean hasNext = false; //如果一个节点所有指向的节点都不能找到一条有效边,则设这个节点是访问过的,以后不需要再访问 for (Graph7.Node node1 : rowMap.keySet()) { Graph7.Edge edge = edgeTable.get(node, node1); //找到一条有效路径 if (!node1.isVisit() && edge != null && edge.getC() > 0) { System.out.println(node1); node1.setVisit(true); hasNext = true; stack.push(node1); if (node1.equals(end)) { isSuccess = true; break outLoop; } //退出内层循环 break; } } //遍历了所有下游节点,但没找到出路,这个节点就不用再访问了 if (!hasNext) { node.setDeadEnd(true); stack.pop(); } } System.out.println("isSuccess:" + isSuccess); if (!isSuccess) { result.clear(); } else { Graph7.Node next = stack.pop(); while (!stack.isEmpty()) { Graph7.Node node = stack.pop(); Integer c = edgeTable.get(node, next).getC(); result.put(node, next, c); next = node; } } return result; }
三、寻找最大流
寻找最大流的关键除了前面的寻找增广路径外,另外一个就是残存网络的更新。
残存网络的更新在正向边上没有什么可以说的,就是容量-流量,但反向边是比较难理解的。
其实并不是简单正向容量减反向容量加,更不是正向加反向减
public static Integer findMaxFlow(Graph7 graph7) { Set<Graph7.Node> nodeList = graph7.getNodeList(); Table<Graph7.Node, Graph7.Node, Graph7.Edge> edgeTable = graph7.getEdgeTable(); //构造一个新的残存网络,一开始跟原图一样 Graph7 residualGraph = new Graph7(); HashBasedTable<Graph7.Node, Graph7.Node, Graph7.Edge> residualTable = HashBasedTable.create(); for (Table.Cell<Graph7.Node, Graph7.Node, Graph7.Edge> edgeCell : edgeTable.cellSet()) { Graph7.Node rowKey = edgeCell.getRowKey(); Graph7.Node columnKey = edgeCell.getColumnKey(); Integer originC = edgeCell.getValue().getC(); //正向边容量初始化 Graph7.Edge positiveEdge = new Graph7.Edge(originC); residualTable.put(rowKey, columnKey, positiveEdge); } residualGraph.setNodeList(nodeList); residualGraph.setEdgeTable(residualTable); int maxFlow = 0; //增广路径 Table<Graph7.Node, Graph7.Node, Integer> augmentPath = findPath(residualGraph); while (augmentPath.size() != 0) { //在增广路径中找到最小流量 int m = augmentPath.cellSet().stream().mapToInt(Table.Cell::getValue).min().getAsInt(); System.out.println("newFlow=" + m); for (Table.Cell<Graph7.Node, Graph7.Node, Integer> cell : augmentPath.cellSet()) { Graph7.Node rowKey = cell.getRowKey(); Graph7.Node columnKey = cell.getColumnKey(); //如果路径的边原来是存在的,边上的容量等于原来的容量-发现的最小容量 if (edgeTable.contains(rowKey, columnKey)) { //正向容量 Integer c = residualGraph.getEdgeTable().get(rowKey, columnKey).getC(); residualGraph.getEdgeTable().get(rowKey, columnKey).setC(c - m); //反向加流量 Graph7.Edge reverseEdge = residualGraph.getEdgeTable().get(columnKey, rowKey); if (reverseEdge == null) { residualGraph.getEdgeTable().put(columnKey, rowKey, new Graph7.Edge(m)); } else { Integer oldC1 = reverseEdge.getC(); reverseEdge.setC(oldC1 + m); } } else {//rc是反向,那么cr肯定是正向的 //不是简单正向加反向减,也不是反向加正向减,而是当前被用的的要被减,没被用的加 Graph7.Edge edge = residualGraph.getEdgeTable().get(columnKey, rowKey); Integer oldC2 = edge.getC(); edge.setC(oldC2 + m); //反向被用掉了,所以要减流量 Graph7.Edge reverseEdge = residualGraph.getEdgeTable().get(rowKey, columnKey); if (reverseEdge == null) { //一开始肯定是没有反向边的,所以需要做个判断 residualGraph.getEdgeTable().put(rowKey, columnKey, new Graph7.Edge(m)); } else { Integer oldC3 = reverseEdge.getC(); residualGraph.getEdgeTable().get(rowKey, columnKey).setC(oldC3 - m); } } } maxFlow = maxFlow + m; augmentPath = findPath(residualGraph); } return maxFlow; }
这个图的最大流是23