java实现最小生成树

最小生成树有两个算法Kruskal算法和prime算法
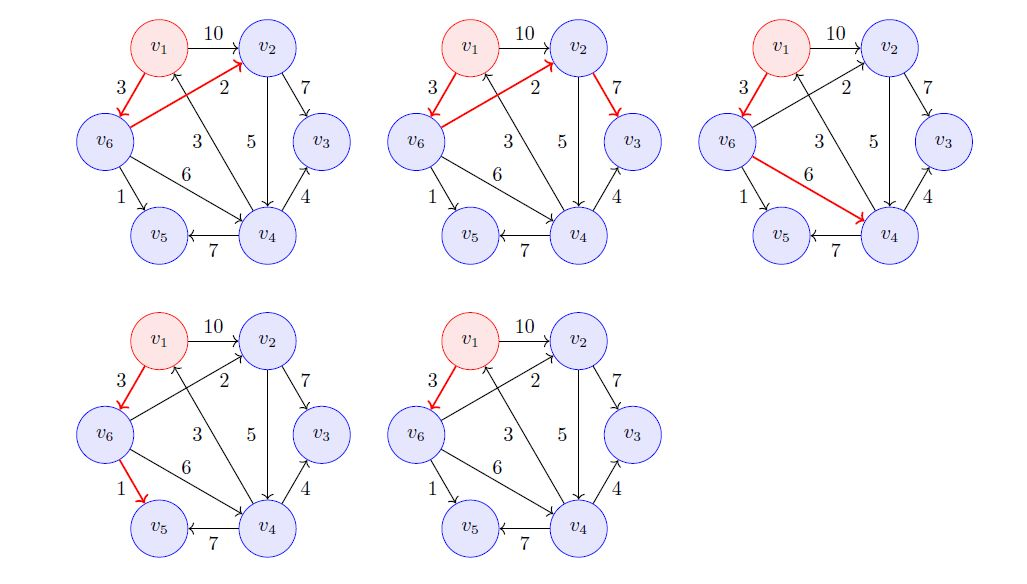
还是借用上一篇的图

public class MinimalTree {
    public static void main(String[] args) {
        WeightGraph weightGraph = buildGraph();
        List<WeightEdge<String, String, Integer>> weightEdges = buildKruskalTree(weightGraph);
        System.out.println("tree:");
        for (WeightEdge<String, String, Integer> weightEdge : weightEdges) {
            System.out.println(weightEdge);
        }

        List<WeightEdge<String, String, Integer>> weightEdges1 = buildPrimeTree(weightGraph);
        System.out.println("prime:");
        for (WeightEdge<String, String, Integer> weightEdge : weightEdges1) {
            System.out.println(weightEdge);
        }


    }

    /**
     * 最小生成树之prime算法
     * 基本思路：
     * 1.从图的所有顶点随机取出一个node,加入已知集合U，那其他节点加入未知集合V，U+V=所有节点
     * 2.遍历所有已知边，找到U和V之间最短的一条，加入结果边集，同时将此边联通的未知节点从V中移动到U
     * 3.继续循环，指定V的集合为空
     *
     * @param weightGraph
     * @return
     */
    public static List<WeightEdge<String, String, Integer>> buildPrimeTree(WeightGraph weightGraph) {
        List<String> nodes = weightGraph.getNodes();
        List<WeightEdge<String, String, Integer>> edgeList = weightGraph.getEdgeList();
        //结果list
        List<WeightEdge<String, String, Integer>> miniEdges = Lists.newArrayList();
        //初始节点
        String s = nodes.get(0);
        //初始化已知集合和未知集合
        Set<String> knowSet = Sets.newHashSet(s);
        Set<String> notKnowSet = Sets.newHashSet();
        for (String node : nodes) {
            if (!knowSet.contains(node)) {
                notKnowSet.add(node);
            }
        }
        while (!notKnowSet.isEmpty()) {
            WeightEdge<String, String, Integer> miniEdge = null;
            Integer shortest = Integer.MAX_VALUE;
            String newNode = null;
            for (WeightEdge<String, String, Integer> edge : edgeList) {
                String start = edge.getStart();
                String end = edge.getEnd();
                Integer weight = edge.getWeight();
                if ((knowSet.contains(start) && notKnowSet.contains(end)) || (knowSet.contains(end) && notKnowSet.contains(start))) {
                    if (weight < shortest) {
                        shortest = weight;
                        miniEdge = edge;
                        if (knowSet.contains(start)) {
                            newNode = end;
                        } else {
                            newNode = start;
                        }
                    }
                }
            }
            //更新结果边集合
            miniEdges.add(miniEdge);
            //更新已知节点和未知节点集合
            knowSet.add(newNode);
            notKnowSet.remove(newNode);
        }
        return miniEdges;
    }

    /**
     * 最小生成树之Kruskal算法
     * 基本逻辑：
     * 1.将所有边加入到一个以边长作为优先要素的优先队列
     * 2.初始化最小生成树的边数count为0，从优先队列取出一条边，判断边的两个端点是否连通
     * 3.如果不连通，则将这条边加入到生成树的边集合，且count=count+1,
     * （如果两个节点已经联通，则再加就会构成环路，就不是最小生成树了）
     * 4.继续循环，知道count的数量=顶点数-1
     * @param weightGraph
     * @return
     */
    public static List<WeightEdge<String, String, Integer>> buildKruskalTree(WeightGraph weightGraph) {
        List<String> nodes = weightGraph.getNodes();
        int size = nodes.size();
        List<WeightEdge<String, String, Integer>> edgeList = weightGraph.getEdgeList();
        List<WeightEdge<String, String, Integer>> miniEdges = Lists.newArrayList();
        //构造以权重为优先级的优先队列，这样可以方便从头部获取最短边
        PriorityQueue<WeightEdge<String, String, Integer>> priorityQueue = new PriorityQueue<>(Comparator.comparing(WeightEdge::getWeight));
        priorityQueue.addAll(edgeList);
        int count = 0;
        //最小生成树的边一定等于顶点数-1
        while (count < size - 1) {
            WeightEdge<String, String, Integer> edge = priorityQueue.remove();
            String start = edge.getStart();
            String end = edge.getEnd();
            //如果start和end之前就不联通，则加入
            if (!isLink(miniEdges, start, end)) {
                miniEdges.add(edge);
                count += 1;
            }
        }

        return miniEdges;
    }

    /**
     * 判断两个节点是否是联通的
     * 最初的联通图是一个空map,说明没有节点是联通的
     * 所以联通的条件是两个节点都在连通图中，且key相同
     *
     * @param node1
     * @param node2
     * @return
     */
    public static boolean isLink(List<WeightEdge<String, String, Integer>> miniEdges, String node1, String node2) {
        System.out.println("linkMap:");
        Multimap<String, String> linkMap = getLinkMap(miniEdges);
        System.out.println(linkMap);
        if (linkMap.containsValue(node1) && linkMap.containsValue(node2)) {
            String k1 = getKeyByValue(linkMap, node1);
            String k2 = getKeyByValue(linkMap, node2);
            if (k1.equals(k2)) {
                return true;
            }
        }
        return false;
    }

    /**
     * 通过图的边构造图的联通map,所有联通的节点放在一个key的value中
     *
     * @param miniEdges
     * @return
     */
    public static Multimap<String, String> getLinkMap(List<WeightEdge<String, String, Integer>> miniEdges) {
        Multimap<String, String> map = HashMultimap.create();

        for (WeightEdge<String, String, Integer> s : miniEdges) {
            String from = s.getStart();
            String to = s.getEnd();
            //默认from、to都不存在
            boolean fromPresent = false;
            boolean toPresent = false;
            if (isPresent(map, from)) {
                fromPresent = true;
            }
            if (isPresent(map, to)) {
                toPresent = true;
            }
            //from/to都不存在，最简单,from做key,将from和to放value里
            if (!fromPresent && !toPresent) {
                map.put(from, from);
                map.put(from, to);
                //from存在，to不存在，要区分from是key还是value
            } else if (!toPresent) {
                boolean inKey = map.containsKey(from);
                if (inKey) {
                    map.put(from, to);
                } else {
                    String valKey = getKeyByValue(map, from);
                    map.put(valKey, to);
                }
                //to存在，from不存在，也要区分to是key还是value
            } else if (!fromPresent) {
                boolean toInKey = map.containsKey(to);
                if (toInKey) {
                    map.put(to, from);
                } else {
                    String valKey = getKeyByValue(map, to);
                    map.put(valKey, from);
                }
            }
            //剩下最后一种可能，from/to都存在，那就不需要处理了
        }

        return map;

    }

    /**
     * 判断一个元素是否存在于map中，需要判断两种情况
     *
     * @param map
     * @param key
     * @return
     */
    public static boolean isPresent(Multimap<String, String> map, String key) {
        return map.containsKey(key) || map.containsValue(key);
    }

    /**
     * 从map中反向查找value对应的key，前提条件是value存在于map中
     *
     * @param map
     * @param val
     * @return
     */
    public static String getKeyByValue(Multimap<String, String> map, String val) {
        Set<String> keySet = map.keySet();
        for (String s : keySet) {
            Collection<String> values = map.get(s);
            if (values.contains(val)) {
                return s;
            }
        }
        return null;
    }


}

两个算法的输出是一样的：

tree:
WeightGraph.WeightEdge(start=v6, end=v5, weight=1)
WeightGraph.WeightEdge(start=v6, end=v2, weight=2)
WeightGraph.WeightEdge(start=v4, end=v1, weight=3)
WeightGraph.WeightEdge(start=v1, end=v6, weight=3)
WeightGraph.WeightEdge(start=v4, end=v3, weight=4)
prime:
WeightGraph.WeightEdge(start=v1, end=v6, weight=3)
WeightGraph.WeightEdge(start=v6, end=v5, weight=1)
WeightGraph.WeightEdge(start=v6, end=v2, weight=2)
WeightGraph.WeightEdge(start=v4, end=v1, weight=3)
WeightGraph.WeightEdge(start=v4, end=v3, weight=4)