Java实现最短路径算法（Dijkstra 算法）

参考：

https://zhuanlan.zhihu.com/p/129373740

《数据结构与算法-python描述》作者:裘宗燕

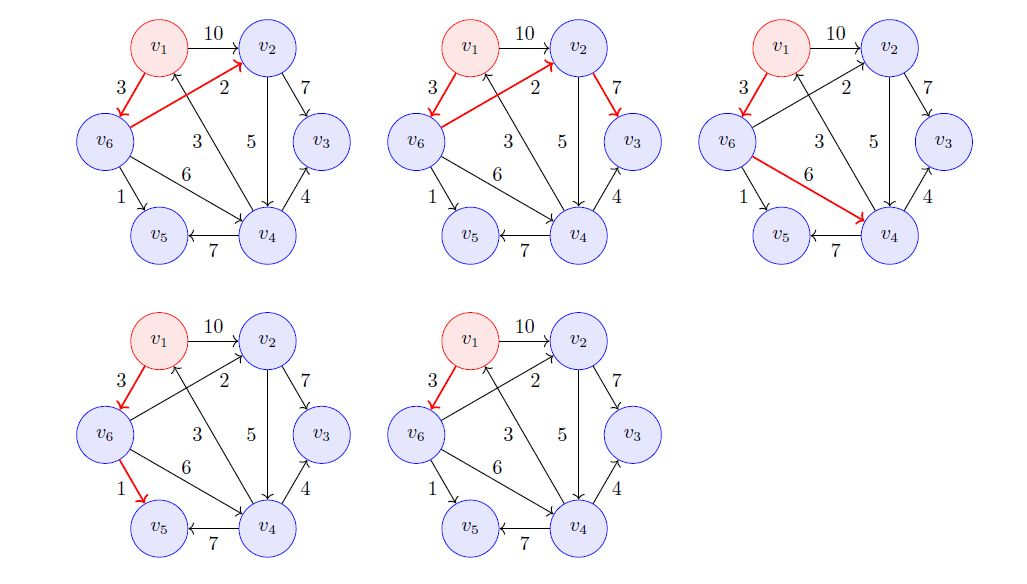
 以上是原图，求V1到其余所有节点的最短路径。参考了裘宗燕教授的数据结构与算法

并未完全理解其精髓，暂且记录，后面再慢慢理解

@Data
@AllArgsConstructor
public class WeightGraph {
    private List<String> nodes;
    private List<WeightEdge<String, String, Integer>> edgeList;


    public static void main(String[] args) {
        WeightGraph weightGraph = buildGraph();
        Map<String, Path<String, Integer>> shortest = findShortest(weightGraph);
        for (Map.Entry<String, Path<String, Integer>> entry : shortest.entrySet()) {
            System.out.println(entry.getKey() + ":" + entry.getValue().getLen());
        }
    }


    /**
     * 初始化图结构
     *
     * @return
     */
    public static WeightGraph buildGraph() {
        List<String> node = Lists.newArrayList("v1", "v2", "v3", "v4", "v5", "v6");
        List<WeightEdge<String, String, Integer>> edge = Lists.newArrayList();
        edge.add(new WeightEdge<>("v1", "v2", 10));
        edge.add(new WeightEdge<>("v2", "v3", 7));
        edge.add(new WeightEdge<>("v4", "v3", 4));
        edge.add(new WeightEdge<>("v4", "v5", 7));
        edge.add(new WeightEdge<>("v6", "v5", 1));
        edge.add(new WeightEdge<>("v1", "v6", 3));
        edge.add(new WeightEdge<>("v6", "v2", 2));
        edge.add(new WeightEdge<>("v4", "v1", 3));
        edge.add(new WeightEdge<>("v2", "v4", 5));
        edge.add(new WeightEdge<>("v6", "v4", 6));

        return new WeightGraph(node, edge);
    }


    public static Map<String, Path<String, Integer>> findShortest(WeightGraph weightGraph) {
        List<WeightEdge<String, String, Integer>> edgeList = weightGraph.getEdgeList();
        List<String> nodes = weightGraph.getNodes();
        //以路径边长做key的优先级队列
        PriorityQueue<Triple<Integer, String, String>> queue = new PriorityQueue<>(Comparator.comparing(Triple::getLen));
        //初始化队列
        //表示原点v1,经中间节点v1,到v1的距离是0
        queue.add(new Triple<>(0, "v1", "v1"));
        //结果map
        Map<String, Path<String, Integer>> paths = new HashMap<>();
        //paths初始为null，用于存储最终结果
        int size = nodes.size();
        for (String node : nodes) {
            paths.put(node, null);
        }

        int count = 0;
        while (count < size && !queue.isEmpty()) {
            //长度、中介、终点
            Triple<Integer, String, String> triple = queue.remove();
            String end = triple.getEnd();
            //如果end已经找到，则跳过本次循环
            if (paths.get(end) != null) {
                continue;
            }
            //如果end还为找到最短路径
            Integer len = triple.getLen();
            //因为从优先队列头部取出，因此<end,len>就是当前已知的最短路径
            //第一次执行("v1",new Path("v1",0)),v1经v1到v1的最短距离是0
            paths.put(end, new Path<>(triple.getMiddle(), len));
            //遍历所有以新得到的最短路径节点做start的边，扩展可达的边界
            for (WeightEdge<String, String, Integer> edge : edgeList) {
                if (edge.getStart().equals(end)) {
                    String newEnd = edge.getEnd();
                    Integer w = edge.getWeight();
                    //如果新目标还未确定最短路径，则将end做中介，原end的len+weight作为新的len,并加入优先queue
                    //优先队列保证经过这轮循环，得到了最新的最短路径节点
                    if (paths.get(newEnd) == null) {
                        queue.add(new Triple<>(len + w, end, newEnd));
                    }
                }
            }
            count += 1;
        }
        return paths;
    }
}

/**
 * 带权重的边
 *
 * @param <S>
 * @param <E>
 * @param <W>
 */
@Data
@AllArgsConstructor
@NoArgsConstructor
class WeightEdge<S, E, W> {
    private S start;
    private E end;
    private W weight;


}

/**
 * 优先队列元素三元组，主要用于获取目标节点的最短路径
 *
 * @param <L> length
 * @param <M> 中介点
 * @param <E> 目标点
 */
@Data
@AllArgsConstructor
class Triple<L, M, E> {
    private L len;
    private M middle;
    private E end;
}

/**
 * paths的元素格式
 *
 * @param <M> 中介点
 * @param <L> 最终最短路径
 */
@Data
@AllArgsConstructor
class Path<M, L> {
    private M middle;
    private L len;
}

输出：

v6:3
v1:0
v2:5
v3:12
v4:9
v5:4