matplotlib可视化系列之【坐标系统】

了解 matplotlib 的坐标系统，绘制图形的时候，如果需要在图上添加一些额外的元素或者说明文字，
就可以很好的控制添加元素和说明文字的位置。

笛卡尔坐标系和极坐标系

matplotlib 使用2种坐标系，笛卡尔坐标系是默认的，一般我们绘制的二维图形基本都是笛卡尔坐标系的。
比如各种柱状图，折线图，散点图等等。

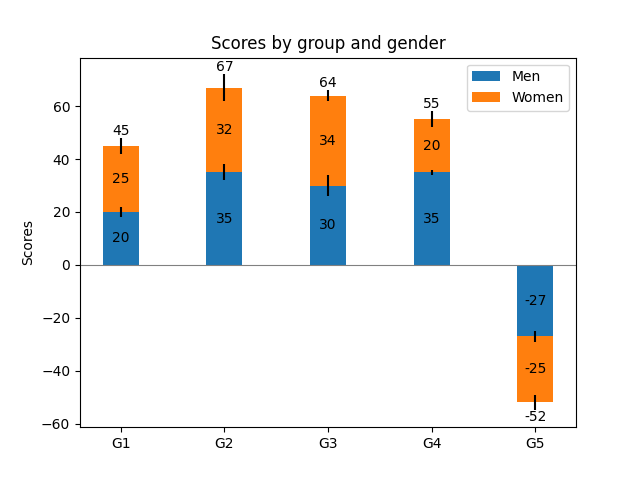
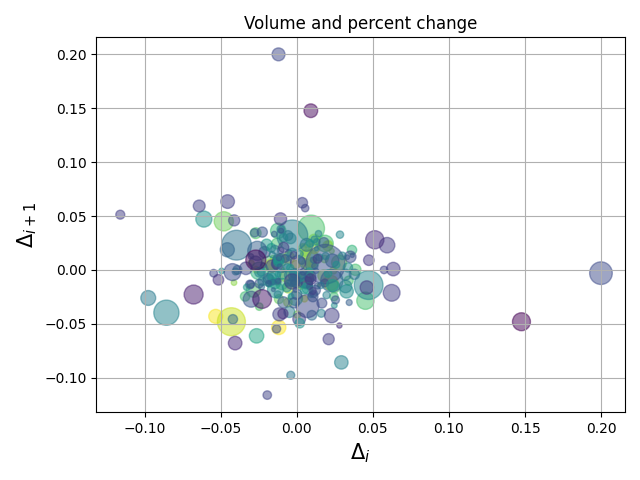
但是，有些场景下，极坐标能更好的展示分析的结果。
比如上面笛卡尔坐标系下的柱状图，折线图和散点图在极坐标系下显示效果类似：

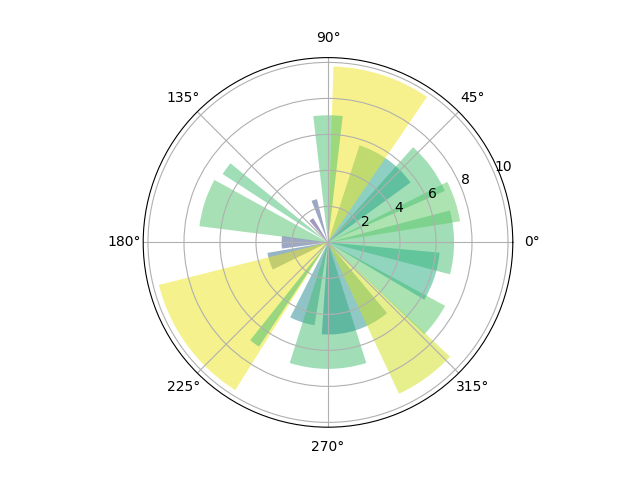
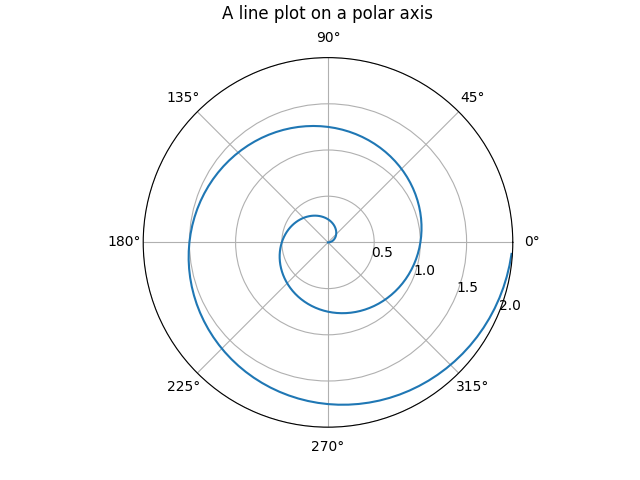
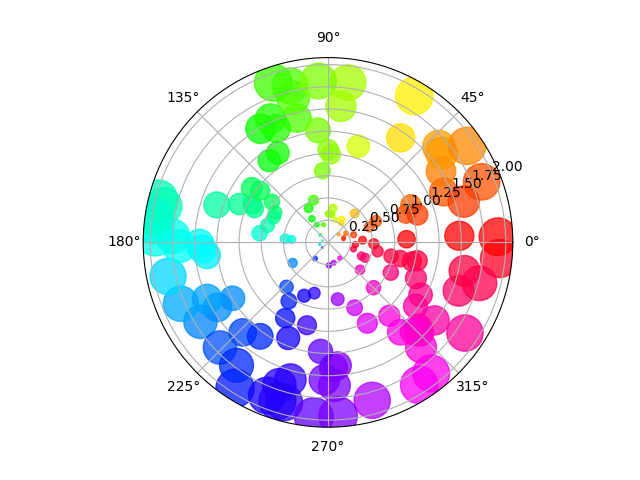
两种坐标系没有高低之分，根据场景选择合适的去展示。

图形中的坐标系

笛卡尔坐标系和极坐标系是宏观上的坐标系统，对于每个具体的图形，matplotlib 为了更好的在图形上绘制各种元素，
基于笛卡尔坐标系或者极坐标系，定义了绘制图形的4个坐标系：

1. FC：Figure coordinates，单位是像素
2. DC：Data coordinates，单位与显示数据的单位相同
3. NFC：标准化的 FC，数据范围 （0->1）
4. NDC：标准化的 DC，数据范围 （0->1）

在笛卡尔坐标系下：

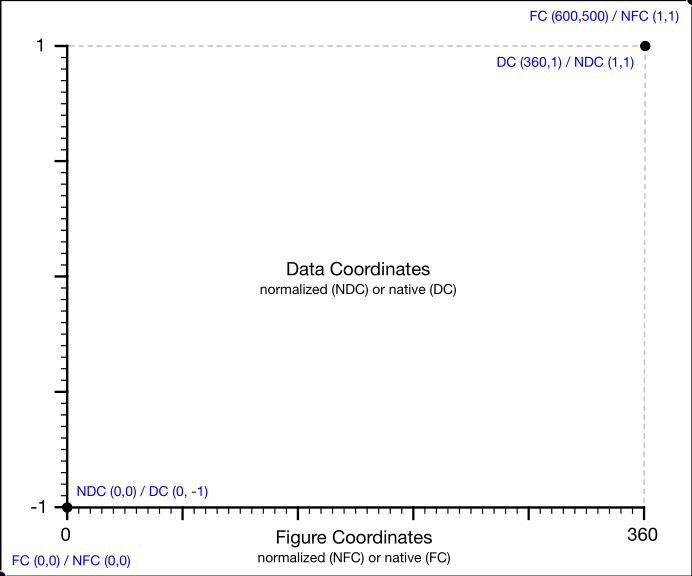
在极坐标系下：

图形中坐标系之间的转换

matplotlib 提供了接口，可以在4种坐标系之间的坐标是可以互相转换的。
​

对于如下的示例图形，提供的6种坐标系之间的转换接口如下：

fig = plt.figure(figsize=(6, 5), dpi=100)
ax = fig.add_subplot(1, 1, 1)
ax.set_xlim(0,360), ax.set_ylim(-1,1)

转换方向	转换方法
DC_to_FC	ax.transData.transform
FC_to_DC	ax.transData.inverted().transform
NDC_to_FC	ax.transAxes.transform
FC_to_NDC	ax.transAxes.inverted().transform
NFC_to_FC	fig.transFigure.transform
FC_to_NFC	fig.transFigure.inverted().transform

一共4种坐标系，如果两两之间都可以互相转换，应该有12种情况，这里却只有6种情况。
这是因为其他的情况可以由上面这6种接口推导出来，比如：

1. DC_to_NDC = FC_to_NDC(DC_to_FC)
2. DC_to_NFC = FC_to_NFC(DC_to_FC)
3. ... ... 等等

​

下面，用github上一段开源代码示例看看转换的结果：

# ----------------------------------------------------------------------------
# Title:   Scientific Visualisation - Python & Matplotlib
# Author:  Nicolas P. Rougier
# License: BSD
# ----------------------------------------------------------------------------
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.transforms as transforms

fig = plt.figure(figsize=(6, 5), dpi=100)
ax = fig.add_subplot(1, 1, 1)

ax.set_xlim(0, 360)
ax.set_ylim(-1, 1)

DC_to_FC = ax.transData.transform
FC_to_DC = ax.transData.inverted().transform

NDC_to_FC = ax.transAxes.transform
FC_to_NDC = ax.transAxes.inverted().transform

NFC_to_FC = fig.transFigure.transform
FC_to_NFC = fig.transFigure.inverted().transform


print(NFC_to_FC([1, 1]))  # (600,500)
print(NDC_to_FC([1, 1]))  # (540,440)
print(DC_to_FC([360, 1]))  # (540,440)

DC_to_NDC = lambda x: FC_to_NDC(DC_to_FC(x))

print(DC_to_NDC([0, -1]))  # (0.0, 0.0)
print(DC_to_NDC([180, 0]))  # (0.5, 0.5)
print(DC_to_NDC([360, 1]))  # (1.0, 1.0)