首尾相接数组求子数组最大和

一、题目及要求：

      返回一个整数数组中最大子数组的和

      如果数组A[0]...A[j-1]首尾相邻，允许A[i-1]...A[n-1],A[0]...A[j-1]之和最大；同时返回最大子数组的位置。

二、设计思路：

      对于这题本想延用一维数组的方法，不过由于数组进行了整合，始末位置无法判断。所以此种方法断然没有实现。

小伙伴曾说延用课上学生提供的方法，形成一个固定长度的窗口，依次相加比较。这不失为一个好方法。只可惜时间复杂度不是n。

     于是上网查了点资料。思想有点引用网上的了。首先将为两种情况，一种是跨越a[n-1]，a[0]的。一种是没有跨越的。

      对于没有跨越的，方法很多。对于跨零点的，则可以转换成求其子数组最小和。由于数组总和确定。对于中间那段必定为最小和。总和减最小和求出最大和。对于两个最大和进行比较。得到最终结果。

三、代码

/*王童博  燕亚峰*/
#include<iostream.h>
#include<stdlib.h>
struct ret
{
    int max,start,end;       //用于存放最大值，及始末位置
};

struct ret max2(int arry[],int length)  //跨越arry[n-1]、arry[0]的最大和
{
    int total=0;
    int start1=0;
    int start2;    //起始位置
    int end=0;
    int sum=arry[0];
    int minsum=arry[0];
    for(int i=1;i<length;i++)
    {
        if(sum>0)
        {
            sum=arry[i];
            start1=i;
        }
        else
        {
            sum=sum+arry[i];

        }
        if(minsum>=sum)
        {
            minsum=sum;
            end=i;
            start2=start1;
        }
        total=total+arry[i];
    }
    total=total+arry[0];
    minsum=total-minsum;
    struct ret ret1={minsum,start2,end};
    return ret1;
}


struct ret max1(int arry[],int length)   //不跨越零点的最大和
{
    int start1=0;
    int start2;     //起始位置
    int end=0;
    int sum=arry[0];
    int maxsum=arry[0];
    for(int i=1;i<length;i++)    //求出相邻数组最小和
    {
        if(sum<0)
        {
            sum=arry[i];
            start1=i;
        }
        else
        {
            sum=sum+arry[i];

        }
        if(maxsum<=sum)
        {
            start2=start1;
            end=i;
            maxsum=sum;
        }
    }
    struct ret ret1={maxsum,start2,end};
    return ret1;
}

int main()
{
    srand((unsigned)time(0));
    int N;
    cout<<"输入元素个数:";
    cin>>N;
    int a[20];
    for(int i=0;i<N;i++)
    {
        a[i]=rand()%20-10;
        cout<<a[i]<<"  ";
    }
    cout<<endl;
    struct ret w=max2(a,N);   //调用max2函数，求跨越零点的最值
    struct ret q=max1(a,N);
    if(w.max>q.max)
    {
        cout<<"最大和为:"<<w.max<<"起始位置:"<<w.end+1<<"结束位置:"<<w.start-1;
    }
    else
    {
        cout<<"最大和为:"<<q.max<<"起始位置:"<<q.start<<"结束位置:"<<q.end;
    }
    return 0;
}

四、截图

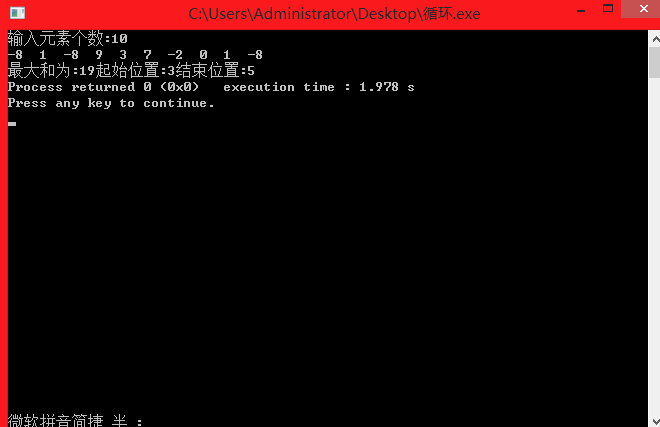
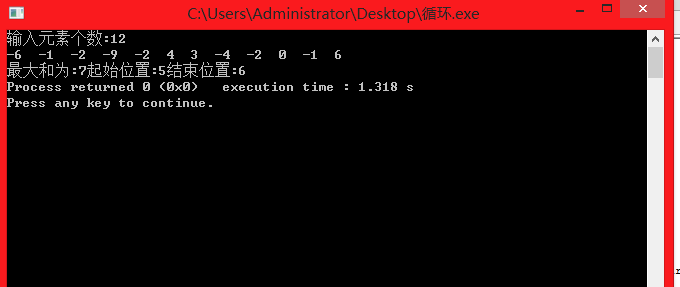
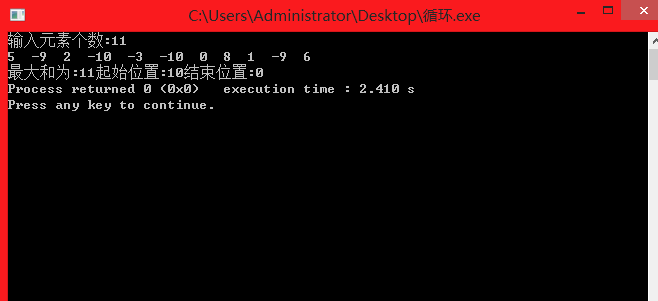
五、实验总结

 对于本次实验还是颇有感悟的，对于有些东西不能过于复杂化。像上次一维数组就可以很简单的解决。但自己却化蛇添足。多了几处不需要的代码。不过也是对自己思想的一种实现。

  这次实验有点借用网上的了。从反方向入手，不失为一种很好的方法，让我想起TED中的一段演讲，凡事都要考虑反面，美国人在日本问街道的名称，得到的回答却是某某街区和某某街区。因为街道是没有命名的。

  对于思路已在思路方面详细阐述了。在这里仅说反向考虑这种思想。

  无论什么方面的事情，似乎都需要双方向考虑。

  最后不得不附上努力思考的疲劳状：