信号的频谱分析,加噪降噪处理
一、题目:
说一段话并录音:信号与系统真有趣,我爱信号与系统,我爱学习。
(1)用Matlab读取语音信号,理解信号含义及抽样频率的含义,并绘制语音信号时域波形。
(2) 语音信号频谱分析,使用FFT分析信号频谱,观察语音信号的频域特性。
(3) 语音信号变换:快放,慢放,叠加噪声等。
(4) 根据频谱分析结果设计带通滤波器,对语音信号进行降噪过滤
二、分析:
1.通过audioread函数来读取信号,通过采样,得到了输入信号的时域信号。然后通过快速傅里叶变换FFT,得到了输入信号的频域(本课程未要求)波形。
2.加入高频和低频信号来模拟噪声。加入到原始的信号中,进而分析混合音频的频谱和时域波形。
3.Sound函数通过改变采样率来实现快放和慢放。
4.首先通过matlab产生的频谱对音频进行频率分析,忽略高频(电流噪声),得到本人的声音频率区间:大部分落在120-200HZ范围内。

为了尽可能的滤掉噪音,不可避免地损失部分原声频率。设计带通滤波器,使它允许通过150-160HZ的滤波器。发现此时的滤波效果最好,同时损失程度不是很大。
5.因为一阶滤波器的滤波效果是有限的,所以最优滤波效果仍然无法满足足够的滤波效果,考虑建立二阶带通滤波器。进行实验。
经查阅资料[1]:二阶带通滤波器与中心角频率和阻尼系数有关:当二阶滤波器的阻尼系数K为0.707时,效果最好。中心角频率ω=2πf,根据实际情况选定f=160HZ。同时二阶带通滤波器的系统函数为: H(s)=Kωs/(s2+Kωs+ω2 )
进行降噪,发现效果优于一阶带通滤波器。
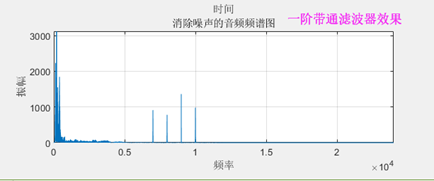
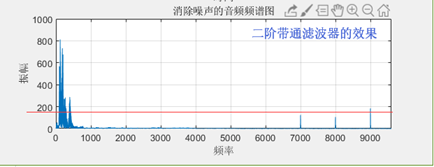
尽管损失了部分原来声音频率,但是很好的滤掉了高频噪声。
三、MATLAB代码如下:
特别注意:录入的音频已经提前通过Au变成单声道文件。
clear;
[y,fs]=audioread('C:UsersDELLDesktop123.wav');
%sound(y,fs);%播放语言信号
%sound(y,0.5*fs);%慢放语言信号
%sound(y,2.5.*fs);%快放语言信号
N=length(y); %信号的长度
T = 1/fs;%采样间隔
t=(0:N-1)/fs;%时域范围
figure(1);
subplot(2,1,1);
plot(t,y); %音频信号时域图
title('音频时域图');
xlabel('Time');ylabel('Amplitude');
Y=fft(y,N);%快速傅里叶变换
subplot(2,1,2);
df=fs/length(Y); %计算谱线间隔
f=0:df:(fs/2-df); %频谱范围,截取前半段(抽样频率高于最大频率的2倍)
Yf=abs(Y); %幅度响应
Yf=Yf(1:length(Yf)/2); %由于幅度响应是偶函数,所以截取一半
plot(f,Yf); %音频信号频谱图
axis([0,fs/5,0,2000]);
title('音频频谱图');
%加入噪声
tt =(1:N);
yn=0.3*cos(25*2*pi/fs*tt')+0.3*cos(20000*2*pi/fs*tt')+0.2*cos(19000*2*pi/fs*tt')+0.2*cos(18000*2*pi/fs*tt')+0.2*cos(17000*2*pi/fs*tt');%加噪声
s=5.*y+yn; %将噪音和原来的音频混合,将原来的声音幅值增大,使得效果更明显
sound(s,fs);%播放带噪音的语言信号
figure(2);
subplot(211);
plot(t,s); %加入噪声的音频时域图
title('加入噪声的音频时域图');
xlabel('时间');ylabel('振幅');
grid;%加入网格
subplot(212);
S=fft(s,N);
Sf=abs(S); %幅度
DF=fs/length(S);%计算谱线间隔
f=0:DF:(fs/2-DF);%频谱范围,截取前半段(抽样频率高于最大频率的2倍)
Sf=Sf(1:length(Sf)/2); %由于幅度响应是偶函数,所以截取一半
axis([0,fs/5,0,10000]);%限制坐标范围能更清楚观察到频谱
plot(f,Sf);
title('加入噪声的音频频谱图');
xlabel('频率');ylabel('振幅');
grid;
%一般男声平均150-160hz
r1=10.61;%电阻阻值(ome)
c1=1*10^(-4);%电容(f)
r2=9.947;%电阻阻值(ome)
c2=1*10^(-4);%电容(f)
Func=tf([1 0],[r1*c1 (1+(r1*c1)/(r2*c2)) 1/(r2*c2)]);%系统的传递函数
%---------------------补充二阶滤波---------------------------------
% omega=2*pi*f,而f是160hz,中心角频率
%二阶滤波器的阻尼系数0.707
k=0.707;
omega=180;
%Func=tf([k.*omega 0],[1 k.*omega omega.*omega]);%二阶系统的传递函数
[yout,tout] = lsim(Func,s,t);%滤波后信号图像
%sound(yout,fs);%
figure(3);
subplot(211);
plot(tout,yout); %消除噪声的音频时域图
title('消除噪声的音频时域图');
xlabel('时间');ylabel('振幅');
grid;
subplot(212);
S=fft(yout,N);
Sf=abs(S); %幅度
DF=fs/length(S);%计算谱线间隔
f=0:DF:(fs/2-DF);%频谱范围,截取前半段(抽样频率高于最大频率的2倍)
Sf=Sf(1:length(Sf)/2); %由于幅度响应是偶函数,所以截取一半
axis([0,fs/5,0,10000]);%限制坐标范围能更清楚观察到频谱
plot(f,Sf);
axis([0,fs/5,0,1000]);
title('消除噪声的音频频谱图');
xlabel('频率');ylabel('振幅');
grid;
四、设计的优缺点
1、本课程设计前期采用的为一阶滤波器,滤波的能力和精确度都很有限,使用二阶滤波的效果提高了精度,仍然很难完全将噪声过滤。
2.本实验通过对滤波器的检验,观察当噪音频率很高或者很低时,低通滤波器和高通滤波器模型的准确度和可行性。。
3.为保证降噪的质量,通过matlab的频谱分析,忽略掉录音时产上的高频电流,得到人声所在频率区间,从而设计合理的带通滤波器。同时针对不同用户选取不同的带通滤波器,达到了个性化和合理化。
五、总结
由于时间所限,本文未能完全发掘信号处理的更多内容。例如信号的快放慢放方面如何保证在快放慢放方面声音的不失真性。以及利用更高阶滤波器更好的实现滤波。后续可以从如何提高滤波精度的方面进行更深的研究。
参考文献:
[1]尉云峰. RC有源滤波器优化综合技术研究[J]. 机电工程,2002,(04):34-35.
[2] 郑君里等. 信号与系统[M]. 北京:高等教育出版社,2011:226-235.