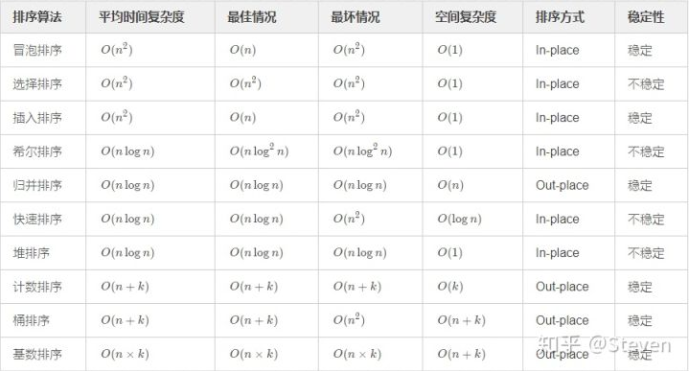
常用的排序算法:
public class Test : MonoBehaviour {
void Swap(int[] arr, int i, int j)
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
/// <summary>
/// 冒泡排序,遍历所有的数据,每次对相邻元素进行两两比较,如果顺序和预先规定的顺序不一致,则进行位置交换;
/// 这样一次遍历会将最大或最小的数据上浮到顶端,之后再重复同样的操作,直到所有的数据有序。
/// 有序序列[len - i,len],未排序序列[0,i]
/// </summary>
/// <param name="arr"></param>
/// <param name="len"></param>
void BubbleSort(int[] arr, int len)
{
for (int i = 0; i < len; i++)
{
for (int j = 0; j < len - 1 - i; j++)
{
if (arr[j] > arr[j + 1])
{
Swap(arr, j, j + 1);
}
}
}
}
/// <summary>
/// 选择排序,每次从未排序的数据中寻找最大或最小的元素,依次放到排序序列中,直到所有数据样本排序完成
/// 有序序列[0,i-1],未排序序列[i,len]
/// </summary>
/// <param name="arr"></param>
/// <param name="len"></param>
void SelectSort(int[] arr, int len)
{
for (int i = 0; i < len; i++)
{
int min = i;
for (int j = i + 1; j < len; j++)
{
if (arr[min] < arr[j])
{
min = j;
}
}
Swap(arr, i, min);
}
}
/// <summary>
/// 插入排序,先将待排序序列的第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列;
/// 然后从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置,直到所有数据都完成排序;
/// 如果待插入的元素与有序序列中的某个元素相等,则将待插入元素插入到相等元素的后面。
/// 有序序列[0,i-1],未排序序列[i,len]
/// </summary>
/// <param name="arr"></param>
/// <param name="len"></param>
void InsertSort(int[] arr, int len)
{
for (int i = 1; i < len; i++)
{
for (int j = i - 1; j > 0; j--)
{
if (arr[i] < arr[j])
{
Swap(arr, i, j);
}
else
break;
}
}
}
/// <summary>
/// 希尔排序,插入排序的一种改进版本,先将整个数据序列分割成若干子序列分别进行直接插入排序,(grap)
/// 待整个序列中的记录基本有序时,再对全部数据进行依次直接插入排序。
/// 有序序列[i,i+grap, i+grap+grap,....],未排序序列[0,grap]
/// </summary>
/// <param name="arr"></param>
/// <param name="len"></param>
void ShellSort(int[] arr, int len)
{
int grap = len / 2;
while (grap > 0)
{
for (int i = grap; i < len; i++)
{
for (int j = i - grap; j >= 0; j -= grap)
{
if (arr[j] < arr[j - grap])
{
Swap(arr, j, j - grap);
}
}
}
grap /= 2;
}
}
/// <summary>
/// 快速排序,首先从数列中挑出一个元素,并将这个元素称为「基准。
/// 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任何一边)。
/// 在这个分区结束之后,该基准就处于数列的中间位置。
/// 之后,在子序列中继续重复这个方法,直到最后整个数据序列排序完成。
/// </summary>
/// <param name="arr"></param>
/// <param name="len"></param>
void QuickSort(int[] arr, int left, int right)
{
if (left >= right) return;
int bound = arr[right];
int end = right;
int start = left;
right -= 1;
while (left < right)
{
while (arr[left] > bound && left < right)
{
left += 1;
}
while (arr[right] < bound && left < right)
{
right -= 1;
}
Swap(arr, left, right);
}
if (arr[left] > bound)
{
Swap(arr, left, end);
}
else {
left++;
}
QuickSort(arr, start, left - 1);
QuickSort(arr, right + 1, end);
}
/// <summary>
/// 归并排序,先将数据样本拆分为n个子数据样本(长度为1), 并分别对它们排序, 最后再将n个子数据样本合并在一起;
///
/// </summary>
/// <param name="arr"></param
/// <param name="temp"></param>长度为len的空数组
/// <param name="len"></param>
void MergeSort(int[] arr, int[] temp, int start, int end)
{
if (start >= end) { return; }
int len = end - start;
int mid = len / 2;
MergeSort(arr, temp, start, mid);
MergeSort(arr, temp, mid, end);
int start1 = start;
int k = start;
int end1 = mid + 1;
while (start1 <= mid && end1 <= end)
{
if (arr[start1] < arr[end1])
{
temp[k++] = arr[end1];
end1++;
}
else
{
temp[k++] = arr[start1];
start1++;
}
}
while (start1 <= mid)
{
temp[k++] = arr[start1];
}
while (end1 <= end)
{
temp[k++] = arr[end1];
}
for (k = start; k <= end; k++)
{
arr[k] = temp[k];
}
}
/// <summary>
/// 计数排序,使用一个额外的数组temp,其中temp[i]是待排序数组arr中值等于i的元素的个数。然后根据数组其中temp来将arr中的元素排到正确的位置。
/// 数组第i个数据arr[i]因该放在temp[arr[i]]位置上
/// 找出待排序的数组中最大和最小的元素
///统计数组中每个值为i的元素出现的次数,存入数组temp的第i项
///对所有的计数累加, 从temp中的第一个元素开始,每一项和前一项相加
///反向填充目标数组, 将每个元素i放在新数组的第temp[i]项,每放一个元素就将temp[i] 减去1
/// </summary>
/// <param name="arr"></param>
/// <param name="len"></param>
/// <param name="max"></param>
void CountSort(int[] arr, int len, int max)
{
int[] temp = new int[max];
for (int i = 0; i < max; i++)
{
temp[i] = 0;
}
for (int i = 0; i < len; i++)
{
temp[arr[i]] += 1;
}
for (int i = 1; i < max; i++)
{
temp[i] += temp[i - 1];
}
int[] sort = new int[len];
for (int i = 0; i < len; i++)
{
temp[arr[i]] -= 1;//数组0开始,所以先减
sort[temp[arr[i]]] = arr[i];//数组第i个数据arr[i]因该放在temp[arr[i]]位置上
}
for (int i = 0; i < len; i++)
{
arr[i] = sort[i];
}
}
/// <summary>
/// 基数排序,整数排序算法,其原理是将整数按位数切割成不同的数字,然后按每个位数分别比较。
/// 从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
/// 例如先排序个位,在排序十位,一次类推。位数排序使用的是计数排序,即位数d的循环嵌套了一层计数排序
/// </summary>
/// <param name="arr"></param>
/// <param name="len"></param>
void RadixSort(int[] arr, int len)
{
int maxBit = GetMaxBit(arr, len);
int[] temp = new int[len];
int[] numCount = new int[10];
int curBit = 1;
for (int i = 0; i < maxBit; i++)
{
for (int j = 0; j < 10; j++)
{
numCount[j] = 0;
}
for (int k = 0; k < len; k++)
{
int num = (arr[k] / curBit) % 10;
numCount[num] += 1;
}
for (int k = 1; k < 10; k++)
{
numCount[k] += numCount[k - 1];
}
for (int k = 0; k < len; k++)
{
int num = (arr[k] / curBit) % 10;
numCount[num] -= 1;
temp[numCount[num]] = arr[k];
}
for (int j = 0; j < len; j++)
{
arr[j] = temp[j];
}
}
}
int GetMaxBit(int[] arr, int len)
{
int max = arr[0];
for (int i = 1; i < len; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
}
int d = 0;
while (max > 0)
{
d += 1;
max /= 10;
}
return d;
}
}