软件工程第三次作业

题目：最大连续子数组和（最大子段和）。

一、问题描述：

给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

二、实现方法：

算法：
使用动态规划法，在对于上述分治算法的分析中我们注意到，若记b[j]=max(a[i]+a[i+1]+..+a[j]),其中1<=i<=j,并且1<=j<=n。则所求的最大子段和为max b[j]，1<=j<=n。
由b[j]的定义可易知，当b[j-1]>0时b[j]=b[j-1]+a[j]，否则b[j]=a[j]。故b[j]的动态规划递归式为:b[j]=max(b[j-1]+a[j],a[j])，1<=j<=n。
算法实现的代码： 类的定义、算法的实现、算法的测试
代码：

// ConsoleApplication2.cpp: 定义控制台应用程序的入口点。
//
#include "stdafx.h"
#include <stdlib.h>
#include<stdio.h>
#include <iostream>
using namespace std;
int main()
{
	int count;
	int a[100];
	int b[100];
	int i;
	int max;
	cin >> count;
	for (i = 0; i<count; i++)
	{
		cin >> a[i];
	}
	b[0] = a[0];
	max = b[0];
	for (i = 1; i<count; i++)
	{
		if (b[i - 1]>0)
			b[i] = b[i - 1] + a[i];
		else
			b[i] = a[i];
		if (b[i]>max)
			max = b[i];
	}
	printf("%d
", max);
	return 0;
}

三、运行及样例测试

在解决方案中添加单元测试

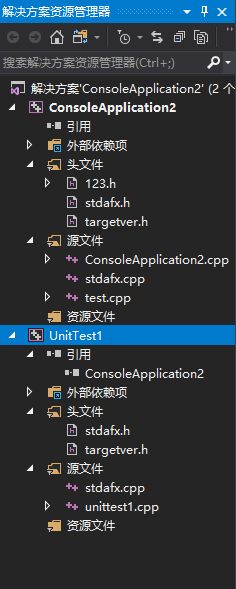
代码运行成功后进行样例测试，选取语句覆盖的覆盖标准，通过多组测试样例覆盖所有程序语句实现对程序的测试

测试单元的属性修改

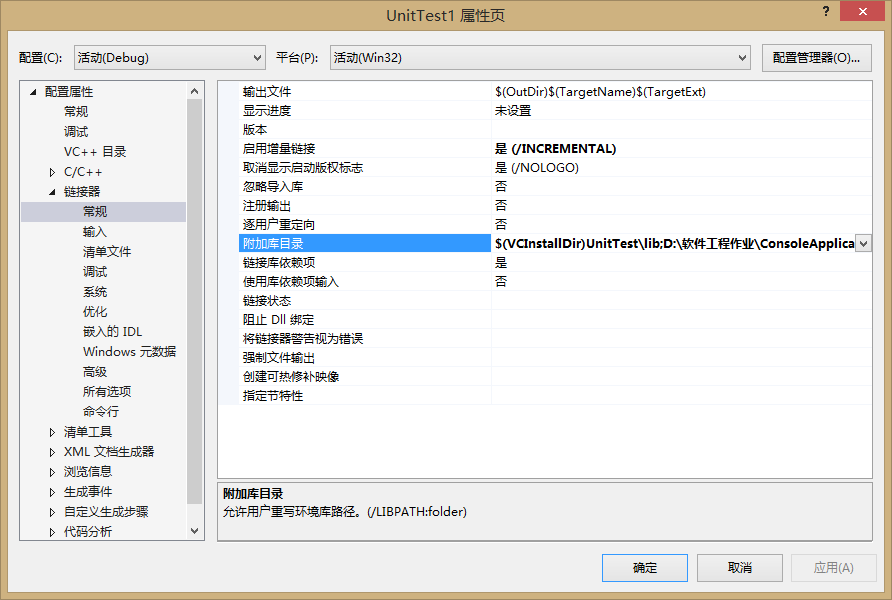
测试资源

#include "stdafx.h"
#include "CppUnitTest.h"
#include "..ConsoleApplication2123.h"

using namespace Microsoft::VisualStudio::CppUnitTestFramework;

namespace UnitTest1
{		
	TEST_CLASS(UnitTest1)
	{
	public:
		
		TEST_METHOD(TestMethod1)
		{
			// TODO: 在此输入测试代码
			int count = 0;
			int a[100] = { };
			point t = point(a, count);
			Assert::AreEqual(0, t.GetMax());
		}
		TEST_METHOD(TestMethod2)
		{
			// TODO: 在此输入测试代码
			int count = 6;
			int a[100] = { -2,11,-4,13,-5,-2 };
			point t = point(a, count);
			Assert::AreEqual(20, t.GetMax());
		}
		TEST_METHOD(TestMethod3)
		{
			// TODO: 在此输入测试代码
			int count = 5;
			int a[100] = {-1,-2,-3,-4,-5};
			point t = point(a, count);
			Assert::AreEqual(0, t.GetMax());
		}
		TEST_METHOD(TestMethod4)
		{
			// TODO: 在此输入测试代码
			int count = 5;
			int a[100] = {-4,6,9,-11,12};
			point t = point(a, count);
			Assert::AreEqual(16, t.GetMax());
		}

	};
}

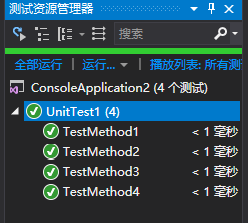
测试结果：

附录：

代码连接 最大子数组和