1. 问题 某市有甲、乙、丙、丁四个居民区,自来水有A,B,C三个水库供应。四个区每天必须得到保证的基本用水量分别是30,70,10,10千吨,但由于水源紧张,三个水库每天最多只能分别供应50,60,50千吨自来水。由于地理位置的差别,自来水公司从各水库向各区送水所需付出的引水管理费不同(见表1,其中C水库与丁区之间没有输水管道),其他管理费用都是450元/千吨。根据公司规定,各区用户按照统一标准900元/千吨收费。此外,四个区都向公司申请了额外用水量,分别为50,70,20,40千吨。该公司应如何分配供水量,才能获利最多?
为了增加供水量,自来水公司正在考虑进行水库改造,使三个水库每天的最大供水量都提高一倍,问那时供水方案应如何改变?公司利润可增加到多少?
表1 从水库向各区送水的引水管理费
|
引水管理费(元/吨) |
甲 |
乙 |
丙 |
丁 |
|
A |
160 |
130 |
220 |
170 |
|
B |
140 |
130 |
190 |
150 |
|
C |
190 |
200 |
230 |
/ |
model:
sets:
water/1,2,3/:sup;
house/1,2,3,4/:use;
links(water,house):c,x;
endsets
data:
c=160 130 220 170
140 130 190 150
190 200 230 0;
enddata
min=@sum(links(I,J):c(I,J)*x(I,J));
x(3,1)+x(3,2)+x(3,3)=50;
x(1,1)+x(1,2)+x(1,3)+x(1,4)=50;
x(2,1)+x(2,2)+x(2,3)+x(2,4)=60;
x(1,4)+x(2,4)>=10;
x(1,4)+x(2,4)<=50;
x(1,1)+x(2,1)+x(3,1)>=30;
x(1,1)+x(2,1)+x(3,1)<=80;
x(1,2)+x(2,2)+x(3,2)>=70;
x(1,2)+x(2,2)+x(3,2)<=140;
x(1,3)+x(2,3)+x(3,3)>=10;
x(1,3)+x(2,3)+x(3,3)<=30;
end
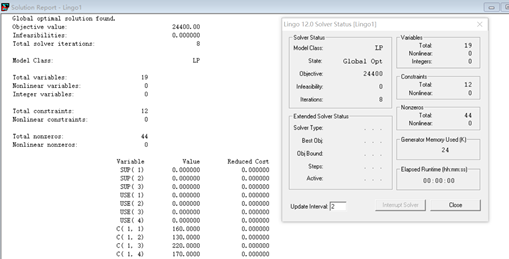
从水库向各区送水方案
|
送水量 (千吨) |
甲 |
乙 |
丙 |
丁 |
|
A |
0 |
50 |
0 |
0 |
|
B |
0 |
50 |
0 |
10 |
|
C |
40 |
0 |
10 |
/ |
引水管理费为24400元,利润为(900-450)*(50+60+50)-24400=47600元
对于问题二,总供水能力为320,大于总需求300,水库供水量不能全部卖出,因而计算净利润=900-450-引水管理费,得下表
从水库向各区送水净利润
|
送水量 (千吨) |
甲 |
乙 |
丙 |
丁 |
|
A |
290 |
320 |
230 |
280 |
|
B |
310 |
320 |
260 |
300 |
|
C |
260 |
250 |
220 |
/ |
model:
sets:
water/1,2,3/:sup;
house/1,2,3,4/:use;
links(water,house):c,x;
endsets
data:
c=290 320 230 280
310 320 260 300
260 250 220 0;
enddata
max=@sum(links(I,J):c(I,J)*x(I,J));
x(3,1)+x(3,2)+x(3,3)<=100;
x(1,1)+x(1,2)+x(1,3)+x(1,4)<=100;
x(2,1)+x(2,2)+x(2,3)+x(2,4)<=120;
x(1,4)+x(2,4)>=10;
x(1,4)+x(2,4)<=50;
x(1,1)+x(2,1)+x(3,1)>=30;
x(1,1)+x(2,1)+x(3,1)<=80;
x(1,2)+x(2,2)+x(3,2)>=70;
x(1,2)+x(2,2)+x(3,2)<=140;
x(1,3)+x(2,3)+x(3,3)>=10;
x(1,3)+x(2,3)+x(3,3)<=30;
end
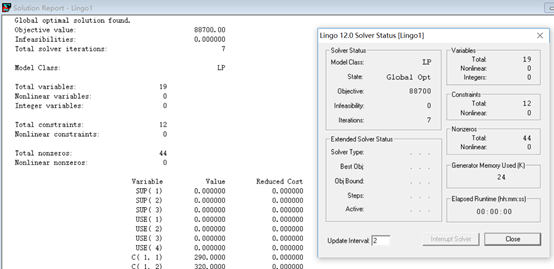
总利润为88700元。
2.问题 某公司用两种原油A、B混合加工成两种汽油甲、乙。甲、乙两种汽油含原油A的最低比例分别为50%和60%,每吨售价分别为4800元和5600元。该公司现有原油A和B的库存量分别为 500吨和1000吨,还可以从市场上买到不超过1500吨的原油A。原油A的市场价为:购买量不超过500吨时的单价为10000元/吨;购买量超过500吨但不超过1000吨时,超过500吨部分的单价为8000元/吨;购买量超过1000吨时,超过1000吨部分的单价为6000元/吨。该公司应如何安排原有的采购和加工?
问题分析 本题主要通过安排原油的采购量及加工量,以获得最大利润,故决策变量为原油A的采购量以及两种原油的加工量,目标函数为甲乙两种汽油的利润之和,限制条件为甲乙两种汽油的原油A的含量,原油A的库存量及采购量,原油B的库存量。
model:
sets:
oil/1,2/:y;
qiyou/1,2/:q;
sale/1,2,3/:m;
pro/1,2,3/:pr;
link(oil,qiyou):c,x;
endsets
data:
c=4.8,5.6,4.8,5.6;
y=500,1000;
pr=10,8,6;
enddata
max=@sum(link:c*x)-@sum(sale:m*pr);
ml=@sum(sale:m);
ml<1500;
@sum(qiyou(j):x(1,j))<y(1)+ml;
@sum(qiyou(j):x(2,j))<y(2);
x(1,1)-x(2,1)>0;
2*x(1,2)-3*x(2,2)>0;
(m(1)-500)*m(2)=0;
(m(2)-500)*m(3)=0;
@for(sale(i):m(i)<500;);
end

利润为4800千元。