• 矩阵小结

    前沿：之前之做过一些递推关系式简单的矩阵快速幂，看了大牛的博客发现对于那种方程两边有多个不同的未知变量也可以用矩阵解决：http://blog.csdn.net/abcjennifer/article/details/5302198，于是找了几道题练手，顺便分享一下经验。

    题目链接：http://acm.fzu.edu.cn/problem.php?pid=1683

    思路：直接给出递推关系式：S(n)=S(n-1)+F(n)=S(n-1)+3*F(n-1)+2*F(n-2)+7*F(n-3).于是写成矩阵的形式：

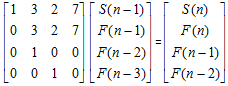
    从而求的S(n).

     1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 const int MOD=2009;
 7 
 8 int n;
 9 struct Matrix{
10     int map[4][4];
11 }Mata,Matb;
12 
13 void Initiate()
14 {
15     for(int i=0;i<4;i++)
16         for(int j=0;j<4;j++)
17             Mata.map[i][j]=0;
18     Mata.map[0][0]=1,Mata.map[0][1]=3;
19     Mata.map[0][2]=2,Mata.map[0][3]=7;
20 
21     Mata.map[1][1]=3,Mata.map[1][2]=2;
22     Mata.map[1][3]=7;
23 
24     Mata.map[2][1]=Mata.map[3][2]=1;
25 }
26 
27 
28 Matrix Mul(const Matrix &a,const Matrix &b)
29 {
30     Matrix c;
31     for(int i=0;i<4;i++){
32         for(int j=0;j<4;j++){
33             c.map[i][j]=0;
34             for(int k=0;k<4;k++){
35                 c.map[i][j]+=a.map[i][k]*b.map[k][j];
36                 c.map[i][j]%=MOD;
37             }
38         }
39     }
40     return c;
41 }
42 
43 Matrix Pow(Matrix &q,int n)
44 {
45     Matrix p;
46     for(int i=0;i<4;i++)
47         for(int j=0;j<4;j++)
48             p.map[i][j]=(i==j)?1:0;
49     while(n){
50         if(n&1){
51             p=Mul(p,q);
52         }
53         n>>=1;
54         q=Mul(q,q);
55     }
56     return p;
57 }
58 
59 int main()
60 {
61     int _case,t=1;
62     scanf("%d",&_case);
63     while(_case--){
64         scanf("%d",&n);
65         printf("Case %d: ",t++);
66         if(n==0)puts("1");
67         else if(n==1)puts("4");
68         else if(n==2)puts("9");
69         else {
70             Initiate();
71             Matb=Pow(Mata,n-2);
72             printf("%d
",(Matb.map[0][0]*9+Matb.map[0][1]*5+Matb.map[0][2]*3+Matb.map[0][3]*1)%MOD);
73         }
74     }
75     return 0;
76 }
    View Code

    题目链接：http://acm.fzu.edu.cn/problem.php?pid=2117

    思路：设a(n)表示n位数且7、9的出现的个数均为偶数的组数，b(n)表示7出现偶数次，9出现奇数次的组数，c(n)表示7出现奇数次，9出现偶数次的组数，d(n)表示7、9均出现奇数次的组数，于是有下列递推关系式：

    a(n)=3*a(n-1)+b(n-1)+c(n-1);

    b(n)=a(n-1)+3*b(n-1)+d(n-1);

    c(n)=a(n-1)+3*c(n-1)+d(n-1);

    d(n)=b(n-1)+c(n-1)+3*d(n-1);

    于是可以构造矩阵：

    [3，1，1，0]    [a(n-1)]       [a(n)]

    [1，3，0，1]    [b(n-1)]   =  [b(n]

    [1，0，3，1]    [c(n-1)]       [c(n)]

    [0，1，1，3]    [d(n-1)]       d[(n)]

    从而矩阵快速幂求a(n)即可。

     1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 const int MOD=1000000007;
 7 
 8 long long n;
 9 struct Matrix{
10     long long map[4][4];
11 }Mata,Matb;
12 
13 
14 void Initiate()
15 {
16     Mata.map[0][0]=3,Mata.map[0][1]=1;
17     Mata.map[0][2]=1,Mata.map[0][3]=0;
18 
19     Mata.map[1][0]=1,Mata.map[1][1]=3;
20     Mata.map[1][2]=0,Mata.map[1][3]=1;
21 
22     Mata.map[2][0]=1,Mata.map[2][1]=0;
23     Mata.map[2][2]=3,Mata.map[2][3]=1;
24 
25     Mata.map[3][0]=0,Mata.map[3][1]=1;
26     Mata.map[3][2]=1,Mata.map[3][3]=3;
27 }
28 
29 Matrix Mul(const Matrix &a,const Matrix &b)
30 {
31     Matrix c;
32     for(int i=0;i<4;i++){
33         for(int j=0;j<4;j++){
34             c.map[i][j]=0;
35             for(int k=0;k<4;k++){
36                 c.map[i][j]+=a.map[i][k]*b.map[k][j];
37                 c.map[i][j]%=MOD;
38             }
39         }
40     }
41     return c;
42 }
43 
44 Matrix Pow(Matrix q,long long  n)
45 {
46     Matrix p;
47     for(int i=0;i<4;i++)
48         for(int j=0;j<4;j++)
49             p.map[i][j]=(i==j)?1:0;
50     while(n){
51         if(n&1){
52             p=Mul(p,q);
53         }
54         n>>=1;
55         q=Mul(q,q);
56     }
57     return p;
58 }
59 
60 
61 int main()
62 {
63     Initiate();
64     int _case;
65     scanf("%d",&_case);
66     while(_case--){
67         scanf("%I64d",&n);
68         if(n==1)puts("3");
69         else {
70             Matb=Pow(Mata,n-1);
71         //    cout<<Matb.map[0][0]<<"**"<<Matb.map[0][1]<<"**"<<Matb.map[0][2]<<endl;
72             long long ans=(Matb.map[0][0]*3+Matb.map[0][1]*1+Matb.map[0][2]*1)%MOD;
73             printf("%I64d
",ans);
74         }
75     }
76     return 0;
77 }
    View Code

    题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3306

    思路：这道题与前几道有所不同，辅助矩阵不定，不过也好办。

    这里直接给出递推式：S(n)=S(n-1)+A(n)^2=S(n-1)+x^2*A(n-1)^2+y^2*A(n-2)^2+2*x*y*A(n-1)*A(n-2);

    于是构造矩阵：

    | S(n)           |      | 1  X^2  Y^2  2XY |     | S(n-1)           |
    | A(n)^2       | =   | 0  x^2  Y^2  2XY |     | A(n-1)^2       |
    | A(n-1)^2    |      | 0  1      0      0     |     | A(n-2)^2       |
    | A(n)A(n-1) |       | 0   X     0      Y    |      | A(n-1)A(n-2) |

    于是就可以用矩阵快速幂求解S(n)了。

     1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 #define MOD 10007
 7 
 8 struct Matrix{
 9     int map[4][4];
10 }Mata,Matb;
11 
12 void Initiate(int x,int y)
13 {
14     for(int i=0;i<4;i++)
15         for(int j=0;j<4;j++)
16             Mata.map[i][j]=0;
17     Mata.map[0][0]=1,Mata.map[0][1]=(x*x)%MOD;
18     Mata.map[0][2]=(y*y)%MOD,Mata.map[0][3]=(2*x*y)%MOD;
19 
20     Mata.map[1][1]=(x*x)%MOD;Mata.map[1][2]=(y*y)%MOD;
21     Mata.map[1][3]=(2*x*y)%MOD;
22 
23     Mata.map[2][1]=1;
24 
25     Mata.map[3][1]=x,Mata.map[3][3]=y;
26 }
27     
28 Matrix Mul(const Matrix &a,const Matrix &b)
29 {
30     Matrix c;
31     for(int i=0;i<4;i++){
32         for(int j=0;j<4;j++){
33             c.map[i][j]=0;
34             for(int k=0;k<4;k++){
35                 c.map[i][j]+=a.map[i][k]*b.map[k][j];
36                 c.map[i][j]%=MOD;
37             }
38         }
39     }
40     return c;
41 }
42 
43 Matrix Pow(Matrix q,int n)
44 {
45     Matrix p;
46     for(int i=0;i<4;i++)
47         for(int j=0;j<4;j++)
48             p.map[i][j]=(i==j)?1:0;
49     while(n){
50         if(n&1){
51             p=Mul(p,q);
52         }
53         n>>=1;
54         q=Mul(q,q);
55     }
56     return p;
57 }
58 
59 int main()
60 {
61     int n,x,y,sum;
62     while(~scanf("%d%d%d",&n,&x,&y)){
63         x%=MOD,y%=MOD;
64         if(n==2){
65             sum=1+1+((x+y)%MOD*(x+y)%MOD)%MOD;
66             printf("%d
",sum);
67         }else {
68             Initiate(x,y);
69             Matb=Pow(Mata,n-1);
70 //            cout<<Matb.map[0][0]<<"**"<<Matb.map[0][1]<<"**"<<Matb.map[0][2]<<"**"<<Matb.map[0][3]<<endl;
71             sum=(2*Matb.map[0][0]+1*Matb.map[0][1]+1*Matb.map[0][2]+1*Matb.map[0][3])%MOD;
72             printf("%d
",sum);
73         }
74     }
75     return 0;
76 }
    View Code

    题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4686

    思路：与上一题类似,直接给出递推式：S(n)=S(n-1)+F(n-1)*G(n-1)=S(n-1)+ax*bx*F(n-2)*G(n-2)+ax*by*F(n-2)+ay*bx*G(n-2)+ay*by。

    于是构造矩阵：

    [ 1,ax*bx,ax*by,ay*bx,ay*by]     [      S(n-1)         ]        [     S(n)             ]

    [ 0,ax*bx,ax*by,ay*bx,ay*by]     [  F(n-2)*G(n-2) ]        [  F(n-1)*G(n-1) ]

    [ 0,     0,     ax,       0,      ay]     [    F(n-2)           ]  =    [    F(n-1)           ]

    [ 0,     0,      0,       bx,     by]     [   G(n-2)           ]        [    G(n-1)           ]

    [ 0,     0,      0,        0,       1]     [        1               ]        [        1               ]

    从而矩阵快速幂求出S(n);

     1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 #define MOD 1000000007
 7 typedef long long ll;
 8 
 9 struct Matrix{
10     ll map[5][5];
11 }Mata,Matb;
12 
13 void Initiate(ll ax,ll ay,ll bx,ll by)
14 {
15     for(int i=0;i<5;i++)
16         for(int j=0;j<5;j++)
17             Mata.map[i][j]=0;
18     Mata.map[0][0]=1,Mata.map[0][1]=ax*bx%MOD;
19     Mata.map[0][2]=ax*by%MOD,Mata.map[0][3]=ay*bx%MOD;
20     Mata.map[0][4]=ay*by%MOD;
21 
22     Mata.map[1][1]=ax*bx%MOD,Mata.map[1][2]=ax*by%MOD;
23     Mata.map[1][3]=ay*bx%MOD,Mata.map[1][4]=ay*by%MOD;
24 
25     Mata.map[2][2]=ax,Mata.map[2][4]=ay;
26 
27     Mata.map[3][3]=bx,Mata.map[3][4]=by;
28 
29     Mata.map[4][4]=1;
30     /*
31     for(int i=0;i<5;i++){
32         for(int j=0;j<5;j++){
33             cout<<Mata.map[i][j]<<" ";
34         }
35         cout<<endl;
36     }*/
37 }
38 
39 Matrix Mul(const Matrix &a,const Matrix &b)
40 {
41     Matrix c;
42     for(int i=0;i<5;i++){
43         for(int j=0;j<5;j++){
44             c.map[i][j]=0;
45             for(int k=0;k<5;k++){
46                 c.map[i][j]+=a.map[i][k]*b.map[k][j];
47                 c.map[i][j]%=MOD;
48             }
49         }
50     }
51     return c;
52 }
53 
54 Matrix Pow(Matrix q,ll n)
55 {
56     Matrix p;
57     for(int i=0;i<5;i++)
58         for(int j=0;j<5;j++)
59             p.map[i][j]=(i==j)?1:0;
60     while(n){
61         if(n&1){
62             p=Mul(p,q);
63         }
64         n>>=1;
65         q=Mul(q,q);
66     }
67     return p;
68 }
69 
70 
71 int main()
72 {
73    // freopen("1.txt","r",stdin);
74     ll n,a0,ax,ay,b0,bx,by,sum,sum1;
75     while(~scanf("%I64d%I64d%I64d%I64d%I64d%I64d%I64d",&n,&a0,&ax,&ay,&b0,&bx,&by)){
76         if(n==0)puts("0");
77         else if(n==1){
78             sum=(a0*b0)%MOD;
79             printf("%I64d
",sum);
80         }else {
81             Initiate(ax,ay,bx,by);
82             Matb=Pow(Mata,n-1);
83             sum1=(a0*b0)%MOD;
84         //    cout<<Matb.map[0][0]<<"**"<<Matb.map[0][1]<<"***"<<Matb.map[0][2]<<"***"<<Matb.map[0][3]<<"**"<<Matb.map[0][4]<<endl;
85             sum=(sum1*Matb.map[0][0]%MOD+(a0*b0%MOD)*Matb.map[0][1]%MOD+(a0*Matb.map[0][2]%MOD)+(b0*Matb.map[0][3]%MOD)+Matb.map[0][4])%MOD;
86             printf("%I64d
",sum);
87         }
88     }
89     return 0;
90 }
    View Code

    题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2971

    思路：与上一道类似，直接给出递推式：S(n)=S(n-1)+F(n)^2=S(n-1)+4*x*x*F(n-1)^2-4*x*F(n-1)*F(n-2)+F(n-2)^2。

    于是构造矩阵：

    [1,4*x*x,-4*x,1]   [S(n-1)           ]          [S(n)           ]

    [0,4*x*x,-4*x,1]   [F(n-1)^2       ]     =   [F(n)^2        ]

    [0, 2*x,  -1,   0]   [F(n-1)*F(n-2)]          [F(n)*F(n-1)]

    [0,   1,    0,   0]   [F(n-2)^2        ]         [F(n-1)^2     ]

    从而矩阵快速幂求出S(n)。

    PS：这里由于有负数出现，取模的时候得小心。

     1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 typedef long long ll;
 7 
 8 ll n,x,m,sum;
 9 struct Matrix{
10     ll map[4][4];
11 }Mata,Matb;
12 
13 void Initiate(ll x)
14 {
15     for(int i=0;i<4;i++)
16         for(int j=0;j<4;j++)
17             Mata.map[i][j]=0;
18     Mata.map[0][0]=1,Mata.map[0][1]=(4*x*x)%m;
19     Mata.map[0][2]=(m-4*x%m)%m,Mata.map[0][3]=1;
20 
21     Mata.map[1][1]=4*x*x%m,Mata.map[1][2]=(m-4*x%m)%m;//处理负数
22     Mata.map[1][3]=1;
23 
24     Mata.map[2][1]=2*x%m,Mata.map[2][2]=m-1;//处理负数
25 
26     Mata.map[3][1]=1;
27 }
28 
29 Matrix Mul(const Matrix &a,const Matrix &b)
30 {
31     Matrix c;
32     for(int i=0;i<4;i++){
33         for(int j=0;j<4;j++){
34             c.map[i][j]=0;
35             for(int k=0;k<4;k++){
36                 c.map[i][j]+=a.map[i][k]*b.map[k][j];
37                 if(c.map[i][j]>=m)c.map[i][j]%=m;
38             }
39         }
40     }
41     return c;
42 }
43 
44 Matrix Pow(Matrix q,ll n)
45 {
46     Matrix p;
47     for(int i=0;i<4;i++)
48         for(int j=0;j<4;j++)
49             p.map[i][j]=(i==j)?1:0;
50     while(n){
51         if(n&1){
52             p=Mul(p,q);
53         }
54         n>>=1;
55         q=Mul(q,q);
56     }
57     return p;
58 }
59 
60 int main()
61 {
62   //  freopen("1.txt","r",stdin);
63     int _case;
64     scanf("%d",&_case);
65     while(_case--){
66         scanf("%I64d%I64d%I64d",&x,&n,&m);
67         if(n==2){
68             sum=(1*1+x*x)%m;
69             printf("%I64d
",sum);
70         }else {
71             Initiate(x);
72             Matb=Pow(Mata,n-2);
73  //           cout<<Matb.map[0][0]<<"**"<<Matb.map[0][1]<<"**"<<Matb.map[0][2]<<"***"<<Matb.map[0][3]<<endl;
74             sum=((((1+x*x)%m)*Matb.map[0][0])%m+((x*x%m)*Matb.map[0][1]%m)+(x*Matb.map[0][2])%m+Matb.map[0][3])%m;
75             printf("%I64d
",sum);
76         }
77     }
78     return 0;
79 }
    View Code

    题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=3519

    思路：令a(n)代表合法的个数，b(n)代表末两位不同,C(n)代表末两位相同。于是我们有如下递推关系式：

    a(n)=2*a(n-1)+C(n-1);

    b(n)=b(n-1)+C(n-1);

    C(n)=b(n-1);

    从而根据上式得出矩阵：

    [2,0,1]   [a(n-1)]      [a(n)]

    [0,1,1]   [b(n-1)]  =  [b(n)]

    [0,1,0]   [C(n-1)]     [C(n)]

    从而矩阵快速幂求出a(n).

     1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 using namespace std;
 6 #define MOD 10007
 7 
 8 struct Matrix{
 9     int map[3][3];
10 }Mata,Matb;
11 
12 Matrix Mul(const Matrix &a,const Matrix &b)
13 {
14     Matrix c;
15     for(int i=0;i<3;i++){
16         for(int j=0;j<3;j++){
17             c.map[i][j]=0;
18             for(int k=0;k<3;k++){
19                 c.map[i][j]+=(a.map[i][k]*b.map[k][j]);
20                 c.map[i][j]%=MOD;
21             }
22         }
23     }
24     return c;
25 }
26 
27 Matrix Pow(Matrix q,int n)
28 {
29     Matrix p;
30     for(int i=0;i<3;i++)
31         for(int j=0;j<3;j++)
32             p.map[i][j]=(i==j)?1:0;
33     while(n){
34         if(n&1){
35             p=Mul(p,q);
36         }
37         n>>=1;
38         q=Mul(q,q);
39     }
40     return p;
41 }
42 
43 int main()
44 {
45     Mata.map[0][0]=2,Mata.map[0][2]=1;
46     Mata.map[1][1]=Mata.map[1][2]=1;
47     Mata.map[2][1]=1;
48     int n;
49     while(~scanf("%d",&n)){
50         if(n<=2)puts("0");
51         else {
52             Matb=Pow(Mata,n-2);
53             printf("%d
",2*(Matb.map[0][1]+Matb.map[0][2])%MOD);
54         }
55     }
56     return 0;
57 }
    View Code
  • 相关阅读:
    signal(SIGCHLD, SIG_IGN)和signal(SIGPIPE, SIG_IGN);
    关于pthread_cond_wait使用while循环判断的理解
    linux的sleep()和usleep()的使用和区别
    C中结构体的存储分配
    扯扯python的多线程的同步锁 Lock RLock Semaphore Event Condition
    线程属性的初始化以及销毁
    Mysql数据库一个表字段中存了id,并以逗号分隔,id对应的详细信息在另一个表中
    sqlyog 注册码
    Oracle 12C卸载图文教程
    Oracle12c Release1安装图解（详解）
  • 原文地址：https://www.cnblogs.com/wally/p/3271073.html
Copyright © 2020-2023  润新知