LeetCode 514 自由之路
https://leetcode-cn.com/problems/freedom-trail/
动态规划
这是一道困难题,不要被它吓到了,我们一步一步往下分析。首先点开“相关标签”,我们发现力扣站在上帝视角给出了它的提示——动态规划。既然如此,我们就顺着动态规划的思路往下分析。
我们先考虑解决这题需要考虑哪些状态。请问要想将字符拼写过程进行下去,我们需要知道哪些变量?答:两个指针i和j,它们分别指向了字符串key和ring,表示当前我们需要拼写的字符是key[i]并且此时字符ring[j]是与12点种方向对齐的。那么,我们不妨定义dp[i][j]表示在字符ring[j]与12点钟方向对齐的情况下,拼写出字符key[i]所需的最少步数。
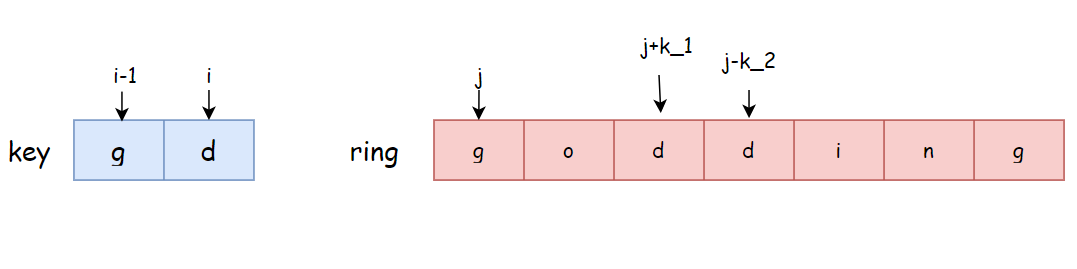
接下来,我们考虑状态转移方程是怎样的。对于字符key[i]和ring[j],它们只存在两种情况,即相等或不相等。当key[i] != ring[j]时,我们能够直接拼写出字符key[i]吗?大家可能会觉得这不废话吗,肯定是不能呀!是的,确实不能,但我们不妨仔细考虑一下这种情况。如下图所示,我们要拼写字符d,但指针j指向的却是字符o。此时,无法直接拼写出字符d。因为要求所需的步数是最少的,所以一个合理的拼写方案是当指针j == 0时拼写出key[i]的前一个字符g,然后指针j往前移动两步,此时j == 2,刚好有ring[j] == key[i],拼写出字符d。换句话说,在拼写字符串key的过程中,当拼写完key[i-1]后准备拼写key[i]的时,指针j压根就不会停留在一个和key[i]不相等的字符上。也即下图这种情况在拼写过程中是不存在的。

如下图所示,当我们拼写完字符key[i-1]之后,准备拼写key[i]时,此时指针指针j要么是往前移动(k_1)步要么是往后移动(k_2)步(对应逆时针和顺时针旋转)找到一个和key[i]相等的且离得最近的字符然后停下。因为要求的是最少的移动步数,所以需要取这两种移动方案中步数最少的,在这个最少的移动步数的基础上加上1次按确认的步数。
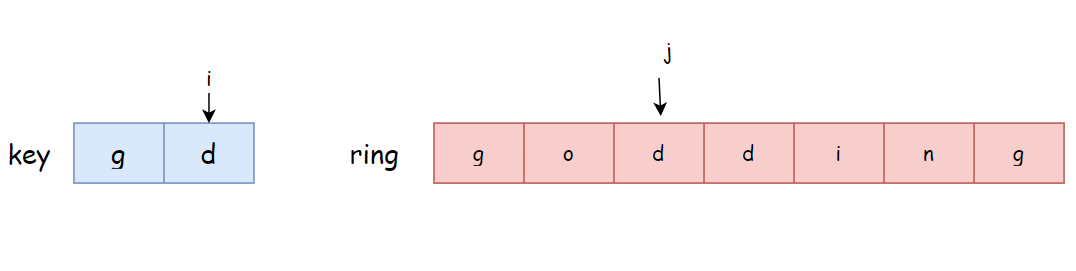
以上是正向思考过程,为了得到当前移动步数和之前移动步数的关系以构建状态转移方程,我们需要逆向思考。如下图所示,假设此时key[i] == ring[j],我们要求dp[i][j]的值。通过上面的分析,我们可以知道上一次移动之后,指针j一定停留在和字符key[i-1]相等的位置处。并且和字符key[i-1]相等的位置可能有多个,假设这些位置保存在集合pos(key[i-1])中。因为下一次指针j的指向可能是由集合pos(key[i-1])中任意一个位置以顺时针或者逆时针的方式移动而来。所以我们终于可以得到状态转移方程如下:
简要解释如下:
- (pos(key[i-1]))指的是字符串
ring中所有和字符key[i-1]相等的字符所处的位置的集合 - (dp[i-1][p])表示拼写字符
key[i-1]所需要的最少步数,求拼写key[i]所需的最小步数需要在它的基础上加上公式后面的计算结果 - (abs(j-p))和(len - abs(j-p))分别表示了顺时针和逆时针情况下从位置
p移动到位置j所需的移动步数。其中的(len)表示字符串ring的长度,后续的加1表示按确认所耗费的一次移动步数
最后,我们考虑边界情况和返回什么作为答案。可以看到要计算dp[i][j],我们需要直到所有的dp[i-1][p]。因而我们需要提前计算的边界就是dp[0][p]。易知,我们应该返回dp[sz2 - 1]这一行中的最小值作为答案。
分析清楚之后,我们可以将上面的过程用如下代码来实现。
class Solution {
public:
int findRotateSteps(string ring, string key) {
int sz1 = ring.size(); // j
int sz2 = key.size(); // i
vector<int> pos[26];
for (int j = 0; j < sz1; ++j)
pos[ring[j] - 'a'].push_back(j);
// 计算边界
vector<vector<int>> dp(sz2, vector<int>(sz1, INT_MAX));
for (int p : pos[key[0] - 'a']) {
// 因为一开始是ring的第一个字符对着12点种方向的,所以对于每一个下标p,
// 逆时针和顺时针旋转到p处需耗费移移次数是p和sz1-p。再加上1次确认步骤
dp[0][p] = min(p, sz1 - p) + 1;
}
// 递推过程
for (int i = 1; i < sz2; ++i) {
for (int j : pos[key[i] - 'a']) { // pos[key[i] - 'a']表示当前这步指针j可以停留的位置
for (int p : pos[key[i - 1] - 'a']) { // pos[key[i - 1] - 'a']表示上一步指针j可以停留的位置
dp[i][j] = min(dp[i][j], dp[i - 1][p] + min(abs(j - p), sz1 - abs(j - p)) + 1);
}
}
}
int ans = INT_MAX;
for (int j = 0; j < sz1; ++j) {
ans = min(ans, dp[sz2 - 1][j]);
}
return ans;
}
};