2020-09-21：已知最大公约数和最小公倍数，如何判断这两个数是否存在？

福哥答案2020-09-21：#福大大架构师每日一题#

1.如果最大公约数或者最小公倍数有小于1的，不存在这两个数。
2.如果最大公约数等于1，存在这两个数。这个步骤可以不要。
3.如果最大公约数大于最小公倍数，不存在这两个数。这个步骤可以不要。
4.如果最小公倍数不能被最大公约数整除，不存在这两个数。
5.通过所有考验，一定存在这种两个数。

代码用go语言编写。代码如下：

package test42_gcd_lcm

import (
    "fmt"
    "testing"
)

//go test -v -test.run TestGcdIsExistTwoNumsByGcdLcm
func TestGcdIsExistTwoNumsByGcdLcm(t *testing.T) {
    gcd := 0
    lcm := 0

    gcd = 3
    lcm = 60
    fmt.Println("gcd =", gcd, ",lcm =", lcm, "。", IsExistTwoNumsByGcdLcm(gcd, lcm))

    gcd = 5
    lcm = 10
    fmt.Println("gcd =", gcd, ",lcm =", lcm, "。", IsExistTwoNumsByGcdLcm(gcd, lcm))

    gcd = 5
    lcm = 50
    fmt.Println("gcd =", gcd, ",lcm =", lcm, "。", IsExistTwoNumsByGcdLcm(gcd, lcm))

    gcd = 5
    lcm = 20
    fmt.Println("gcd =", gcd, ",lcm =", lcm, "。", IsExistTwoNumsByGcdLcm(gcd, lcm))

    gcd = 100
    lcm = 999
    fmt.Println("gcd =", gcd, ",lcm =", lcm, "。", IsExistTwoNumsByGcdLcm(gcd, lcm))
}

//已知最大公约数和最小公倍数，如何判断这两个数是否存在？
func IsExistTwoNumsByGcdLcm(gcd int, lcm int) bool {

    //1.如果最大公约数或者最小公倍数有小于1的，不存在这两个数。
    if gcd < 1 || lcm < 1 {
        return false
    }

    //2.如果最大公约数等于1，存在这两个数。这个步骤可以不要。
    if gcd == 1 {
        return true
    }

    //3.如果最大公约数大于最小公倍数，不存在这两个数。这个步骤可以不要。
    if gcd > lcm {
        return false
    }

    //4.如果最小公倍数不能被最大公约数整除，不存在这两个数。
    if lcm%gcd != 0 {
        return false
    }

    //5.通过所有考验，一定存在这种两个数。
    return true
}

敲命令 go test -v -test.run TestGcdIsExistTwoNumsByGcdLcm 执行结果如下：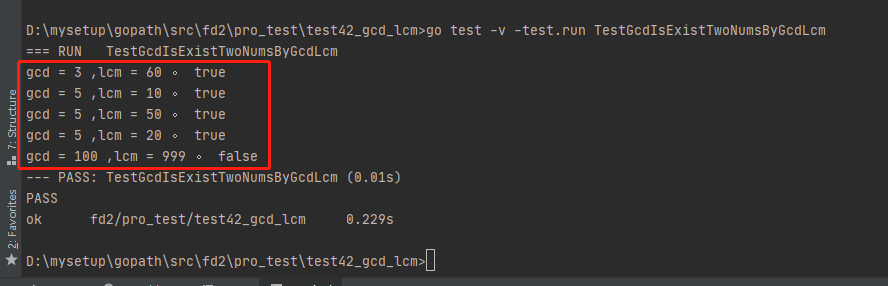

***
[评论](https://user.qzone.qq.com/3182319461/blog/1600642145)