0.PTA得分截图

1.本周学习总结
1.1 总结栈和队列内容
-
栈的存储结构及操作:
- 栈是一种只允许在一端(栈顶)进行插入和删除的线性表。栈有顺序存储和链式存储两种存储结构。栈具有先进后出的特点。
- 栈的顺序存储结构:
//定义顺序栈 typedef struct { int data[MAXSIZE]; int top; }Stack; - 栈的链式存储结构:
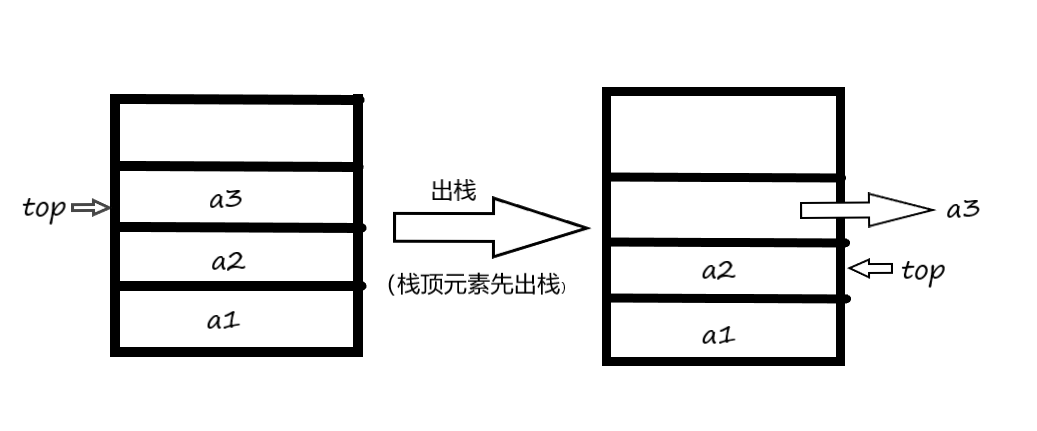
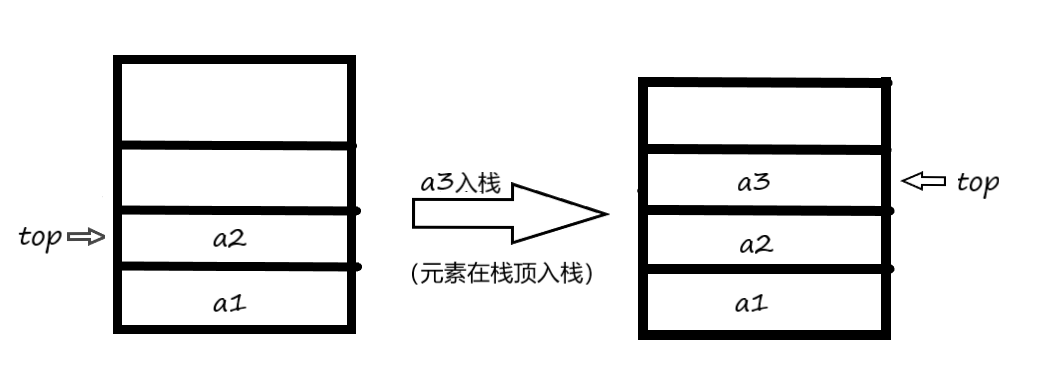
//定义节点 typedef struct SNode { int data; int SNode * next; }SNode,*LinkSNode; //定义栈 typedef struct { LinkSNode top; int size; }Stack; - 栈的出栈与入栈操作:
-
栈的应用:
- 符号配对:判断表达式中的符号是否配对,我们可以利用栈的性质来判断
#include <iostream> #include <stack> #include <stdio.h> #include <map> using namespace std; #define Left symstr[i] == '(' || symstr[i] == '[' || symstr[i] == '{' #define Right symstr[i] == ')' || symstr[i] == ']' || symstr[i] == '}' bool IsMatch(string symstr, char& topc); int main() { string symstr; char topc; cin >> symstr; if (IsMatch(symstr, topc)) { cout << "yes"; } else { if (topc == 0) { cout << "no"; } else { cout << topc << endl << "no"; } } } bool IsMatch(string symstr, char& topc) { int i; int strlen; stack<char> st; strlen = symstr.size(); map<char, char> mp; mp[')'] = '('; mp[']'] = '['; mp['}'] = '{'; for (i = 0; i < strlen; i++) { if (Left) { st.push(symstr[i]); } if (Right) { if (st.empty()) { topc = 0; return false; } topc = st.top(); if (mp[symstr[i]] == topc) { st.pop(); } else { return false; } } } if (st.empty()) { return true; } else { topc = st.top(); return false; } } - 表达式转换:将中缀表达式转换为后缀表达式也可利用栈的性质来实现
#define MaxSize 100 #include <iostream> #include <stack> using namespace std; void TransExpression(char* str,char*expression); int main() { char str[MaxSize]; char expression[MaxSize]; stack<char> st; cin >> str; TransExpression(str,expression); cout << expression; return 0; } void TransExpression(char* str, char *expression) { int i = 0;//遍历str的下标; int j = 0;//转换后的下标; stack<char>st; while (str[i]) { switch (str[i]) { case '(':st.push(str[i]); i++; break; case ')': while(st.top() != '(') { expression[j++] = st.top(); expression[j++] = ' '; st.pop(); } st.pop();//删除栈中的左括号; i++; break; case '+': case '-': if (i == 0||( i!=0 &&str[i-1]=='('))//如果为负数; { if(str[i]=='-') expression[j++] = str[i]; } else { while (!st.empty() && st.top() != '(') { expression[j++] = st.top(); expression[j++] = ' '; st.pop(); } st.push(str[i]); } i++; break; case '*': case '/': if (!st.empty() && (st.top() == '*' || st.top() == '/')) { expression[j++] = st.top(); expression[j++] = ' '; st.pop(); } st.push(str[i]); i++; break; default: while (str[i] <= '9' && str[i] >= '0'||str[i]=='.') { expression[j++] = str[i]; i++; } expression[j++] = ' '; } } while (!st.empty()) { expression[j++] = st.top(); expression[j++] = ' '; st.pop(); } expression[--j] = '�'; }
- 符号配对:判断表达式中的符号是否配对,我们可以利用栈的性质来判断
-
队列的存储结构及操作:
- 队列是一种先进先出的线性表,元素在队头出队,队尾入队。队列也有顺序存储和链式存储两种存储结构。
- 队列的顺序存储结构:
//定义循环队列 typedef struct { int data[MAXSIZE]; int front; int rear; }Queue; - 队列的链式存储结构:
//定义节点 typedef struct QNode { int data; int QNode * next; }QNode,*LinkQNode; //定义链队列 typedef struct { LinkQNode front,rear; int size; }Queue; - 队列的出队与入队操作:

-
队列的应用:
- 迷宫问题:
#include <stdio.h> #define MaxSize 100 #define M 8 #define N 8 int mg[M+2][N+2]= { {1,1,1,1,1,1,1,1,1,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,1,0,0,0,1,0,1}, {1,0,0,0,0,1,1,0,0,1}, {1,0,1,1,1,0,0,0,0,1}, {1,0,0,0,1,0,0,0,0,1}, {1,0,1,0,0,0,1,0,0,1}, {1,0,1,1,1,0,1,1,0,1}, {1,1,0,0,0,0,0,0,0,1}, {1,1,1,1,1,1,1,1,1,1} }; typedef struct { int i,j; //方块的位置 int pre; //本路径中上一方块在队列中的下标 } Box; //方块类型 typedef struct { Box data[MaxSize]; int front,rear; //队头指针和队尾指针 } QuType; //定义顺序队类型 void print(QuType qu,int front) //从队列qu中输出路径 { int k=front,j,ns=0; printf(" "); do //反向找到最短路径,将该路径上的方块的pre成员设置成-1 { j=k; k=qu.data[k].pre; qu.data[j].pre=-1; } while (k!=0); printf("迷宫路径如下: "); k=0; while (k<MaxSize) //正向搜索到pre为-1的方块,即构成正向的路径 { if (qu.data[k].pre==-1) { ns++; printf(" (%d,%d)",qu.data[k].i,qu.data[k].j); if (ns%5==0) printf(" "); //每输出每5个方块后换一行 } k++; } printf(" "); } int mgpath(int xi,int yi,int xe,int ye) //搜索路径为:(xi,yi)->(xe,ye) { int i,j,find=0,di; QuType qu; //定义顺序队 qu.front=qu.rear=-1; qu.rear++; qu.data[qu.rear].i=xi; qu.data[qu.rear].j=yi; //(xi,yi)进队 qu.data[qu.rear].pre=-1; mg[xi][yi]=-1; //将其赋值-1,以避免回过来重复搜索 while (qu.front!=qu.rear && !find) //队列不为空且未找到路径时循环 { qu.front++; //出队,由于不是环形队列,该出队元素仍在队列中 i=qu.data[qu.front].i; j=qu.data[qu.front].j; if (i==xe && j==ye) //找到了出口,输出路径 { find=1; print(qu,qu.front); //调用print函数输出路径 return(1); //找到一条路径时返回1 } for (di=0;di<4;di++) //循环扫描每个方位,把每个可走的方块插入队列中 { switch(di) { case 0:i=qu.data[qu.front].i-1; j=qu.data[qu.front].j;break; case 1:i=qu.data[qu.front].i; j=qu.data[qu.front].j+1;break; case 2:i=qu.data[qu.front].i+1; j=qu.data[qu.front].j;break; case 3:i=qu.data[qu.front].i, j=qu.data[qu.front].j-1;break; } if (mg[i][j]==0) { qu.rear++; //将该相邻方块插入到队列中 qu.data[qu.rear].i=i; qu.data[qu.rear].j=j; qu.data[qu.rear].pre=qu.front; //指向路径中上一个方块的下标 mg[i][j]=-1; //将其赋值-1,以避免回过来重复搜索 } } } return(0); //未找到一条路径时返回1 } int main() { mgpath(1,1,M,N); return 1; }
- 迷宫问题:
-
栈和队列的共同点:都只能在线性表的端点进行插入和删除操作,不能直接对中间的数据进行操作。
1.2 谈谈你对线性表的认识及学习体会
在本章栈和队列的学习中,感觉对于栈和队列的理解其实并不难,但是在应用的时候却有些困难,不知道该如何利用栈和队列去解决问题。而且刷pta时,题目有明确用哪个方法去解题,但是之后如果需要自己去写代码的话,可能就不知道什么时候该利用栈和队列了。希望自己可以多看些栈和队列的应用,早日熟悉利用栈和队列去解决问题。
2.PTA实验作业
2.1 银行业务队列简单模拟
2.1.1 代码截图
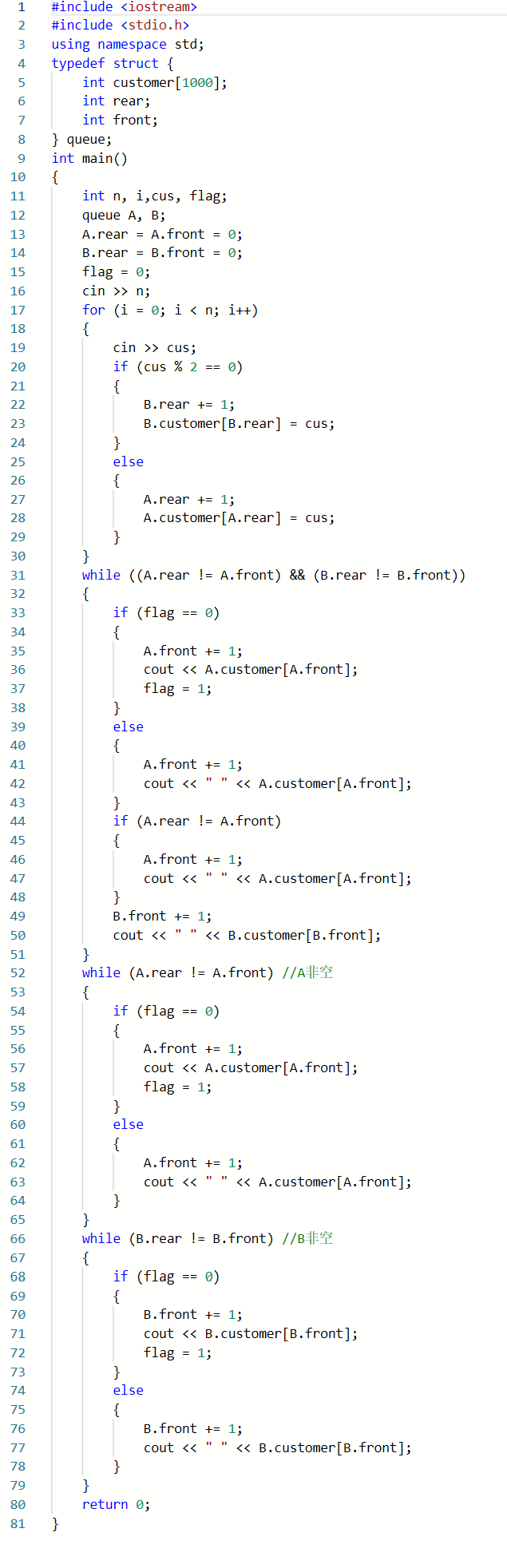
2.1.2 PTA提交列表及说明

2.2 表达式转换
2.2.1 代码截图

2.2.2 PTA提交列表及说明

1. 多种错误:一开始我的代码只支持个位数的运算,如果是多位数,数字之间会出现空格
2.部分正确:修改了数字的输出,让程序可以输出多位数
3.答案正确:因为之前的代码一直改都不对,所以最后还是用了课件上的思路
3.阅读代码
3.1 验证栈序列
题目:
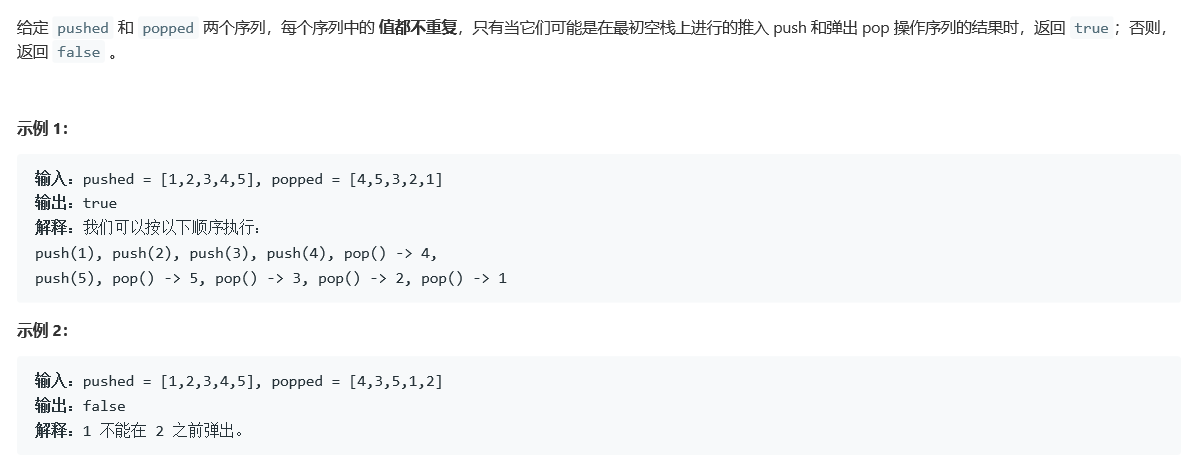
解题代码:
bool validateStackSequences(int* pushed, int pushedSize, int* popped, int poppedSize)
{
if (pushed == NULL || pushedSize < 0 || popped == NULL || poppedSize < 0) {
return false;
}
if (pushedSize > 1000 || poppedSize > 1000) {
return false;
}
int tmpStack[1000] = { 0 };
int tmpStackTop = -1;
int pushedIter = 0;
int poppedIter = 0;
while (pushedIter < pushedSize) {
// 入栈一个数
tmpStack[++tmpStackTop] = pushed[pushedIter++];
// 当前栈顶如果和pop当前位置相同,则出栈
while (tmpStackTop >= 0 && poppedIter < poppedSize && tmpStack[tmpStackTop] == popped[poppedIter]) {
// 出栈后,栈顶下移,pop序列增加
tmpStack[tmpStackTop--] = 0;
poppedIter++;
}
}
// 最终栈底回到-1位置,否则没有完全匹配
if (tmpStackTop != -1) {
return false;
}
return true;
}
3.1.1 该题的设计思路
当入栈的栈顶等于要出栈的第一个数时,让栈顶元素出栈,然后继续与要出栈的元素比较,若相等则继续比较,若不等则让后续元素继续入栈,重复上述步骤。
3.1.2 该题的伪代码
while(pushed的下标 < pushed的长度)
{
入栈一个数
while(当前栈顶元素与pop当前位置元素相同)
{
出栈一个元素,pop下标增加;
}
}
最终栈底回到-1位置,否则没有完全匹配
3.1.3 运行结果


3.1.4 分析该题目解题优势及难点
难点:元素并不是一次性入栈的,有可能在半中间就会先出栈,要根据出栈顺序来判断。
解题优势:用两个while循环就解决了问题,代码清晰简洁,容易理解。
3.2 根据身高重建队列
题目:

解题代码:
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
// 排序
sort(people.begin(), people.end(),
[](const vector<int>& lhs, const vector<int>& rhs)
{return lhs[0] == rhs[0] ? lhs[1] <= rhs[1] : lhs[0] > rhs[0];});
int len = people.size();
list<vector<int>> tmp;
// 循环插入
for(int i = 0; i < len; ++i){
auto pos = tmp.begin();
advance(pos, people[i][1]);
tmp.insert(pos, people[i]);
}
// 重建vector返回
return vector<vector<int>>(tmp.begin(), tmp.end());
}
3.2.1 该题的设计思路
先排身高更高的,这是要防止后排入人员影响先排入人员位置。每次排入新人员[h,k]时,已处于队列的人身高都>=h,所以新排入位置就是people[k]
3.2.2 该题的伪代码
现将身高按降序排列
for i=0 to i<len do
auto pos = tmp.begin();
advance(pos, people[i][1]);
tmp.insert(pos, people[i]);
end for
重建vector返回
3.2.3 运行结果

3.1.4 分析该题目解题优势及难点
难点:不是简单的排序身高,还要考虑到前面需要有几个人的身高比当前的高
解题优势:因为个子矮的人相对于个子高的人是 “看不见” 的,所以可以先安排个子高的人。再根据k值进行插入,将复杂问题简单化,思路也容易理解。