考虑这样一个问题:$n imes m$的平面上有k个点(坐标都是整数),求一个面积最大的边平行于坐标轴的矩形,使得其内部不包含任何一个给出的点(但是可以在边界上)。就比如说下面这幅图:
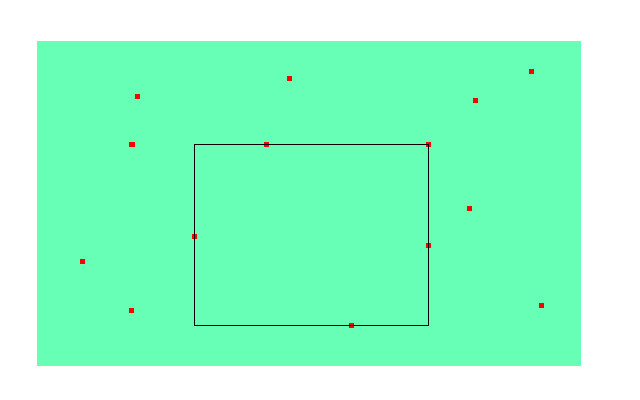
红色的点是给出的点,那么黑色框框表示的这个矩形就是要求的最大子矩形啦。
最暴力的做法:提前预处理出一个二维部分和,然后枚举左上角的顶点和右下角的顶点每次判断是否合法并用面积更新答案就可以了。复杂度是$O(n^2m^2)$的。这太大了,不好接受。
考虑进行优化。
假如现在我们定下来上下两条边界,枚举右边界,那么向左一定会延伸到第一个障碍点(否则一定不是最优的)。那么我们省去了一维枚举,复杂度可以降为$O(n^nm)$
但是这还是不够爽啊,我们希望得到的复杂度是$O(nm)$。
既然这样,我们只有两种思路:枚举两个边界,然后每次用常数的时间求出最优解,或是枚举一侧边界,每次用$O(n)$的时间求出最优解。考虑第一种思路。如果枚举的是相对的两侧的话,那么刚刚我们已经找到了$O(n)$找出最优解的方法,很难想到更优的方法。那么就试图枚举相邻的两侧(右侧和上侧)。套用刚刚的想法,我们试图找到左下角最近的障碍。但由于是二维的状态,所以问题变得很困难,GG
那么只剩下枚举一条边界的思路的。假设我们枚举的是上边界。由于枚举的维数变少,所以我们希望预处理得到的信息更多。考虑一下关于每条上边界,我们能预处理出什么。很显然的我们可以轻松地得到边界上每个点向下最远延伸多少,像下图这样:
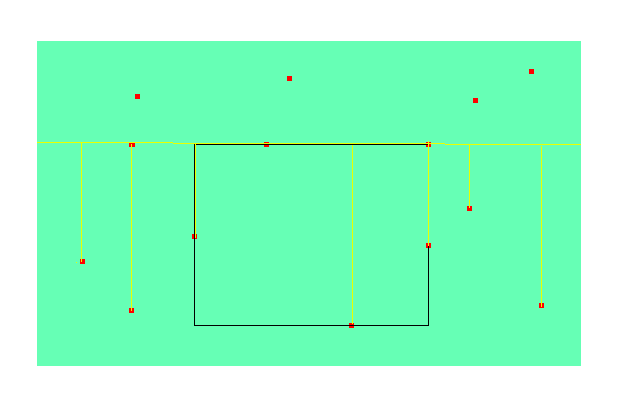
黄线是我们枚举的上边界。延伸下来的就是它能延伸的最下方(没画出来的位置表示可以一直延伸到图形底端)。这个东西可以很容易预处理出来。如果左右边界确定的话,下边界一定是这一段里向下延伸距离最小的了。那么问题就变成了$O(n)$的时间求出一段数中最大的长度*RMQ。用单调栈可以预处理出每个数左边第一个比它小的和右边第一个比它小的。具体做法是这样的:维护一个单调递增的栈,每次进栈时的原栈顶就是答案,时间复杂度$O(n)$。然后只需要枚举RMQ是哪个就可以了,再乘以它左右延伸的长度。
总结:这个东西我们用到的最主要的性质就是坐标有界且都是整数。考虑通过预处理来减少枚举的维数,从最初的暴力逐步优化成一个$O(n^2)$的优秀算法。
例题:BZOJ1057棋盘制作:
题目大意:给出一个n*m的黑白棋盘,求出一个面积最大的子矩形和面积最大的子正方形使得它们内部相邻的两格不同色。
第一步是求出一个标准的棋盘(n*m且相邻两格不同色的棋盘),然后将给出的棋盘与之异或。(这样可以放在一起的就变成了一块连续的1或0),然后问题就化归为了上面的模型。面积最大的子正方形只需要求出所有合法矩形中较小边最大的那个就行了。

1 //date 20140703 2 #include <cstdio> 3 #include <cstring> 4 5 const int maxn = 2050; 6 7 inline int getint() 8 { 9 int ans(0); char w = getchar(); 10 while(w < '0' || '9' < w) w = getchar(); 11 while('0' <= w && w <= '9') {ans = ans * 10 + w - '0'; w = getchar();} 12 return ans; 13 } 14 15 inline int innew(int &a, int b){if(a < b){a = b; return 1;} return 0;} 16 inline int min(int a, int b){return a < b ? a : b;} 17 18 int n, m; 19 int map[maxn][maxn], down[maxn][maxn], stack[maxn], lft[maxn], rgt[maxn]; 20 int anssqr, ansrec; 21 22 int main() 23 { 24 n = getint(); m = getint(); 25 anssqr = ansrec = 0; 26 for(int i = 1; i <= n; ++i) for(int j = 1; j <= m; ++j) map[i][j] = ((i ^ j) & 1) ^ getint(); 27 28 /* for(int i = 1; i <= n; ++i) 29 { 30 for(int j = 1; j <= m; ++j) printf("%d ", map[i][j]); 31 printf(" "); 32 } 33 printf(" ");*/ 34 //calc 0 35 memset(down, 0, sizeof down); 36 for(int i = 1; i <= m; ++i) down[n][i] = !map[n][i]; 37 for(int i = n - 1; i; --i) for(int j = 1; j <= m; ++j) if(!map[i][j]) down[i][j] = down[i + 1][j] + 1; 38 39 /* for(int i = 1; i <= n; ++i) 40 { 41 for(int j = 1; j <= m; ++j) printf("%d ", down[i][j]); 42 printf(" "); 43 } 44 printf(" "); 45 */ 46 for(int i = 1; i <= n; ++i) 47 { 48 int stop = 0, lastzero = 0; 49 for(int j = 1; j <= m; ++j) 50 { 51 if(!down[i][j]){lastzero = j; stop = 0; continue;} 52 while(stop && down[i][stack[stop]] >= down[i][j]) --stop; 53 lft[j] = stop ? stack[stop] : lastzero; 54 stack[++stop] = j; 55 } 56 stop = 0; lastzero = m + 1; 57 for(int j = m; j; --j) 58 { 59 if(!down[i][j]){lastzero = j; stop = 0; continue;} 60 while(stop && down[i][stack[stop]] >= down[i][j]) --stop; 61 rgt[j] = stop ? stack[stop] : lastzero; 62 stack[++stop] = j; 63 } 64 65 // for(int j = 1; j <= m; ++j) printf("%d ", lft[j]); printf(" "); 66 // for(int j = 1; j <= m; ++j) printf("%d ", rgt[j]); printf(" "); 67 68 for(int j = 1; j <= m; ++j) if(down[i][j]) 69 { 70 innew(ansrec, down[i][j] * (rgt[j] - lft[j] - 1)); 71 innew(anssqr, min(down[i][j], (rgt[j] - lft[j] - 1))); 72 } 73 } 74 75 // printf("%d %d ", anssqr * anssqr, ansrec); 76 77 //calc 1 78 79 memset(down, 0, sizeof down); 80 for(int i = 1; i <= m; ++i) down[n][i] = map[n][i]; 81 for(int i = n - 1; i; --i) for(int j = 1; j <= m; ++j) if(map[i][j]) down[i][j] = down[i + 1][j] + 1; 82 83 /* 84 for(int i = 1; i <= n; ++i) 85 { 86 for(int j = 1; j <= m; ++j) printf("%d ", down[i][j]); 87 printf(" "); 88 } 89 printf(" "); 90 */ 91 for(int i = 1; i <= n; ++i) 92 { 93 int stop = 0, lastzero = 0; 94 for(int j = 1; j <= m; ++j) 95 { 96 if(!down[i][j]){lastzero = j; stop = 0; continue;} 97 while(stop && down[i][stack[stop]] >= down[i][j]) --stop; 98 lft[j] = stop ? stack[stop] : lastzero; 99 stack[++stop] = j; 100 } 101 stop = 0; lastzero = m + 1; 102 for(int j = m; j; --j) 103 { 104 if(!down[i][j]){lastzero = j; stop = 0; continue;} 105 while(stop && down[i][stack[stop]] >= down[i][j]) --stop; 106 rgt[j] = stop ? stack[stop] : lastzero; 107 stack[++stop] = j; 108 } 109 // for(int j = 1; j <= m; ++j) printf("%d ", lft[j]); printf(" "); 110 // for(int j = 1; j <= m; ++j) printf("%d ", rgt[j]); printf(" "); 111 112 for(int j = 1; j <= m; ++j) if(down[i][j]) 113 { 114 innew(ansrec, down[i][j] * (rgt[j] - lft[j] - 1)); 115 innew(anssqr, min(down[i][j], (rgt[j] - lft[j] - 1))); 116 } 117 } 118 119 printf("%d %d ", anssqr * anssqr, ansrec); 120 return 0; 121 }
