KMP算法

看到一篇写的特别好的KMP blog：https://www.cnblogs.com/zzuuoo666/p/9028287.html

简单模式匹配算法

对于一个串中某子串的定位操作称为模式匹配

	int i=1,j=1,k=i;  //从主串和模式串第一个位置开始遍历 
	while(i <= s_length && j <= t_length){
		if(s[i]==t[j]){//如果相等,则都向后进一位 
			++i;
			++j;
		}
		else{         //如果不相等，则 i 回溯到下一位，j 回溯到模式串第一位，重新依次比较 
			j=1;
			i=++k;   //或写为i=i-j+2;
		}
	}
	if(j > t_length)cout<<k<<endl;
	else cout<<"NO"<<endl; 

KMP算法

简单模式匹配算法需要不断回溯主串和子串，但是KMP算法只需要回溯子串，这就是它更快的原因

原来需要将子串回溯到下标为1，将主串回溯到下一位，KMP算法只需要将子串下标 j 回溯到 next[j] 的位置，所以求next数组就是它的核心
出现了几个个问题：
1.next数组存的是什么？ 为什么只用将子串下标 j 回溯到 next[j]的位置就能达到我们想要的效果？
2.怎么求next数组。
1.next[j]数组存的是如果主串和子串失配，j要回溯的那个位置

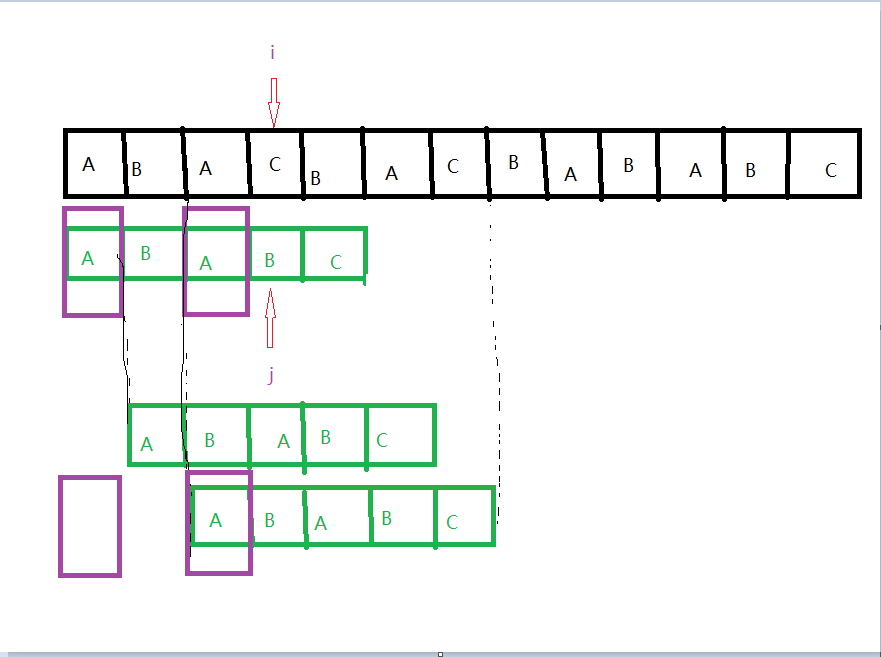
如图，如果按照原来的方法，主串和子串都需要回溯比较，但是我们发现有一些比较其实是可以省略的，观察图中，发现
a.比较下标前面的子串完全匹配。
b.前面的子串存在相同的前后缀（紫色框中），且为最长的相等前后缀
根据这两点，我们就可以直接将子串从第一个框位置移动到第二个框位置去比较，中间部分不存在完全匹配的可能。
因为现在j下标失配（不相等），我们要使主串子串完全匹配，就需要向右移动子串，因为紫色框为与前缀相同的最长后缀，所以中间不可能存在与主串匹配的部分，即使存在也会发生断层，否则紫色框就不是与前缀相等的最长后缀了，就矛盾了。

求next数组

void get_next(char *t , int *next){
	int i,j;
	i=1;
	j=0;
	next[1]=0;
	while(i<t_length){
		if(j==0||t[i]==t[j]){
			++i;
			++j;
			next[i]=j;//如果相等 next[i+1]相当于next[i]+1;
		}
		else j=next[j];//否则，j回溯，直到相同或 j 为0 ，就是缩短前后缀 
	}
}

KMP

	get_next(t,next);
	int i=1;//若从pos位置匹配i=pos;
        j=1;
	while(i <= s_length && j <= t_length){
		if(j==0||s[i]==t[j]){
			++i;
			++j;
		}
		else{
			j=next[j];//修改了这里
		}
	} 
	if(j > t_length)cout<<i-j+1<<endl;
	else cout<<"NO"<<endl; 

优化KMP，求nextval数组

void get_nextval(char *t , int *nextval){
	int i,j;
	i=1;
	j=0;
	nextval[1]=0;
	while(i<t_length){//t_length为模式串的长度 
		if(j==0||t[i]==t[j]){
			++i;
			++j;
			if(t[i]!=t[j])    //相同就继续回溯 
				nextval[i]=j;
			else
				nextval[i]=nextval[j];
		}
		else j=nextval[j];
	}
}