introduction
Assumption
热分布模型
画出不同个数加热管的热量分布
角度问题
Super pan model
第一部分
第二部分
第三部分
结论
优缺点
优点
缺点
名词
蒙特卡罗(Monte Carlo)方法
水纹效应
题目
summary
两个目标:
热量的正态分布
最优化烤盘设置
两个模型:
分析和最优化
第一个模型:
总体和局部方法来观察每个盘的受热情况
- 斯特藩-玻尔兹曼定律(stefan-boltzmann)和傅立叶定理来刻画空气的热分布和电加热管
- 分析XX拦截和改良的蒙特卡罗算法
然后不同盘子的受热就知道了
第二个模型:
离散化转换方法来接近最优化的烤箱形状和数量
最后细化比重p
特点:
Durex的方法来转化变量——从整个空间到局部地区——可以刻画热量分布
introduction
- 我们研究热辐射而不是热传导——避免复杂的公式
- 巧妙将总体变量转化为局部变量
Assumption
- 两层,均匀分布
- 所有欧安的材料一样
- 烤箱内部墙是一个黑体——不反射热量
热分布模型
四步:
- 傅里叶准则——计算热量损失——每个加热管周围的热量分布
- 当放入烤盘的时候,整个热量地图就会被烤盘穿过——可以得到烤盘的热量分布
- 建立合适的模型来得到烤盘的每个点的反射情况——简化的蒙特卡罗算法
——得到没有反射损失的烤盘热量分布 - 得到实际的结论——将我们的模型和水纹传播现象
论文的第一步会介绍一下发热管的厨师热量
画出不同个数加热管的热量分布
没有烤盘的情况
一个两个

放入一个盘:
方形
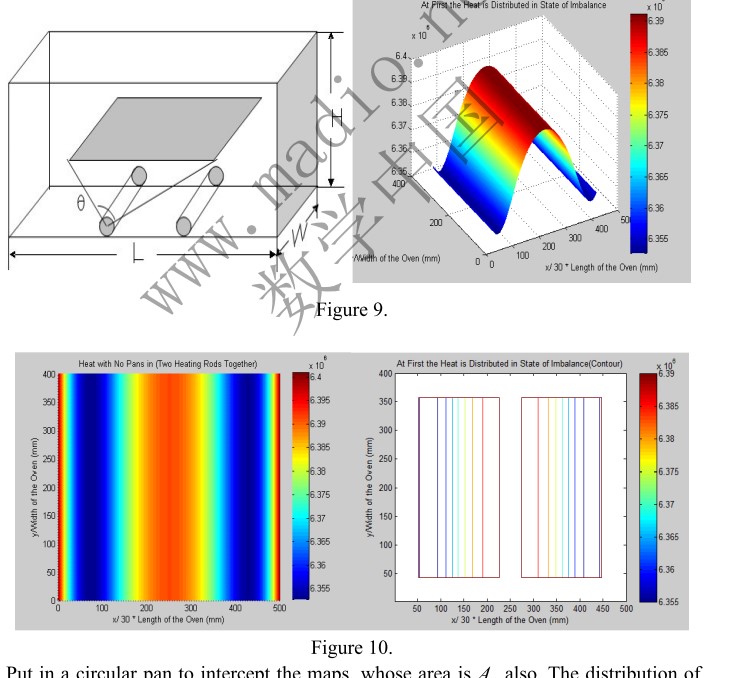
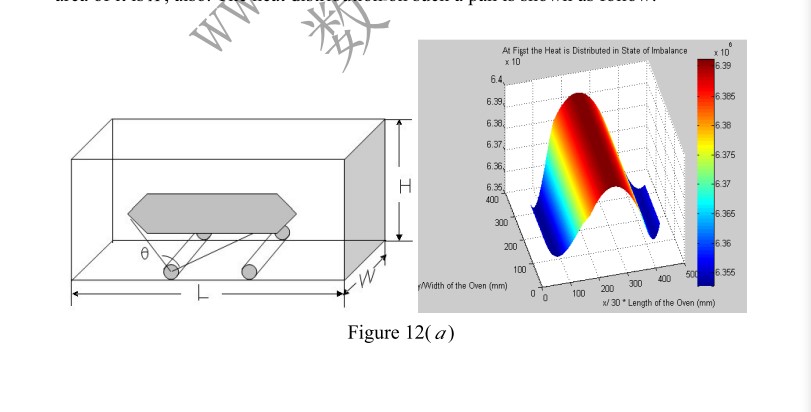
圆形:

菱形:
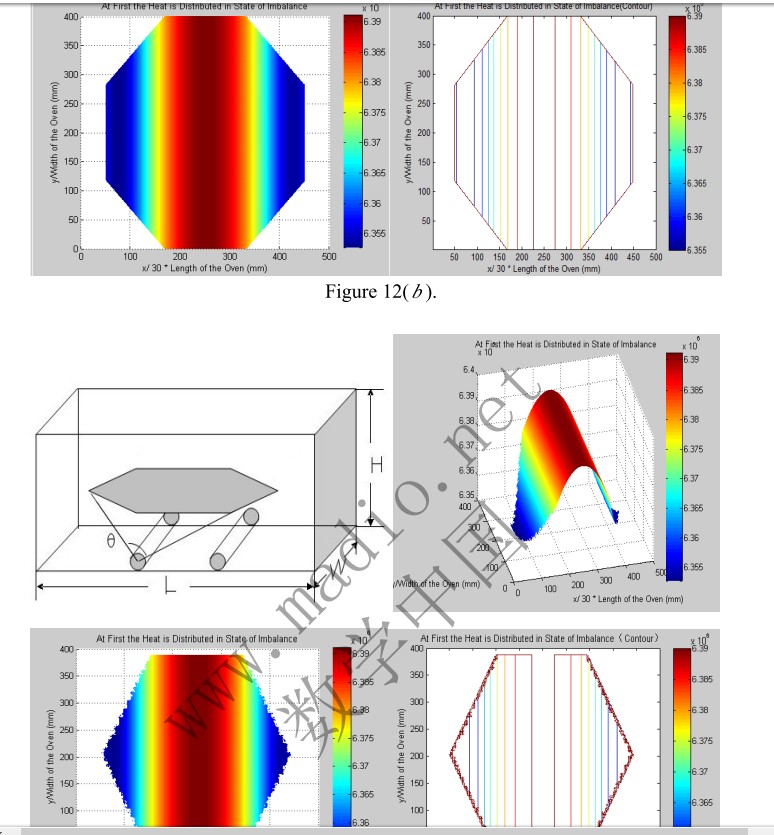
角度问题
门特卡罗模拟
选择0~1中的随机数——反射率
- 建立一个模型
角度——从电子加热管的角度看
越圆越受热均匀
要使加热均匀,盘的边越少越好
Super pan model
假设:
宽度:100mm
最多三个盘子
每个盘的面积是A
第一部分
最多的盘子个数
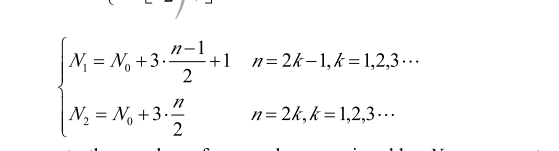
第二部分
计算长宽比——Maximum the heat distribution of the pans.
第三部分
前面的两个:一个是最大的平均热量,另一个是计算可以放的最多的盘子——不能达到平均
综合plan1和plan2——引入P
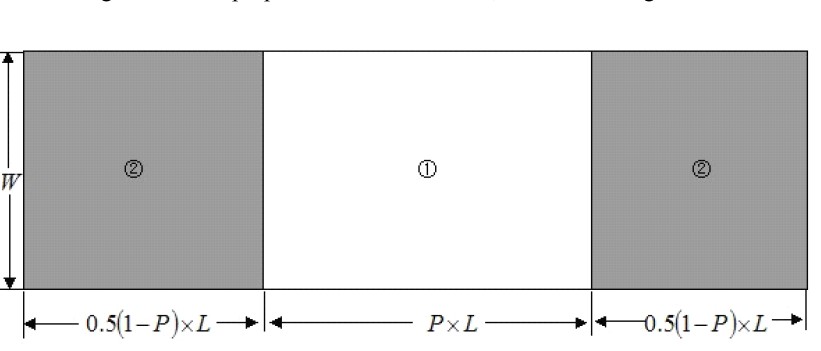
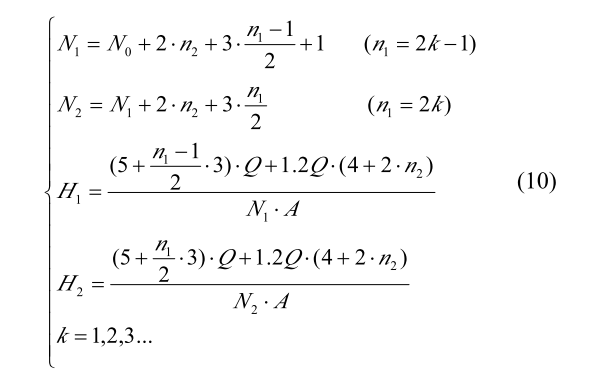
不同的长宽比的结果不同
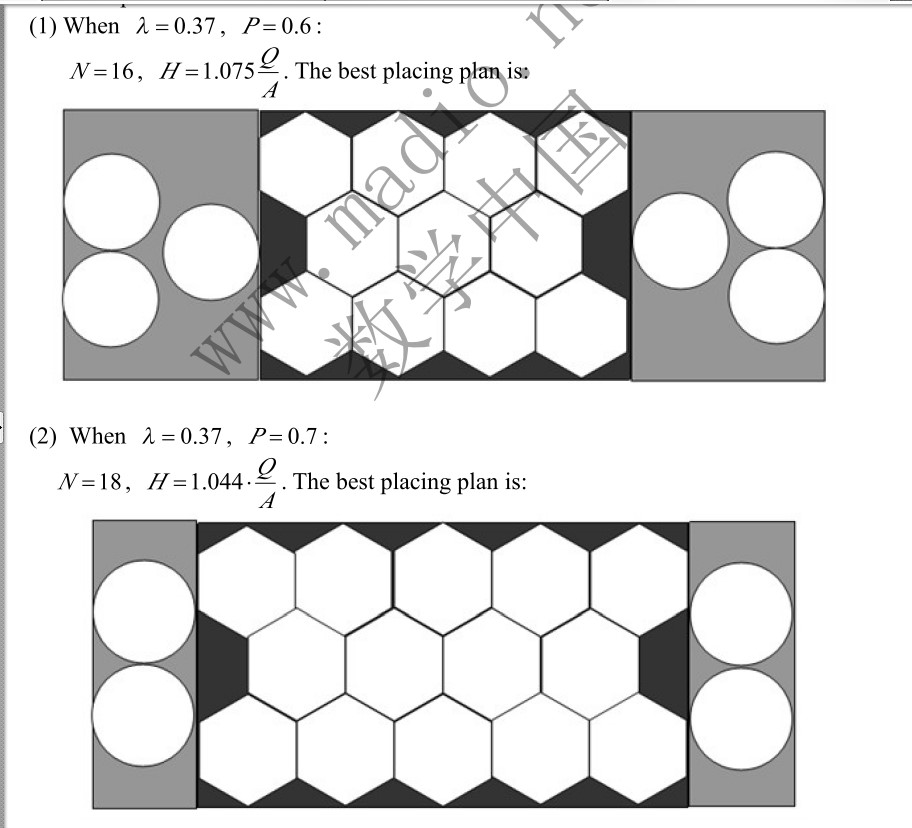
结论
- 越多的边,加热越均匀
- 通过离散转变方法,当长宽比一定,随着P增加,盘子增多,但是平均温度减少——要根据实际需求定
优缺点
优点
- 避免困难
- 贴近实际
- 灵活性
- 创新性
the space of an oven can be divided into six parts
缺点
- 烤盘的热传导忽略了
- 电加热管的热传导忽略了
- 线性简化
名词
蒙特卡罗(Monte Carlo)方法
又称随机抽样或统计试验方法,属于计算数学的一个分支,它是在上世纪四十年代中期为了适应当时原子能事业的发展而发展起来的。传统的经验方法由于不能逼近真实的物理过程,很难得到满意的结果,而蒙特卡罗方法由于能够真实地模拟实际物理过程,故解决问题与实际非常符合,可以得到很圆满的结果。
当所要求解的问题是某种事件出现的概率,或者是某个随机变量的期望值时,它们可以通过某种“试验”的方法,得到这种事件出现的频率,或者这个随机变数的平均值,并用它们作为问题的解。这就是蒙特卡罗方法的基本思想。蒙特卡罗方法通过抓住事物运动的几何数量和几何特征,利用数学方法来加以模拟,即进行一种数字模拟实验。它是以一个概率模型为基础,按照这个模型所描绘的过程,通过模拟实验的结果,作为问题的近似解。可以把蒙特卡罗解题归结为三个主要步骤:构造或描述概率过程;实现从已知概率分布抽样;建立各种估计量。
水纹效应
是网络传播学中典型的一种传播模型,就像在平静的湖水中扔下一颗石子,水纹就会以很快的速度向周围产生共振波,扩散的范围和效果受到水质和水面地形的影响而有所不同。
同样,在网络传播学中,信息的扩散效应也会有这种类似的扩散模型,而建立这种扩散模型要有以下几个必要条件才能形成扩散:
1.作为石子基点的自己所处的位置,要有水域,也就是可以与你产生共鸣的许多水质基点,石子基点和每个水质基点间要有良好的信息沟通和共享能力,并且石子基点最重要的特点就是可以自由获得信息。
2.石子基点要有个合适的石子,也就是能让水质基点产生共鸣和认同的信息,而这个石子的来源也一定要值得认可。
3.在信息扩散时,信息通信渠道不应当有任何破坏信息完整性的因素存在。
4.每个基点,包括石子基点和水质基点都要有完整的独立判断和转发能力,能有自我决定转发自己喜好信息的能力
基于以上几个必要因素,我们就建立了一个水纹传播模型,而这里要说明的一点是,并非石子基点和水质基点是始终不变的,因为他们每个基点都有独自转发信息的能力和获取信息的能力,所以每个基点都可以作为石子基点或水质基点,而此时我们会发现,当一个基点既作为石子基点又同时作为水质基点时,我们可以认为这个水纹模型已经干涸,换个意思说就是这个水纹模型已经没有使用价值了。
题目
当在一个矩形的锅烘烤时热量会在4个角落集中,并使产品在拐角
处(以及在较小程度上在边缘处)加热过度。在一个圆形盘的热量
被均匀地分布在整个外缘并且在边缘处的产品不会加热过度。然而
,相对于使用的空间的烘箱中,由于大多数烤炉是矩形的形状使用
圆形平底锅是效率不高。
开发一个模型来显示不同形状的平底锅锅的外边缘之间的热分布-
矩形到圆形和在两者之间的其它形状。
假设
1。烘箱是矩形的形状,宽度长度比为W / L,定名为A;
2。在A中,每盘必须有一个区域。
3。最初两个烘烤架均匀地间隔开。
开发模型,使其在下列条件下可用于选择的最佳类型的盘(形状):
1。锅数量最大情况并适合烤箱的锅形状(N)
2。使锅的热量最大化均匀分布(H)的锅形状
3。优化的组合的条件(1)和(2)式中的权重p和(1 - p)被分
配的结果来说明,W / L 和 p的 不同的值的变化。
在除了您的MCM格式化论文外,制备一到两页的广告单,发到布朗
尼美食杂志,注意突出您的设计和结果。