机器学习：逻辑回归（基础理解）

逻辑回归（Logistic Regression）

一、行业算法应用率

• 机器学习算法的本质就是求出一个函数 ý = f(x)，如果给函数输入一个样本 x ，经过 f(x) 运算后得到一个 ý；

• 具统计，2017年，除了军事和安全领域，逻辑回归算法是在其它所有行业使用最多了一种机器学习算法；
• 
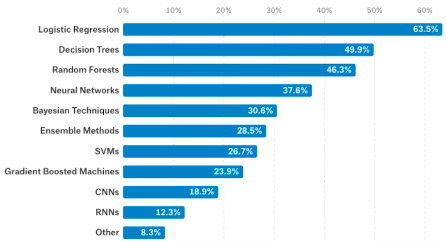
• Logistic Regression（逻辑回归）
• Decision Trees（决策树）
• Random Forests（随机森林）
• Neural Networks（人工神经网络 NNs）——深度学习算法

1. 人工神经网络（Artificial Neural Networks，简写为ANNs）也简称为神经网络（NNs）或称作连接模型（Connection Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。

• Bayesian Techniques（贝叶斯）
• Ensemble Methods（集成算法）
• SVMs（SVM 算法）
• Gradient Boosted Machines（梯度提升机）
• CNNs（卷积神经网络）——深度学习算法
• RNNs（递归神经网络）——深度学习算法

• 机器学习算法并不是越复杂越好，要根据实际使用的场景选择最合适的算法；因此，脱离实际应用场景，并没有一种算法比另一种算法更好；

• 使用深度学习算法时，对数据量和计算能力要求非常高，需要非常大的数据量，面对数据量较少的应用，使用简单的算法会达到更好的效果。

二、简介

• 逻辑回归算法是从线性回归算法衍生而来

　1）逻辑回归算法解决分类问题

• 原理：将样本的特征和样本发生的概率联系起来，预测样本发生的概率，然后根据概率进行分析；（这也是与其它算法的不同点）
• 

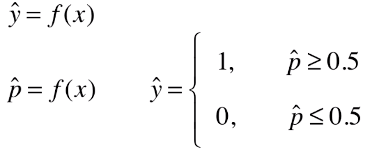
• 逻辑回归既可以看做回归算法，也可以看做是分类算法；

1. 如果模型只预测样本发生的概率，是一个数，可称该算法为回归算法；
2. 如果预测出样本发生的概率后，再根据概率对样本做进一步确认，则可称该算法为分类算法；

• 通常逻辑回归作为分类算法使用，但是只可以解决二分类问题；（当然也可以进行改进，使得逻辑回归算法可以解决多分类问题）

　2）逻辑回归算法的由来

• 线性回归 / 多项式回归的问题：预测结果的可信度比较差；

1. 原因：在线性回归算法中，对一个样本的预测值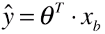： （如果同时对 m 个样本预测：X_b .θ^T），只看数学模型代数式，预测值 ý 的取值范围：(-∞，+∞)，理论上可以通过线性回归的方式求得任意的值，所以直接使用线性回归的方式，找到一组 θ 与 X_b 相乘，结果最为预测值；单从应用的角度来讲，可以这么做，但是这样做的效果不够好，因为预测值 ý 没有值域的限制，使得有线性回归拟合的直线或者有多项式回归拟合的曲线的可信度较差。

• 解决方案：

1. 不直接根据样本 x 预测 y 值，而是根据样本 x 可能发生的概率来判断可能的 y 值；

• 模型推导：

1. 由于： ，，
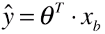2. 所以 ：

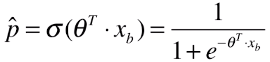
• x_b ：表示待预测的一个或多个样本；
• t：新的模型函数 Ó(t) 的参数，这里指 ý ；
• 将线性模型预测的结果，放在另一个模型函数中，将线性模型预测的结果转换成范围在 [0, 1] 的值，该值做为被预测的样本的发生的概率；

　3）绘制并理解：

• import numpy as np
  import matplotlib.pyplot as plt
  
  def sigmoid(t):
      return 1 / (1 + np.exp(-t))
  
  x = np.linspace(-10, 10, 500)
  y = sigmoid(x)
  
  plt.plot(x, y)
  plt.show()

• 

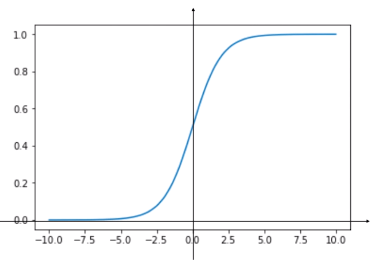
1. 曲线的值域：[0, 1]；
2. 当 t 取 -∞ 时，p 趋近于 0 ，当 t 取 + ∞ 时，p 趋近于1；
3. 当 t > 0 时，p > 0.5，当 t < 0 时，p < 0.5 ；
4. 当 t = 0 时，p = 0.5；
5. np.exp(-t)：表示 e^-t ；

　4）怎么根据样本发生的概率进行分类？

• 
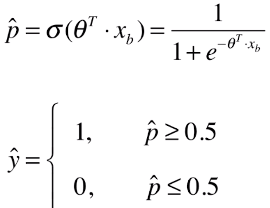
• 举例：预测病人患良性肿瘤还是恶性肿瘤。

1. 模型训练得到超参数 θ ；
2. 将待预测的病人的信息输入给模型，得到该病人患恶性肿瘤的概率；
3. 如果该病人患恶性肿瘤的概率：p ≥ 0.5，则推断该病人很有可能是恶性肿瘤患者；如果该病人患恶性肿瘤的概率：p ≤ 0.5，则推断该病人很有可能是良性肿瘤患者；

　5）问题

• 给定了样本数据集 X 及其对应的分类结果 y，怎么找到参数 θ 使得用这样的方式，可以最大程度获得样本数据集 X 对应的分类输出 y？
• （怎么让模型最大程度拟合训练数据集）

1. 因为要首先求出一组 θ 值，根据此逻辑回归模型，使得在训练数据集上有更好的表现，也就是所谓的拟合训练数据集，但是由于逻辑回归解决分类问题，因此不好判定预测结果的好坏。