机器学习：模型泛化（LASSO 回归）

一、基础理解

• LASSO 回归（Least Absolute Shrinkage and Selection Operator Regression）是模型正则化的一定方式；
• 功能：与岭回归一样，解决过拟合或者模型含有的巨大的方差误差的问题；

二、LASSO 回归

•  以线性回归为例

　1）对于岭回归

• 任务：让最小化的损失函数对应的 θ 值尽量的小；
• 操作：在损失函数中添加了一项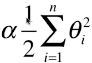：；希望在最小化损失函数时通过添加的此项代数式来控制参数 θ 的大小，并且为了平衡新的损失函数中的两项代数式对损失函数的影响，在添加的代数式中加入了新的参数 α；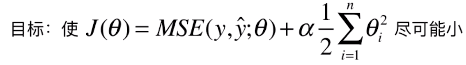
• 

　2）对于 LASSO 回归

• LASSO 回归的原理和岭回归是一样的，只是添加的代数式不同；
• 

三、模拟数据使用 LASSO 回归

　1）模拟数据集

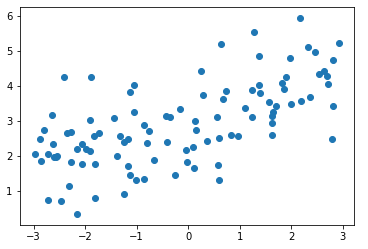
• 模拟并绘制数据集

  import numpy as np
  import matplotlib.pyplot as plt
  
  np.random.seed(42)
  x = np.random.uniform(-3.0, 3.0, size=100)
  X = x.reshape(-1, 1)
  y = 0.5 * x + 3. + np.random.normal(0, 1, size=100)
  
  plt.scatter(x, y)
  plt.show()

  

• 分割数据集

  from sklearn.model_selection import train_test_split
  
  np.random.seed(666)
  X_train, X_test, y_train, y_test = train_test_split(X, y)

　2）使用多项式回归拟合数据

• 管道

  from sklearn.pipeline import Pipeline
  from sklearn.preprocessing import PolynomialFeatures
  from sklearn.preprocessing import StandardScaler
  from sklearn.linear_model import LinearRegression
  
  def PolynomialRegression(degree):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std_scaler', StandardScaler()),
          ('lin_reg', LinearRegression())
      ])

• 封装绘制代码

  def plot_model(model):
      X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
      y_plot = model.predict(X_plot)
  
      plt.scatter(x, y)
      plt.plot(X_plot[:, 0], model.predict(X_plot), color='r')
      plt.axis([-3, 3, 0, 6])
      plt.show()

• 多项式回归并绘图

  from sklearn.metrics import mean_squared_error
  
  poly_reg = PolynomialRegression(degree=20)
  poly_reg.fit(X_train, y_train)
  
  y_poly_predict = poly_reg.predict(X_test)
  mean_squared_error(y_test, y_poly_predict)
  # 输出：167.9401086729357（均方误差）
  
  plot_model(poly_reg)

  

　3）使用 LASSO Regression 改进算法模型

• 管道

  from sklearn.linear_model import Lasso
  
  # 以管道的方式，使用 LASSO 回归的方法改进多项式回归的算法
  def LassoRegression(degree, alpha):
      return Pipeline([
          ('poly', PolynomialFeatures(degree=degree)),
          ('std_scaler', StandardScaler()),
          ('lasso_reg', Lasso(alpha=alpha))
      ])

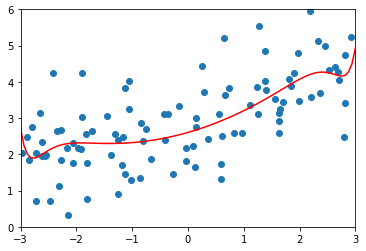
• degree = 20、α = 0.01

  lasso1_reg = LassoRegression(20, 0.01)
  lasso1_reg.fit(X_train, y_train)
  
  y1_predict = lasso1_reg.predict(X_test)
  mean_squared_error(y_test, y1_predict)
  # 输出：1.149608084325997（均方误差）
  
  plot_model(lasso1_reg)

  

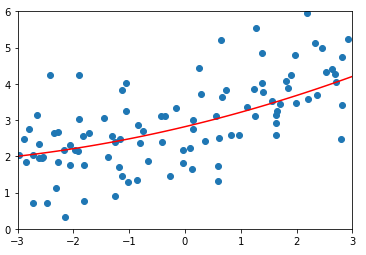
• degree = 20、α = 0.1

  lasso2_reg = LassoRegression(20, 0.1)
  lasso2_reg.fit(X_train, y_train)
  
  y2_predict = lasso2_reg.predict(X_test)
  mean_squared_error(y_test, y2_predict)
  # 输出：1.1213911351818648（均方误差）
  
  plot_model(lasso2_reg)

  

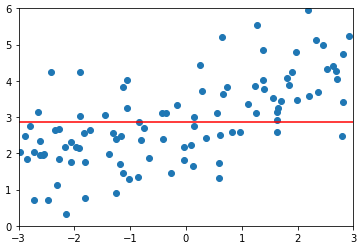
• degree = 20、α = 1

  lasso3_reg = LassoRegression(20, 1)
  lasso3_reg.fit(X_train, y_train)
  
  y3_predict = lasso3_reg.predict(X_test)
  mean_squared_error(y_test, y3_predict)
  # 输出：1.8408939659515595（均方误差）
  
  plot_model(lasso3_reg)

  

　4）分析

• α = 0.01，比岭回归中的第一个 α 的取值大很多，因为对于 RidgeRegression()，正则化的那一项中是 θ^2，平方后的结果会比较大，所以需要让 α 值很小来调节正则项的大小；而对于LassoRegression()，正则化的那一项中是 |θ|，比岭回归中的正则化项小很多，所以在 LassoRegression() 中 α 的取值可以相对大一些；

• # 在具体进行机器学习算法的过程中，需要不断的试验不断的看结果，慢慢的形成经验，用各种不同的方法在调参时，对于不同的参数大概知道参数在哪个范围内进行选择会相应的比较好；

• 当 α = 1 时，LassoRegression() 对应的正则化的程度已经比较高了；

1. 正则化的程度：拟合曲线的上下抖动幅度；

• 现实机器学习的过程中，就是在完全不进行模型正则化和过度模型正则化之间选择一个程度最好的一情况；

四、比较 Ridge Regression 和 LASSO Regression

• 

　1）使用 Ridge 改进的多项式回归算法，随着 α 的改变，拟合曲线始终是各曲线，直到最后变成一条几乎水平的直线；也就是说，使用 Ridge 改造的多项式回归算法，得到的模型变量前还是有系数，因此很难得到一天斜的直线；

　2）而使用 Lasso 改进的多项式回归算法，随着 α 的改变，拟合曲线会很快变成一条斜的直线，最后慢慢变成一条几乎水平的直线；模型更倾向于一条直线。

五、其它

•  LASSO 的特点：趋向于使得一部分 θ 值变为 0，也就是说 LASSO 认为与 θ = 0 对应的特征是完全没有用的，而剩下与 θ 不为 0 所对应的特征是有用的，所以 LASSO 可作为特征选择用；

• 在作为特征选择用时，LASSO 也可能将一些有用的特征的系数 θ 变为 0，会导致信息不准确；相比较来说，还是 Ridge 更准确。

1. 但是如果样本特征非常的大，如使用多项式回归时 degree = 100，此种情况下使用 LASSO 可以使样本特征变小；