一、基础理解
模型正则化(Regularization)
# 有多种操作方差,岭回归只是其中一种方式;
- 功能:通过限制超参数大小,解决过拟合或者模型含有的巨大的方差误差的问题;
-
影响拟合曲线的两个因子
- 模型参数 θi (1 ≤ i ≤ n):决定拟合曲线上下抖动的幅度;
- 模型截距 θ0:决定整体拟合曲线上下位置的高低;
二、岭回归
- 岭回归(Ridge Regression):模型正则化的一种方式;

- 解决的问题:模型过拟合;
- 思路:拟合曲线上下抖动的幅度主要受模型参数的影响,限制参数的大小可以限制拟合曲线抖动的幅度;
1)原理及操作
- 思路(以多项式回归为例):在原来的损失函数中加入一个含有所有变量的代数式,此时如果想让目标函数尽可能的小,也必须考虑让所有的参数 θi2 尽可能的小,进而可以降低拟合曲线上下的抖动幅度;
2)公式推导

- 加入的模型正则化:
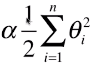 ;
;
- θi :决定拟合曲线的每一部分的抖动幅度,其中 i 取值范围 1 ~ n ,不包含 0,因为 θ0 表示模型的截距;
- θ0 :决定拟合曲线整体的上下位置的高低;
- 1/2 :方便计算,因为对式子求导后 θi2 变成 2θi ,产生的系数 2 刚好与 1/2 相乘为 1;但由于有 α 的存在,1/2 加与不加都没关系;
- α :引入的新的超参数,平衡新的损失函数中两部分的关系;是代数式的系数,代表在模型正则化下新的损失函数中,让每一个 θi 都尽可能的小,这个小的程度占整个优化损失函数程度的多少;
- 如果 α = 0:表示目标函数中没有加入模型正则化;
- 如果 α = +∞ :目标函数的另一部分 MSE 占整个目标函数的比重非常的小,主要的优化任务就是让每一个 θi 都尽可能的小;
三、实例查看岭回归对模型的影响
1)模拟数据集
-
import numpy as np import matplotlib.pyplot as plt np.random.seed(42) # np.random.uniform(-3, 3, size=100):在 [-3, 3] 之间等分取 100 个数; x = np.random.uniform(-3.0, 3.0, size=100) X = x.reshape(-1, 1) y = 0.5 * x + 3. + np.random.normal(0, 1, size=100) plt.scatter(x, y) plt.show()
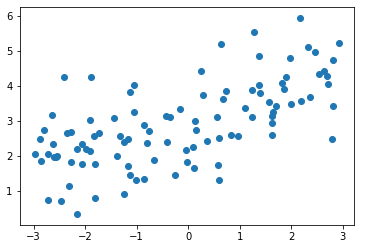
2)使用多形式回归过拟合数据
-
使用管道的方式使用多项式回归
from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LinearRegression # 使用多项式回归的管道方法 def PolynomialRegression(degree): return Pipeline([ ('poly', PolynomialFeatures(degree=degree)), ('std_scaler', StandardScaler()), ('lin_reg', LinearRegression()) ]) from sklearn.model_selection import train_test_split np.random.seed(666) X_train, X_test, y_train, y_test = train_test_split(X, y) from sklearn.metrics import mean_squared_error poly_reg = PolynomialRegression(degree=20) poly_reg.fit(X_train, y_train) y_poly_predict = poly_reg.predict(X_test) mean_squared_error(y_test, y_poly_predict) # 输出:167.9401086729357
# 均方误差:167.9401086729357
-
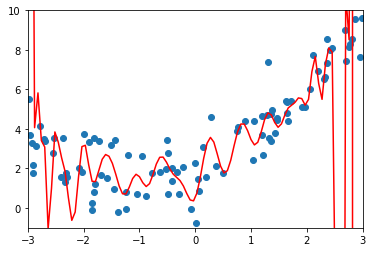
绘制模型曲线
# np.linspace(-3, 3, 100):在 [-3, 3] 之间等分取 100 个数,包含 -3 和 3; X_plot = np.linspace(-3, 3, 100).reshape(100, 1) y_plot = poly_reg.predict(X_plot) plt.scatter(x, y) plt.plot(X_plot[:, 0], poly_reg.predict(X_plot), color='r') plt.axis([-3, 3, 0, 6]) plt.show()
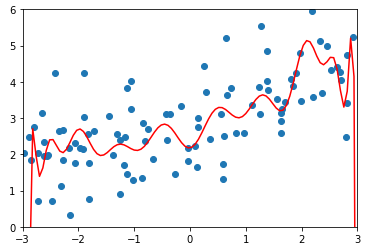
3)使用岭回归
- from sklearn.linear_model import Ridge
-
将绘图代码封装为一个函数
def plot_model(model): X_plot = np.linspace(-3, 3, 100).reshape(100, 1) y_plot = model.predict(X_plot) plt.scatter(x, y) plt.plot(X_plot[:, 0], model.predict(X_plot), color='r') plt.axis([-3, 3, 0, 6]) plt.show()
-
使用管道的方式使用岭回归方法
from sklearn.linear_model import Ridge def RidgeRegression(degree, alpha): return Pipeline([ ('poly', PolynomialFeatures(degree=degree)), ('std_scaler', StandardScaler()), ('ridge_reg', Ridge(alpha=alpha)) ])
-
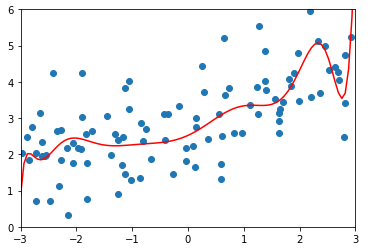
degree = 20、α = 0.0001
ridge1_reg = RidgeRegression(20, 0.0001) ridge1_reg.fit(X_train, y_train) y1_predict = ridge1_reg.predict(X_test) mean_squared_error(y_test, y1_predict) # 输出:1.323349275406402(均方误差) plot_model(ridge1_reg)
-
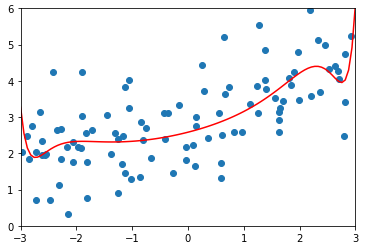
degree = 20、α = 1
ridge2_reg = RidgeRegression(20, 1) ridge2_reg.fit(X_train, y_train) y2_predict = ridge2_reg.predict(X_test) mean_squared_error(y_test, y2_predict) # 输出:1.1888759304218448(均方误差) plot_model(ridge2_reg)
-
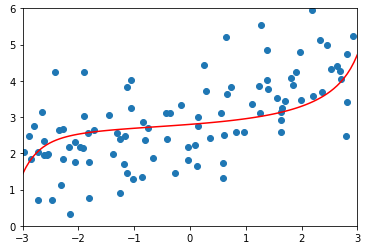
degree = 20、α = 100
ridge3_reg = RidgeRegression(20, 100) ridge3_reg.fit(X_train, y_train) y3_predict = ridge3_reg.predict(X_test) mean_squared_error(y_test, y3_predict) # 输出:1.3196456113086197(均方误差) plot_model(ridge3_reg)
-
degree=20、alpha=1000000(相当于无穷大)
ridge4_reg = RidgeRegression(20, 1000000) ridge4_reg.fit(X_train, y_train) y4_predict = ridge4_reg.predict(X_test) mean_squared_error(y_test, y4_predict) # 输出:1.8404103153255003 plot_model(ridge4_reg)

- 当 α = 1000000(相当于无穷大)时:拟合曲线几乎是一条水平的直线,因为当 α 非常大的时候,对目标函数的影响相当于只有添加的模型正则化在起作用;