CF1012B Solution

题目链接

题解

可以发现，能够使另一个方格填色的三个方格的坐标可以写为((a,b),(a,c),(c,d))，由((a,b))以(a)为检索可以找到((a,c))，而((a,c))以(c)为检索找到((c,d))。由此想到，将行、列数构造为点，而每一个方格则是一条无向边。如题目样例3可构造为如下的图：

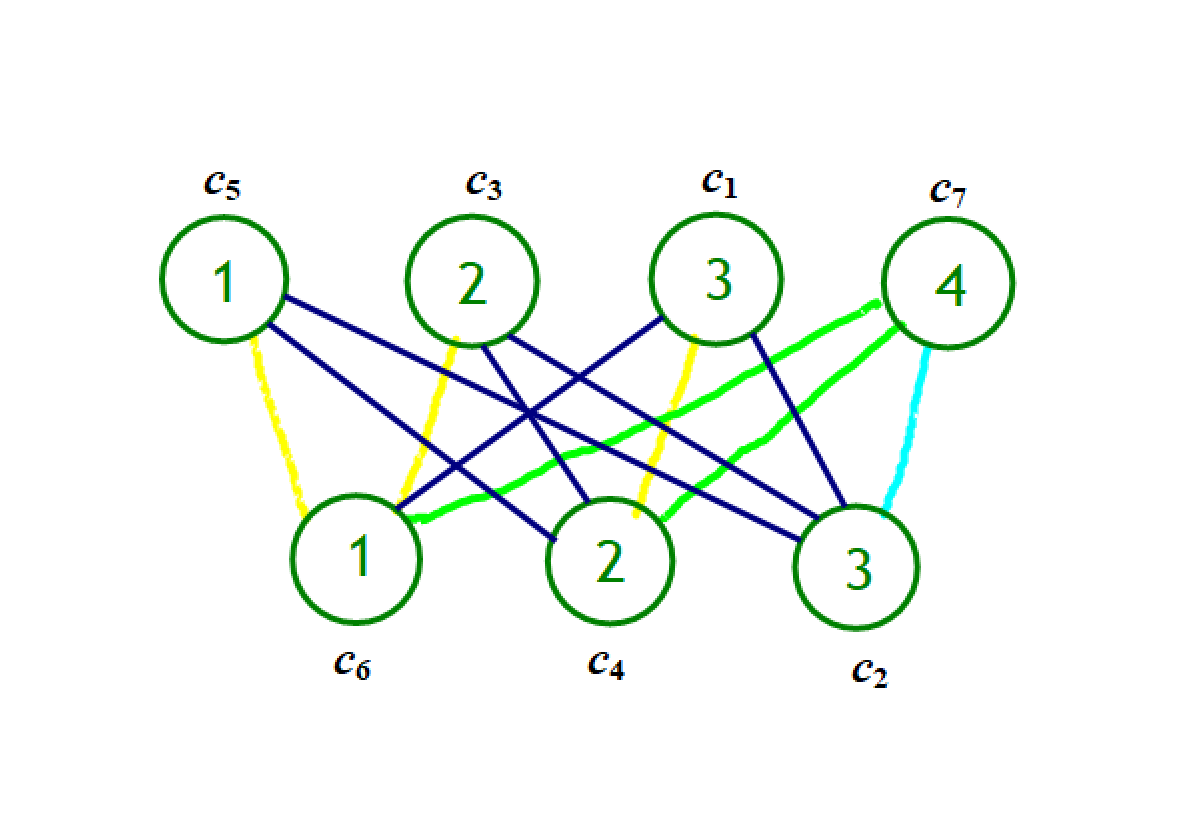
其中深蓝色的边是题目中已给出的格子。例如((C_5,C_2,C_1,C_6))四个联通的点即可推断出一条新边(C_5C_6)，图中用黄色笔画出，代表格子((1,1))可以被填充，其余黄边同理。而这时，点(C_7)仍未与其他点联通，也就是格子((4,1),(4,2),(4,3))未被填充。因此必须消耗一次填涂次数，添加一条边(C_7C_2)（(C_7C_4,C_7C_6)亦可），也就是图中浅蓝色边。而通过这条边可以推断出另2条绿边，最终该图变为完全二分图，全部填充完毕。

但是无法直接枚举点递归，因为这样时间为(O(nq))。可以发现，每一个连通图一定可以通过上述推导化为完全二分图，证明：当连通图中节点数(ge 3)时，一定可以划分为若干个由(3)个节点组成的连通子图，由其可连接新边使之称为环。而与该环连接的其他点一定可以通过推导与环中全部节点连接（过程略），因为此图为连通图，所有节点均可通过相邻节点与该子图（环）连接。所以只需使构造出的图成为连通图，即将所有连通子图连接，需建新边数(=)连通子图数(-1)。

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=4e5+10;
int fst[N],nxt[2*N],v[2*N],cnt;
bool vis[N];//vis[i]:是否(1/0)已经过编号为i的节点
void add(int x,int y)
{
	v[++cnt]=y;
	nxt[cnt]=fst[x]; fst[x]=cnt;
}
void dfs(int x)
{
	vis[x]=1;
	for(int i=fst[x];i;i=nxt[i])
	{
		int y=v[i];
		if(!vis[y]) dfs(y);
	}
}
int main()
{
	int n,m,q,ans=0;
	scanf("%d%d%d",&n,&m,&q);
	int x,y;
	for(int i=1;i<=q;i++)
	{
		scanf("%d%d",&x,&y);
		add(x,n+y); add(n+y,x);
	}
	for(int i=1;i<=n+m;i++)//统计联通子图个数
		if(!vis[i]) {dfs(i); ans++;}
	printf("%d",ans-1);
	return 0;
}