https://www.cnblogs.com/violet-acmer/p/10005351.html
•题意
有n个节目，每个节目都有个开始时间和结束时间。
定义 x,y 分别为租电视需要的花费和看电视需要的花费（应该是花的电费，哈哈）。
假如某电视节目的播放区间是[a,b]，那么看完这个节目需要的总花费为x+(b-a)*y。
如果有其他节目的播放区间是[b,c]，那么便不能和[a,b]的节目用同一个电视看。
求看完所有电视节目所需要的最少花费。
•题解
对于每个节目的播放区间[a,b]，都会有个(b-a)*y 的花费；
能省钱的地方在“节目 i 是选择和之前的某个节目 j 共用一个电视，还是选择新租一个电视”；
这个只需要寻找一下有没有某个节目 j ，使得节目 i 和 j 共用一个电视要比 i 新租一个电视省钱。
(1):按节目开始时间从小到大排序，对于相同的开始时间，谁在前谁在后都可以。
(2):排序后，从第一个节目开始开始遍历。
假设来到第 i 个节目，查找节目 j，满足节目 j 的结束时间早于节目 i 的开始时间，并且节目 j 的结束时间尽可能晚；
判断节目 i 是否可以和节目 j 共用一个电视；
•贪心策略的证明（个人理解）
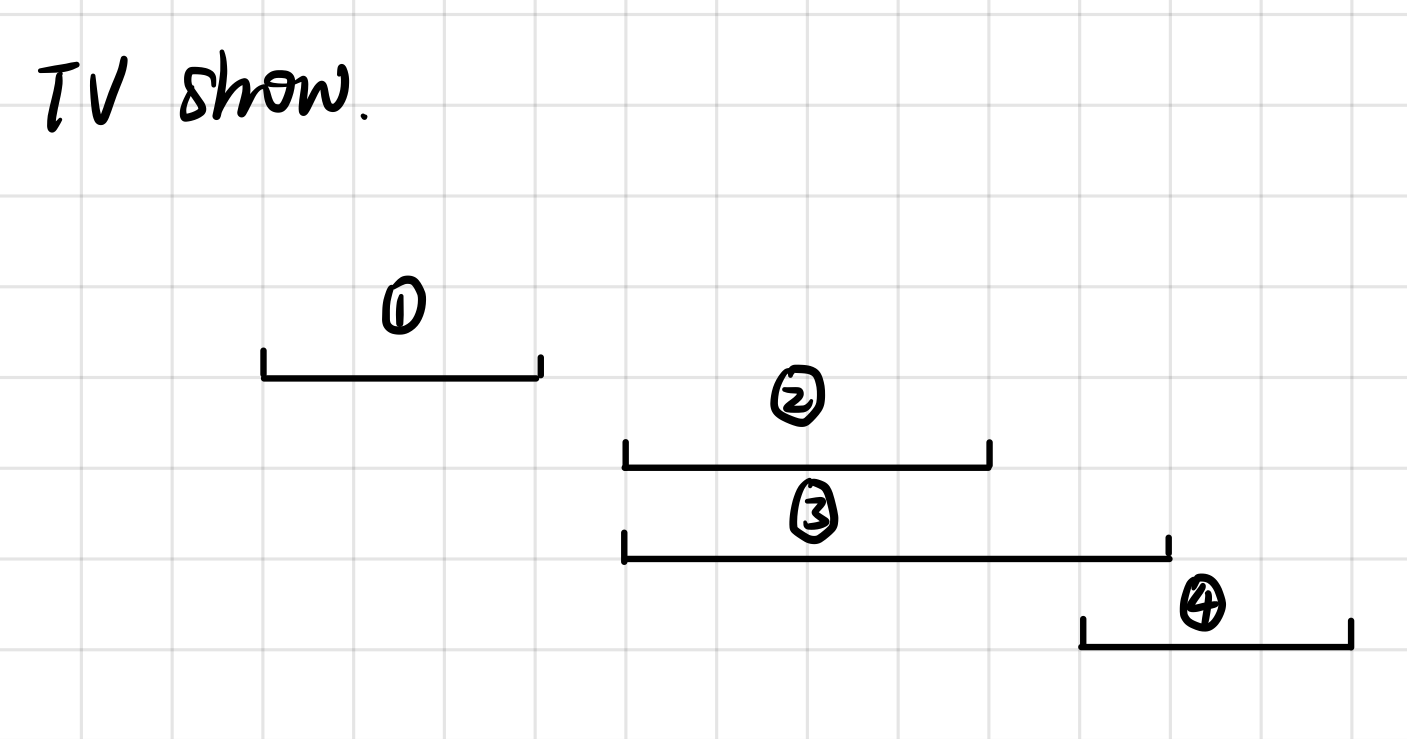
假设有①②③④节目，排好序后如下所示：
对于排序策略“相同的开始时间，谁在前谁在后都可以”的理解：
②③节目开始时间相同，假设 x > y，那么①②③节目的总花费有两种不同的策略，1.(①,②)+③ 和 2.(①,③)+②
方案1的总花费为 (x+(9-1)*y) + (x+(11-5)*y) = 2*x+14*y.
方案2的总花费为 (x+(11-1)*y) + (x+(9-5)*y) = 2*x+14*y.
显然，这两种方案所花费的价钱是相同的。
此题的难点在于“如何高效查找节目 j"；
一开始本来打算开两个数组，一个数组存储节目的开始时间，一个数组存储节目的结束时间；
并用map存储结束时间相同的总节目数，然后，遍历的时候在结束时间的数组中二分查找；
实现了一下，又仔细想了想，感觉不行，还是太菜了。。。。。
没办法了，只好求助了，翻了翻大神博客，发现，差不多都用到了multiset这个容器，然后，补了补multiset；（tql）
•Code
View Code1 #include<iostream> 2 #include<set> 3 #include<cstdio> 4 #include<algorithm> 5 using namespace std; 6 #define ll __int64 7 const int MOD=1e9+7; 8 const int maxn=1e5+10; 9 10 int n,x,y; 11 int res; 12 struct Node 13 { 14 int l,r; 15 Node(int _a=0,int _b=0):l(_a),r(_b){} 16 }show[maxn]; 17 multiset<int >_set; 18 19 bool cmp(Node _a,Node _b) 20 { 21 return _a.l < _b.l; 22 } 23 int Solve() 24 { 25 sort(show+1,show+n+1,cmp); 26 for(int i=1;i <= n;++i) 27 { 28 multiset<int >::iterator it; 29 it=_set.lower_bound(show[i].l);//二分查找 30 //it=lower_bound(_set.begin(),_set.end(),show[i].l); 31 if(it == _set.begin())//如果it == _set.begin()，说明 i 之前没有结束时间比其小的电视节目 32 { 33 res += x; 34 res %= MOD; 35 _set.insert(show[i].r); 36 } 37 else 38 { 39 it--;//当前的it指向的时间是第一个 >= show[i].l，所以，要it--才是最靠近show[i].l的结束时间 40 ll cost=1ll*(show[i].l-*it)*y; 41 if(cost <= x) 42 { 43 res += cost; 44 _set.erase(it); 45 } 46 else 47 res += x; 48 res %= MOD; 49 _set.insert(show[i].r); 50 } 51 } 52 return res%MOD; 53 } 54 int main() 55 { 56 scanf("%d%d%d",&n,&x,&y); 57 for(int i=1;i <= n;++i) 58 { 59 int l,r; 60 scanf("%d%d",&l,&r); 61 show[i]=Node(l,r); 62 res += 1ll*(r-l)*y%MOD;//记得加 1ll 防止爆int 63 res %= MOD; 64 } 65 printf("%d ",Solve()); 66 }
分割线：2019.7.2
•Code
View Code1 #include<bits/stdc++.h> 2 using namespace std; 3 #define ll long long 4 const int MOD=1e9+7; 5 const int maxn=1e5+50; 6 7 int n; 8 ll x,y; 9 struct Data 10 { 11 int l,r; 12 bool operator < (const Data &obj) const 13 { 14 return l < obj.l; 15 } 16 }tv[maxn]; 17 multiset<int >_set; 18 multiset<int >::iterator it; 19 20 ll Solve() 21 { 22 sort(tv+1,tv+n+1); 23 24 ll ans=0; 25 for(int i=1;i <= n;++i)///求出每个节目都需要一台电视的总花费 26 ans=(ans+x+(tv[i].r-tv[i].l)*y)%MOD; 27 28 _set.clear(); 29 for(int i=1;i <= n;++i) 30 { 31 it=_set.lower_bound(tv[i].l); 32 if(it != _set.begin()) 33 { 34 --it; 35 ll cur=(tv[i].l-*it)*y; 36 if(cur <= x)///如果可以共用一台电视 37 { 38 ans=(ans+cur-x+MOD)%MOD; 39 _set.erase(it); 40 } 41 } 42 _set.insert(tv[i].r); 43 } 44 return ans%MOD; 45 } 46 int main() 47 { 48 // freopen("C:\Users\hyacinthLJP\Desktop\in&&out\contest","r",stdin); 49 scanf("%d%lld%lld",&n,&x,&y); 50 for(int i=1;i <= n;++i) 51 { 52 int l,r; 53 scanf("%d%d",&l,&r); 54 tv[i]=Data{l,r}; 55 } 56 printf("%lld ",Solve()); 57 58 return 0; 59 }