数据结构丨数组和字符串

数组简介

数组简介

数组是一种基本的数据结构，用于按顺序存储元素的集合。但是元素可以随机存取，因为数组中的每个元素都可以通过数组索引来识别。

数组可以有一个或多个维度。这里我们从一维数组开始，它也被称为线性数组。这里有一个例子：

在上面的例子中，数组 A 中有 6 个元素。也就是说，A 的长度是 6 。我们可以使用 A[0] 来表示数组中的第一个元素。因此，A[0] = 6 。类似地，A[1] = 3，A[2] = 8，依此类推。

数组中的操作

让我们来看看数组的用法：

#include <iostream>

int main() {
    // 1. Initialize
    int a0[5];
    int a1[5] = {1, 2, 3};  // other element will be set as the default value
    // 2. Get Length
    int size = sizeof(a1) / sizeof(*a1);
    cout << "The size of a1 is: " << size << endl;
    // 3. Access Element
    cout << "The first element is: " << a1[0] << endl;
    // 4. Iterate all Elements
    cout << "[Version 1] The contents of a1 are:";
    for (int i = 0; i < size; ++i) {
        cout << " " << a1[i];
    }
    cout << endl;
    cout << "[Version 2] The contents of a1 are:";
    for (int& item: a1) {
        cout << " " << item;
    }
    cout << endl;
    // 5. Modify Element
    a1[0] = 4;
    // 6. Sort
    sort(a1, a1 + size);
}

动态数组

正如我们在上一篇文章中提到的，数组具有固定的容量，我们需要在初始化时指定数组的大小。有时它会非常不方便并可能造成浪费。

因此，大多数编程语言都提供内置的动态数组，它仍然是一个随机存取的列表数据结构，但大小是可变的。例如，在 C++ 中的 vector，以及在 Java 中的 ArrayList。

动态数组中的操作

让我们来看看动态数组的用法：

#include <iostream>

int main() {
    // 1. initialize
    vector<int> v0;
    vector<int> v1(5, 0);
    // 2. make a copy
    vector<int> v2(v1.begin(), v1.end());
    vector<int> v3(v2);
    // 2. cast an array to a vector
    int a[5] = {0, 1, 2, 3, 4};
    vector<int> v4(a, *(&a + 1));
    // 3. get length
    cout << "The size of v4 is: " << v4.size() << endl;
    // 4. access element
    cout << "The first element in v4 is: " << v4[0] << endl;
    // 5. iterate the vector
    cout << "[Version 1] The contents of v4 are:";
    for (int i = 0; i < v4.size(); ++i) {
        cout << " " << v4[i];
    }
    cout << endl;
    cout << "[Version 2] The contents of v4 are:";
    for (int& item : v4) {
        cout << " " << item;
    }
    cout << endl;
    cout << "[Version 3] The contents of v4 are:";
    for (auto item = v4.begin(); item != v4.end(); ++item) {
        cout << " " << *item;
    }
    cout << endl;
    // 6. modify element
    v4[0] = 5;
    // 7. sort
    sort(v4.begin(), v4.end());
    // 8. add new element at the end of the vector
    v4.push_back(-1);
    // 9. delete the last element
    v4.pop_back();
}

寻找数组的中心索引

给定一个整数类型的数组 nums，请编写一个能够返回数组“中心索引”的方法。

我们是这样定义数组中心索引的：数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。

如果数组不存在中心索引，那么我们应该返回 -1。如果数组有多个中心索引，那么我们应该返回最靠近左边的那一个。

示例 1:

输入: 
nums = [1, 7, 3, 6, 5, 6]
输出: 3
解释: 
索引3 (nums[3] = 6) 的左侧数之和(1 + 7 + 3 = 11)，与右侧数之和(5 + 6 = 11)相等。
同时, 3 也是第一个符合要求的中心索引。

示例 2:

输入: 
nums = [1, 2, 3]
输出: -1
解释: 
数组中不存在满足此条件的中心索引。

说明:

• nums 的长度范围为 [0, 10000]。
• 任何一个 nums[i] 将会是一个范围在 [-1000, 1000]的整数。

class Solution{
public:
    int pivotIndex(vector<int>& nums){
        if(nums.size() == 0)
            return -1;
        int sum = accumulate(nums.begin(), nums.end(), 0);

        int leftSum = 0;
        for(int i=0; i<nums.size(); i++)
            if(leftSum == sum-leftSum-nums[i])
                return i;
            else 
                leftSum += nums[i];
        
        return -1;
    }
};

至少是其他数字两倍的最大数

在一个给定的数组nums中，总是存在一个最大元素 。

查找数组中的最大元素是否至少是数组中每个其他数字的两倍。

如果是，则返回最大元素的索引，否则返回-1。

示例 1:

输入: nums = [3, 6, 1, 0]
输出: 1
解释: 6是最大的整数, 对于数组中的其他整数,
6大于数组中其他元素的两倍。6的索引是1, 所以我们返回1.

示例 2:

输入: nums = [1, 2, 3, 4]
输出: -1
解释: 4没有超过3的两倍大, 所以我们返回 -1.

提示:

1. nums 的长度范围在[1, 50].
2. 每个 nums[i] 的整数范围在 [0, 99].

#include <iostream>
#include <vector>

using namespace std;

/// Linear Scan
/// Time Complexity: O(n)
/// Space Complexity: O(1)
class Solution{
public:
    int dominantIndex(vector<int>& nums){
        int maxNum = *max_element(nums.begin(), nums.end());
        int res = -1;
        for(int i = 0; i< nums.size(); i++)
            if(nums[i] != maxNum){
                if(maxNum < 2*nums[i])
                    return -1;
            }
            else
                res = i;
        return res;
    }
};

加一

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储一个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例 1:

输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。

示例 2:

输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。

#include <iostream>
#include <vector>

using namespace std;

/// Ad Hoc
/// Time Complexity: O(n)
/// Space Complexity: O(1)
class Solution{
public:
    vector<int> plusOne(vector<int>& digits){
        digits[digits.size() -1] ++;
        for(int i=digits.size()-1; i>=1; i--)
            if(digits[i] == 10){
                digits[i] = 0;
                digits[i-1] ++;
            }
        if(digits[0] == 10){
            digits[0] = 0;
            digits.insert(digits.begin(), 1);
        }
        return digits;
    }
}

二维数组简介

二维数组简介

类似于一维数组，二维数组也是由元素的序列组成。但是这些元素可以排列在矩形网格中而不是直线上。

示例

#include <iostream>

template <size_t n, size_t m>
void printArray(int (&a)[n][m]) {
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            cout << a[i][j] << " ";
        }
        cout << endl;
    }
}

int main() {
    cout << "Example I:" << endl;
    int a[2][5];
    printArray(a);
    cout << "Example II:" << endl;
    int b[2][5] = {{1, 2, 3}};
    printArray(b);
    cout << "Example III:"<< endl;
    int c[][5] = {1, 2, 3, 4, 5, 6, 7};
    printArray(c);
    cout << "Example IV:" << endl;
    int d[][5] = {{1, 2, 3, 4}, {5, 6}, {7}};
    printArray(d);
}

原理

在一些语言中，多维数组实际上是在内部作为一维数组实现的，而在其他一些语言中，实际上根本没有多维数组。

1. C++ 将二维数组存储为一维数组。

下图显示了大小为 M * N 的数组 A 的实际结构：

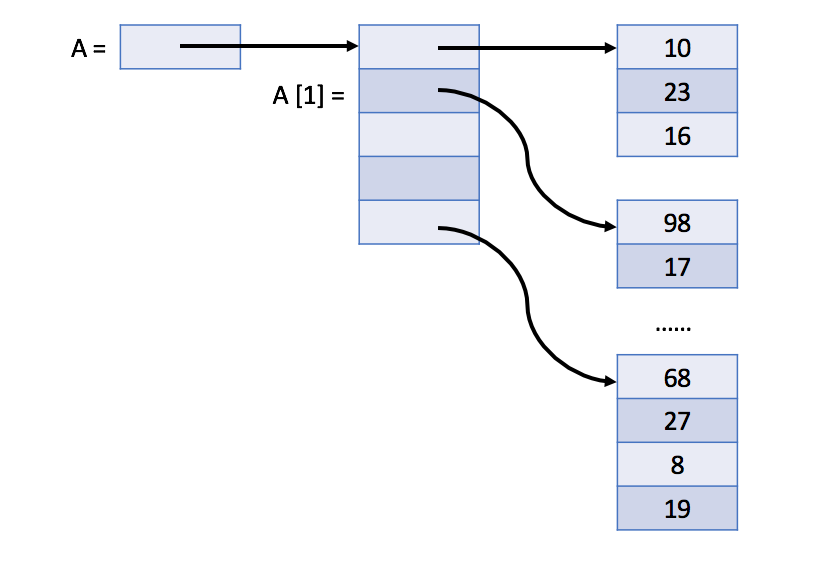
2. 在Java中，二维数组实际上是包含着 M 个元素的一维数组，每个元素都是包含有 N 个整数的数组。

下图显示了 Java 中二维数组 A 的实际结构：

动态二维数组

与一维动态数组类似，我们也可以定义动态二维数组。 实际上，它可以只是一个嵌套的动态数组。 你可以自己尝试一下。

对角线遍历

给定一个含有 M x N 个元素的矩阵（M 行，N 列），请以对角线遍历的顺序返回这个矩阵中的所有元素，对角线遍历如下图所示。

示例:

输入:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]

输出:  [1,2,4,7,5,3,6,8,9]

解释：

说明：

1. 给定矩阵中的元素总数不会超过 100000 。

#include <iostream>
#include <vector>

using namespace std;

/// Simulation
/// Time Complexity: O(n * m)
/// Space Complexity: O(1)
class Solution
{
private:
    int n, m;

public:
    vector<int> findDiagonalOrder(vector<vector<int>> &matrix)
    {
        vector<int> res;

        n = matrix.size();
        if (n == 0)
            return res;
        m = matrix[0].size();

        int x = 0, y = 0;
        int nextX, nextY;
        bool up = true;
        while (true)
        {
            res.push_back(matrix[x][y]);

            if (up)
                nextX = x - 1, nextY = y + 1;
            else
                nextX = x + 1, nextY = y - 1;
            
            if(inArea(nextX, nextY))
                x = nextX, y = nextY;
            else if(up){
                if(inArea(x, y+1))
                    y++;
                else
                    x++;
                up = false;
            }
            else{
                if(inArea(x+1, y))
                    x++;
                else
                    y++;
                up = true;
            }
            if(!inArea(x, y))
                break;
        }
        return res;
    }
private:
    bool inArea(int x, int y){
        return x>=0 && x<n && y >=0 && y<m;
    }
};

void print_vec(const vector<int>& vec){
    for(int e: vec)
        cout << e << " ";
    cout << endl;
}

int main(){
    vector<vector<int>> matrix = {
        {1, 2, 3},
        {4, 5, 6},
        {7, 8, 9}};
    
    print_vec(Solution().findDiagonalOrder(matrix));

    return 0;
}

螺旋矩阵

给定一个包含 m x n 个元素的矩阵（m 行, n 列），请按照顺时针螺旋顺序，返回矩阵中的所有元素。

示例 1:

输入:
[
 [ 1, 2, 3 ],
 [ 4, 5, 6 ],
 [ 7, 8, 9 ]
]
输出: [1,2,3,6,9,8,7,4,5]

示例 2:

输入:
[
  [1, 2, 3, 4],
  [5, 6, 7, 8],
  [9,10,11,12]
]
输出: [1,2,3,4,8,12,11,10,9,5,6,7]

/// Source : https://leetcode.com/problems/spiral-matrix/description/
/// Author : liuyubobobo
/// Time   : 2018-04-24

#include <iostream>
#include <vector>

using namespace std;


/// Simulation
/// Time Complexity: O(n^2)
/// Space Complexity: O(n^2)
class Solution {

private:
    int d[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
    int N, M;

public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {

        N = matrix.size();
        if(N == 0)
            return {};

        M = matrix[0].size();
        if(M == 0)
            return {};

        vector<vector<bool>> visited(N, vector<bool>(M, false));
        int curd = 0, curx = 0, cury = 0;
        vector<int> res;
        while(res.size() < N * M){

            if(!visited[curx][cury]) {
                res.push_back(matrix[curx][cury]);
                visited[curx][cury] = true;
            }

            int nextx = curx + d[curd][0];
            int nexty = cury + d[curd][1];
            if(inArea(nextx, nexty) && !visited[nextx][nexty]){
                curx = nextx;
                cury = nexty;
            }
            else
                curd = (curd + 1) % 4;
        }
        return res;
    }

private:
    bool inArea(int x, int y){
        return x >= 0 && x < N && y >= 0 && y < M;
    }
};


void print_vec(const vector<int>& vec){
    for(int e: vec)
        cout << e << " ";
    cout << endl;
}

int main() {

    vector<vector<int>> matrix1 = {
            {1, 2, 3},
            {4, 5, 6},
            {7, 8, 9}
    };
    print_vec(Solution().spiralOrder(matrix1));

    return 0;
}

杨辉三角

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

#include <iostream>
#include <vector>

using namespace std;

/// Simulation (Dynamic Programming)
/// Time Complexity: O(n^2)
/// Space Complexity: O(1)
class Solution{
public:
    vector<vector<int>> generate(int numRows){
        vector<vector<int>> res;
        if(numRows <= 0)
            return res;
        res.push_back({1});
        for(int i=1; i<numRows; i++){
            vector<int> row;
            row.push_back(1);
            for(int j=1; j<i; j++)
                row.push_back(res[i-1][j-1]+res[i-1][j]);
            row.push_back(1);
            res.push_back(row);
        }
        return res;
    }
};

字符串简介

字符串简介

字符串实际上是一个 unicode 字符数组。你可以执行几乎所有我们在数组中使用的操作，自己试试看吧。

然而，二者之间还是存在一些区别。在这篇文章中，我们将介绍一些在处理字符串时应该注意的问题。这些特性在不同的语言之间可能有很大不同。

比较函数

字符串有它自己的比较函数（我们将在下面的代码中向你展示比较函数的用法）。

然而，存在这样一个问题：

我们可以用 “==” 来比较两个字符串吗？

这取决于下面这个问题的答案：

我们使用的语言是否支持运算符重载？

1. 如果答案是 yes （例如 C++）。我们可以使用 “==” 来比较两个字符串。
2. 如果答案是 no （例如 Java），我们可能无法使用 “” 来比较两个字符串。当我们使用 “” 时，它实际上会比较这两个对象是否是同一个对象。

让我们运行下面的例子并比较结果：

#include <iostream>

int main() {
    string s1 = "Hello World";
    cout << "s1 is "Hello World"" << endl;
    string s2 = s1;
    cout << "s2 is initialized by s1" << endl;
    string s3(s1);
    cout << "s3 is initialized by s1" << endl;
    // compare by '=='
    cout << "Compared by '==':" << endl;
    cout << "s1 and "Hello World": " << (s1 == "Hello World") << endl;
    cout << "s1 and s2: " << (s1 == s2) << endl;
    cout << "s1 and s3: " << (s1 == s3) << endl;
    // compare by 'compare'
    cout << "Compared by 'compare':" << endl;
    cout << "s1 and "Hello World": " << !s1.compare("Hello World") << endl;
    cout << "s1 and s2: " << !s1.compare(s2) << endl;
    cout << "s1 and s3: " << !s1.compare(s3) << endl;
}

是否可变

不可变意味着一旦字符串被初始化，你就无法改变它的内容。

1. 在某些语言（如 C ++）中，字符串是可变的。 也就是说，你可以像在数组中那样修改字符串。
2. 在其他一些语言（如 Java）中，字符串是不可变的。 此特性将带来一些问题。 我们将在下一篇文章中阐明问题和解决方案。

你可以通过测试修改操作来确定你喜欢的语言中的字符串是否可变。这里有一个示例：

#include <iostream>

int main() {
    string s1 = "Hello World";
    s1[5] = ',';
    cout << s1 << endl;
}

额外操作

与数组相比，我们可以对字符串执行一些额外的操作。这里有一些例子：

#include <iostream>

int main() {
    string s1 = "Hello World";
    // 1. concatenate
    s1 += "!";
    cout << s1 << endl;
    // 2. find
    cout << "The position of first 'o' is: " << s1.find('o') << endl;
    cout << "The position of last 'o' is: " << s1.rfind('o') << endl;
    // 3. get substr
    cout << s1.substr(6, 5) << endl;
}

你应该了解这些内置操作的时间复杂度。

例如，如果字符串的长度是 N，那么查找操作和子字符串操作的时间复杂度是 O(N)。

此外，在字符串不可变的语言中，你应该额外小心连接操作（我们将在下一篇文章中解释这一点）。

在计算解决方案的时间复杂度时，不要忘记考虑内置操作的时间复杂度。

不可变字符串 —— 问题和解决方案

在上一篇文章中，您应该已经知道您喜欢的语言中的字符串是否为不可变的。如果字符串是不可变的，则会带来一些问题。希望我们也能在最后提供解决方案。

修改操作

显然，不可变字符串无法被修改。哪怕你只是想修改其中的一个字符，也必须创建一个新的字符串。

小心Java中的字符串

你应该非常小心字符串连接。让我们来看一个在 for 循环中重复进行字符串连接的例子：

#include <iostream>

int main() {
    string s = "";
    int n = 10000;
    for (int i = 0; i < n; i++) {
        s += "hello";
    }
}

请注意对于 Java 来说字符串连接有多慢？ 另一方面，在 C++ 中没有明显的性能影响。

在 Java 中，由于字符串是不可变的，因此在连接时首先为新字符串分配足够的空间，复制旧字符串中的内容并附加到新字符串。

因此，总时间复杂度将是：

5 + 5 × 2 + 5 × 3 + … + 5 × n
= 5 × (1 + 2 + 3 + … + n)
= 5 × n × (n + 1) / 2,

也就是 O(n2)。

解决方案

如果你希望你的字符串是可变的，这里有一些替代方案：

1. 如果你确实希望你的字符串是可变的，则可以将其转换为字符数组。

// "static void main" must be defined in a public class.
public class Main {
    public static void main(String[] args) {
        String s = "Hello World";
        char[] str = s.toCharArray();
        str[5] = ',';
        System.out.println(str);
    }
}

2. 如果你经常必须连接字符串，最好使用一些其他的数据结构，如 StringBuilder 。 以下代码以 O(n) 的复杂度运行。

// "static void main" must be defined in a public class.
public class Main {
    public static void main(String[] args) {
        int n = 10000;
        StringBuilder str = new StringBuilder();
        for (int i = 0; i < n; i++) {
            str.append("hello");
        }
        String s = str.toString();
    }
}

二进制求和

给定两个二进制字符串，返回他们的和（用二进制表示）。

输入为非空字符串且只包含数字 1 和 0。

示例 1:

输入: a = "11", b = "1"
输出: "100"

示例 2:

输入: a = "1010", b = "1011"
输出: "10101"

/// Source : https://leetcode.com/problems/add-binary/description/
/// Author : liuyubobobo
/// Time   : 2018-06-03

#include <iostream>

using namespace std;

/// Simulation
/// Time Complexity: O(max(len(a), len(b)))
/// Space Complexity: O(1)
class Solution {
public:
    string addBinary(string a, string b) {

        string res = a.size() > b.size() ? a : b;
        string adder = a.size() > b.size() ? b : a;

        int index = res.size() - 1;
        for(int i = adder.size() - 1 ; i >= 0 ; i --){
            res[index] += adder[i] - '0';
            index --;
        }

        for(int i = res.size() - 1 ; i > 0 ; i --)
            if(res[i] > '1'){
                res[i - 1] += 1;
                res[i] = '0' + (res[i] - '0') % 2;
            }

        if(res[0] > '1'){
            res[0] = '0' + (res[0] - '0') % 2;
            res = '1' + res;
        }
        return res;
    }
};


int main() {

    cout << Solution().addBinary("11", "1") << endl;
    cout << Solution().addBinary("1010", "1011") << endl;

    return 0;
}

实现strStr()

实现 strStr() 函数。

给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

示例 1:

输入: haystack = "hello", needle = "ll"
输出: 2

示例 2:

输入: haystack = "aaaaa", needle = "bba"
输出: -1

说明:

当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。

对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。

#include <iostream>

using namespace std;

class Solution
{
public:
    int strStr(string haystack, string needle)
    {
        if (needle.size() > haystack.size())
            return -1;
        for(int i = 0 ; i <= haystack.size() - needle.size() ; i ++){
            int j = 0;
            for(j = 0 ; j < needle.size() ; j ++)
                if(needle[j] != haystack[j + i])
                    break;
            if(j == needle.size())
                return i;
        }
        return -1;
}
};

int main() {

    cout << Solution().strStr("hello", "ll") << endl;
    cout << Solution().strStr("aaaaa", "bba") << endl;

    return 0;
}

最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1:

输入: ["flower","flow","flight"]
输出: "fl"

示例 2:

输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。

说明:

所有输入只包含小写字母 a-z 。

#include <iostream>

using namespace std;

/// Vertical Scan
/// Time Complexity: O(len(strs) * max len of string)
/// Space Complexity: O(1)
class Solution{
public: 
    string longestCommonPrefix(vector<string>& strs){
        string res = "";
        if(strs.size()==0)
            return res;
        
        for(int i=0; i<strs[0].size(); i++){
            char c = strs[0][[i];
            for(int j=1; j<strs.size(); j++)
                if(i >= strs[j].size() || strs[j][i] != c)
                    return res;
            res += c;
        }
        return res;
    }
};

int main() {

    vector<string> strs1 = {"flower","flow","flight"};
    cout << Solution().longestCommonPrefix(strs1) << endl;

    vector<string> strs2 = {"dog","racecar","car"};
    cout << Solution().longestCommonPrefix(strs2) << endl;

    return 0;
}

双指针技巧

双指针技巧 —— 情景一

在前一章中，我们通过迭代数组来解决一些问题。通常，我们只使用从第一个元素开始并在最后一个元素结束的一个指针来进行迭代。 但是，有时候，我们可能需要同时使用两个指针来进行迭代。

示例

让我们从一个经典问题开始：

反转数组中的元素。

其思想是将第一个元素与末尾进行交换，再向前移动到下一个元素，并不断地交换，直到它到达中间位置。

我们可以同时使用两个指针来完成迭代：一个从第一个元素开始，另一个从最后一个元素开始。持续交换它们所指向的元素，直到这两个指针相遇。

以下代码可以供你参考：

void reverse(int *v, int N) {
    int i = 0;
    int j = N - 1;
    while (i < j) {
        swap(v[i], v[j]);
        i++;
        j--;
    }
}

总结

总之，使用双指针技巧的典型场景之一是你想要

从两端向中间迭代数组。

这时你可以使用双指针技巧：

一个指针从始端开始，而另一个指针从末端开始。

值得注意的是，这种技巧经常在排序数组中使用。

反转字符串

编写一个函数，其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。

不要给另外的数组分配额外的空间，你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。

你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。

示例 1：

输入：["h","e","l","l","o"]
输出：["o","l","l","e","h"]

示例 2：

输入：["H","a","n","n","a","h"]
输出：["h","a","n","n","a","H"]

#include <iostream>
#include <vector>
using namespace std;

/// Two Pointers
/// Time Complexity: O(n)
/// Space Complexity: O(1)
class Solution{
public: 
    void reverseString(vector<char>& s){
        int i=0, j=s.size()-1;
        while(i<j){
            swap(s[i], s[j]);
            i ++;
            j --;
        }
    }
};

数组拆分I

给定长度为 2n 的数组, 你的任务是将这些数分成 n 对, 例如 (a1, b1), (a2, b2), ..., (an, bn) ，使得从1 到 n 的 min(ai, bi) 总和最大。

示例 1:

输入: [1,4,3,2]

输出: 4
解释: n 等于 2, 最大总和为 4 = min(1, 2) + min(3, 4).

提示:

1. n 是正整数,范围在 [1, 10000].
2. 数组中的元素范围在 [-10000, 10000].

#include <iostream>
#include <vector>

using namespace std;

/// Sort
/// Time Complexity: O(nlogn)
/// Space Complexity: O(1)
class Solution {
public:
    int arrayPairSum(vector<int>& nums){
        sort(nums.begin(), nums.end());
        int sum = 0;
        for(int i=0; i<nums.size(); i+=2)
            sum+=nums[i];
        return sum;
    }
};

两数之和 II - 输入有序数组

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:

• 返回的下标值（index1 和 index2）不是从零开始的。
• 你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例:

输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

#include <iostream>
#include <vector>
#include <cassert>

using namespace std;

// Two Pointers
// Time Complexity: O(n)
// Space Complexity: O(1)
class Solution {

public:
    vector<int> twoSum(vector<int>& numbers, int target) {

        assert(numbers.size() >= 2);
        // assert(isSorted(numbers));

        int l = 0, r = numbers.size() - 1;
        while(l < r){

            if(numbers[l] + numbers[r] == target){
                int res[2] = {l+1, r+1};
                return vector<int>(res, res+2);
            }
            else if(numbers[l] + numbers[r] < target)
                l ++;
            else // numbers[l] + numbers[r] > target
                r --;
        }

        throw invalid_argument("the input has no solution");
    }

private:
    bool isSorted(const vector<int>& numbers){
        for(int i = 1 ; i < numbers.size() ; i ++)
            if(numbers[i] < numbers[i-1])
                return false;
        return true;
    }

};

void printVec(const vector<int>& vec){
    for(int e: vec)
        cout << e << " ";
    cout << endl;
}

int main() {

    int nums[] = {2, 7, 11, 15};
    vector<int> vec(nums, nums + sizeof(nums) / sizeof(int));
    int target = 9;
    printVec(Solution().twoSum(vec, target));

    return 0;
}

双指针技巧 —— 情景二

有时，我们可以使用两个不同步的指针来解决问题。

示例

让我们从另一个经典问题开始：

给定一个数组和一个值，原地删除该值的所有实例并返回新的长度。

如果我们没有空间复杂度上的限制，那就更容易了。我们可以初始化一个新的数组来存储答案。如果元素不等于给定的目标值，则迭代原始数组并将元素添加到新的数组中。

实际上，它相当于使用了两个指针，一个用于原始数组的迭代，另一个总是指向新数组的最后一个位置。

重新考虑空间限制

现在让我们重新考虑空间受到限制的情况。

我们可以采用类似的策略，我们继续使用两个指针：一个仍然用于迭代，而第二个指针总是指向下一次添加的位置。

以下代码可以供你参考：

int removeElement(vector<int>& nums, int val) {
    int k = 0;
    for (int i = 0; i < nums.size(); ++i) {
        if (nums[i] != val) {
            nums[k] = nums[i];
            ++k;
        }
    }
    return k;
}

在上面的例子中，我们使用两个指针，一个快指针 i 和一个慢指针 k 。i 每次移动一步，而 k 只在添加新的被需要的值时才移动一步。

总结

这是你需要使用双指针技巧的一种非常常见的情况：

同时有一个慢指针和一个快指针。

解决这类问题的关键是

确定两个指针的移动策略。

与前一个场景类似，你有时可能需要在使用双指针技巧之前对数组进行排序，也可能需要运用贪心想法来决定你的运动策略。

移除元素

给定一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

示例 1:

给定 nums = [3,2,2,3], val = 3,

函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。

你不需要考虑数组中超出新长度后面的元素。

示例 2:

给定 nums = [0,1,2,2,3,0,4,2], val = 2,

函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。

注意这五个元素可为任意顺序。

你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以“引用”方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

#include <iostream>
#include <vector>
#include <cassert>
#include <stdexcept>

using namespace std;


/// Two Pointers
///Time Complexity: O(n)
/// Space Complexity: O(1)
class Solution {

public:
    int removeElement(vector<int>& nums, int val) {

        int newl = 0;
        for( int i = 0 ; i < nums.size() ; i ++ )
            if( nums[i] != val )
                nums[newl++] = nums[i];

        return newl;
    }
};


int main() {

    vector<int> nums = {3, 2, 2, 3};
    int val = 3;

    cout << Solution().removeElement(nums, val) << endl;

    return 0;
}

最大连续1的个数

给定一个二进制数组， 计算其中最大连续1的个数。

示例 1:

输入: [1,1,0,1,1,1]
输出: 3
解释: 开头的两位和最后的三位都是连续1，所以最大连续1的个数是 3.

注意：

• 输入的数组只包含 0 和1。
• 输入数组的长度是正整数，且不超过 10,000。

#include <iostream>
#include <vector>

using namespace std;

/// Ad-Hoc
/// Time Complexity: O(n)
/// Space Complexity: O(1)
class Solution{
public: 
    int findMaxConsecutiveOnes(vector<int>& nums){
        int res = 0;
        int start = firstOne(nums, 0);
        for(int i=start+1; i<= nums.size(); ){
            if(i == nums.size() || nums[i] != 1){
                res = max(res, i-start);
                start = firstOne(nums, i);
                i = start + 1;
            }
            else 
                i++;
        }
        return res;
    }
private: 
    int firstOne(const vector<int>& nums, int startIndex){
        for(int i=startIndex; i<nums.size(); i++)
            if(nums[i]==1)
                return i;
        return nums.size();
    }
};

int main() {

    vector<int> nums = {1, 1, 0, 1, 1, 1};
    cout << Solution().findMaxConsecutiveOnes(nums) << endl;
    return 0;
}

长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组，返回 0。

示例:

输入: s = 7, nums = [2,3,1,2,4,3]
输出: 2
解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。

进阶:

如果你已经完成了O(n) 时间复杂度的解法, 请尝试 O(n log n) 时间复杂度的解法。

#include <iostream>
#include <cassert>
#include <vector>
#include <algorithm>

using namespace std;

class Solution{
public: 
    int minSubArrayLen(int s, vector<int>& nums){
        if (nums.size() == 0) return 0;
        int i=0, j=0, sum=0, min=INT_MAX;
        while(j<nums.size()){
            sum += nums[j++];
            while(sum >= s){
                min = (min < j-i)? min : (j-i);
                sum -= nums[i++];
            }
        }
        return min == INT_MAX? 0:min;
    }
};

小结

数组相关的技术

你可能想要了解更多与数组相关的数据结构或技术。我们不会深入研究这张卡片中的大多数概念，而是在本文中提供相应卡片的链接。

1. 这里有一些其他类似于数组的数据结构，但具有一些不同的属性：

• 字符串（已包含在本卡片中）
• 哈希表
• 链表
• 队列
• 栈

2. 正如我们所提到的，我们可以调用内置函数来对数组进行排序。但是，理解一些广泛使用的排序算法的原理及其复杂度是很有用的。

3. 二分查找也是一种重要的技术，用于在排序数组中搜索特定的元素。

4. 我们在这一章中引入了双指针技巧。想要灵活运用该技技巧是不容易的。这一技巧也可以用来解决：

• 链表中的慢指针和快指针问题
• 滑动窗口问题

5. 双指针技巧有时与贪心算法有关，它可以帮助我们设计指针的移动策略。 在不久的将来，我们会提供更多的卡片来介绍上面提到的这些技术，并更新链接。

旋转数组

给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。

示例 1:

输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释: 
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]

说明:

• 尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
• 要求使用空间复杂度为 O(1) 的原地算法。

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

/// Using Queue
/// Time Complexity: O(n^2)
/// Space Complexity: O(n)
class SolutionA {
public:
    void rotate(vector<int>& nums, int k) {

        queue<int> q;
        while(k -- && !nums.empty())
            q.push(nums.back()), nums.pop_back();
        for(int i = 0 ; i <= k ; i ++)  //if k >= nums.size()
            q.push(q.front()), q.pop();

        while(!q.empty())
            nums.insert(nums.begin(), q.front()), q.pop();
        return;
    }
};

/// Cyclic Replacements
/// Time Complexity: O(n)
/// Space Complexity: O(1)
class SolutonB{
public: 
    void rotate(vector<int>& nums, int k){
        int start = 0, cur = 0, t = nums[cur];
        for(int i=0; i<nums.size(); i++){
            int next = (cur + k) % nums.size();
            int t2 = nums[next];
            nums[next] = t;
            t = t2;
            cur = next;

            if(cur == start)
                start++, cur=start, t=nums[cur];
        }
    }
};

/// Using Reverse
/// Time Complexity: O(n)
/// Space Complexity: O(1)
class SolutionC {
public:
    void rotate(vector<int>& nums, int k) {

        k %= nums.size();
        reverse(nums, 0, nums.size() - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, nums.size() - 1);
    }

private:
    void reverse(vector<int>& nums, int start, int end){
        for(int i = start, j = end; i < j; i ++, j --)
            swap(nums[i], nums[j]);
    }
};

void print_vec(const vector<int>& vec){
    for(int e: vec)
        cout << e << " ";
    cout << endl;
}

int main() {

    vector<int> nums1 = {1, 2, 3, 4, 5, 6, 7};
    SolutionC().rotate(nums1, 3);
    print_vec(nums1);

    vector<int> nums2 = {1, 2};
    SolutionC().rotate(nums2, 3);
    print_vec(nums2);

    return 0;
}

杨辉三角 II

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

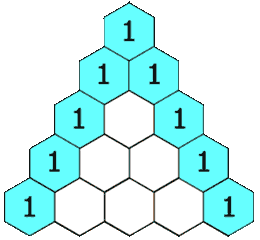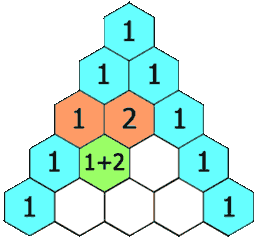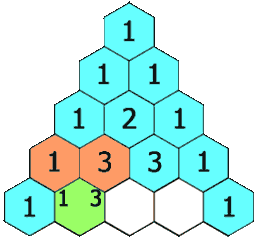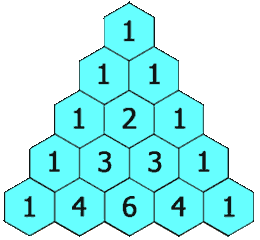
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例:

输入: 3
输出: [1,3,3,1]

进阶：

你可以优化你的算法到 O(k) 空间复杂度吗？

#include <iostream>
#include <vector>

using namespace std;

/// Simulate Pascal Triangle
///
/// Time Complexity: O(rowIndex^2)
/// Space Complexity: O(rowIndex^2)
class SolutionA{
public: 
    vector<int> getRow(int rowIndex){
        vector<vector<int>> res(rowIndex+1, vector<int>(rowIndex+1, 1));
        for(int i=2; i<=rowIndex; i++)
            for(int j=1; j<i; j++)
                res[i][j] = res[i-1][j-1] + res[i-1][j];
        return res[rowIndex];
    }
};

/// Simulate Pascal Triangle
///
/// Time Complexity: O(rowIndex^2)
/// Space Complexity: O(rowIndex)
class SolutionB{
public: 
    vector<int> getRow(int rowIndex){
        vector<int> up(rowIndex+1, 1);
        vector<int> down(rowIndex+1, 1);
        for(int i=2; i<=rowIndex; i++){
            for(int j=1; j<i; j++)
                down[j] = up[j-1] + up[j];
            up = down;
        }
        return down;
    }
};

void print_vec(const vector<int>& vec){
    for(int e: vec)
        cout << e << " ";
    cout << endl;
}

int main() {

    print_vec(SolutionB().getRow(3));

    return 0;
}

翻转字符串里的单词

给定一个字符串，逐个翻转字符串中的每个单词。

示例 1：

输入: "the sky is blue"
输出: "blue is sky the"

示例 2：

输入: "  hello world!  "
输出: "world! hello"
解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的·字符不能包括。

示例 3：

输入: "a good   example"
输出: "example good a"
解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

说明：

• 无空格字符构成一个单词。
• 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。
• 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

进阶：

请选用 C 语言的用户尝试使用 O(1) 额外空间复杂度的原地解法。

#include <iostream>
#include <vector>

using namespace std;

/// Reverse then reverse:)
/// Time Complexity: O(n)
/// Space Complexity: O(1)
class Solution
{
public:
    string reverseWords(string s)
    {
        int start = nextNonSpace(s, 0);
        s = s.substr(start);

        start = 0;
        for (int i = start + 1; i <= s.size();)
            if (i == s.size() || s[i] == ' ')
            {
                start = nextNonSpace(s, i);
                if (start != s.size())
                    s = s.substr(0, i) + " " + s.substr(start); //除去字符串中多余的空格。
                else
                {
                    s = s.substr(0, i);
                    break;
                }
                start = i + 1;
                i = start + 1;
            }
            else
                i++;
        reverse(s, 0, s.size() - 1);
        start = 0;
        for (int i = start + 1; i <= s.size();)
            if (i == s.size() || s[i] == ' ')
            {
                reverse(s, start, i - 1);
                start = i + 1;
                i = start + 1;
            }
            else
                i++;
        
        return s;
    }

private:
    int nextNonSpace(const string &s, int start)
    {
        int i = start;
        for (; i < s.size(); i++)
            if (s[i] != ' ')
                return i;
        return i;
    }
    void reverse(string &s, int start, int end)
    {
        int i = start, j = end;
        while (i < j)
            swap(s[i++], s[j--]);
    }
};
int main() {

    string s1 = "the sky is blue";
    Solution().reverseWords(s1);
    cout << s1 << endl;

    string s2 = "";
    Solution().reverseWords(s2);
    cout << s2 << endl;

    string s3 = " 1 ";
    Solution().reverseWords(s3);
    cout << s3 << endl;

    string s4 = "   a   b ";
    Solution().reverseWords(s4);
    cout << s4 << endl;

    return 0;
}

反转字符串中的单词 III

给定一个字符串，你需要反转字符串中每个单词的字符顺序，同时仍保留空格和单词的初始顺序。

示例 1:

输入: "Let's take LeetCode contest"
输出: "s'teL ekat edoCteeL tsetnoc" 

注意：在字符串中，每个单词由单个空格分隔，并且字符串中不会有任何额外的空格。

#include <iostream>

using namespace std;

/// Reverse in place
/// Time Complexity: O(len(s))
/// Space Complexity: O(1)
class Solution{
public: 
    string reverseWords(string s){
        int start = 0;
        for(int i=start + 1; i<=s.size(); )
            if(i == s.size() || s[i] == ' '){   //空格翻转无影响
                reverse(s, start, i-1);
                start = i+1;
                i = start + 1;
            }
            else 
                i ++;
        return s;
    }
private: 
    void reverse(string& s, int start, int end){
        for(int i = start, j = end; i<j; )
            swap(s[i++], s[j--]);
    }
};

删除排序数组中的重复项

给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

示例 1:

给定数组 nums = [1,1,2], 

函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 

你不需要考虑数组中超出新长度后面的元素。

示例 2:

给定 nums = [0,0,1,1,1,2,2,3,3,4],

函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。

你不需要考虑数组中超出新长度后面的元素。

说明:

为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以“引用”方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

#include <iostream>
#include <vector>
#include <cassert>
#include <stdexcept>

using namespace std;

/// Two pointers
/// Time Complexity:  O(n)
/// Space Complexity: O(1)
class Solution{
public: 
    int removeDuplicates(vector<int>& nums){
        if(nums.size()==0)
            return 0;
        
        int res = 1;
        int index = nextDifferentCharacterIndex(nums, 1);
        int i = 1;
        while(index < nums.size()){
            res++;
            nums[i++] = nums[index];
            index = nextDifferentCharacterIndex(nums, index + 1);
        }
        return res;
    }
private: 
    int nextDifferentCharacterIndex(const vector<int> & nums, int p){
        for(; p<nums.size(); p++)
            if(nums[p] != nums[p-1])
                break;
        return p;
    }
};

int main(){
    vector<int> nums1 = {1, 1, 2};
    cout << Solution().removeDuplicates(nums1) << endl;

    return 0;
}

移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

说明:

1. 必须在原数组上操作，不能拷贝额外的数组。
2. 尽量减少操作次数。

#include <iostream>
#include <vector>

using namespace std;

// Time Complexity: O(n)
// Space Complexity: O(n)
class Solution{
public: 
    void moveZeroes(vector<int>& nums){
        vector<int> nonZeroElements;

        // put all the non zero elements into a new vector
        for(int i = 0; i<nums.size(); i++)
            if(nums[i])
                nonZeroElements.push_back(nums[i]);
        
        // make nums[0...nonZeroElements.size()) all non zero elements
        for(int i = 0; i<nonZeroElements.size(); i++)
            nums[i] = nonZeroElements[i];

        // make nums[nonZeroElements.size()...nums.size()) all zero elements
        for(int i = nonZeroElements.size(); i<nums.size(); i++)
            nums[i] = 0;
    };
};
void printVec(const vector<int>& vec){
    for(int e: vec)
        cout << e << " ";
    cout << endl;
}
int main() {

    int arr[] = {0, 1, 0, 3, 12};
    vector<int> vec(arr, arr + sizeof(arr) / sizeof(int));
    Solution().moveZeroes(vec);
    printVec(vec);

    return 0;
}