动态时间规整DTW
1 概述
动态时间规整是一个计算时间序列之间距离的算法,是为了解决语音识别领域中语速不同的情况下如何计算距离相似度的问题。
相对于用经典的欧式距离来计算相似度而言,DTW在数据点个数不对齐的情况下微调时间从而能够计算距离。
DTW之所以能够计算数据点个数不同时间序列之间的距离,是因为DTW方法中时间序列的点可以一对多。
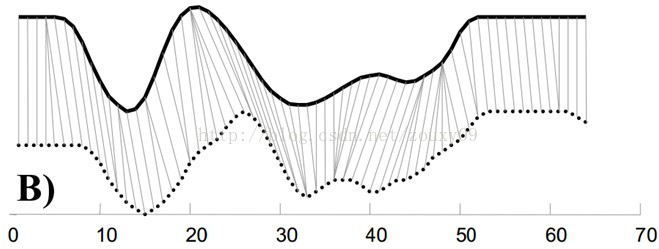
2 计算过程
用动态规划算法计算DTW距离的过程如下所示,计算不同长度时间序列T和R之间的距离(假设T、R长度分别为m、n)。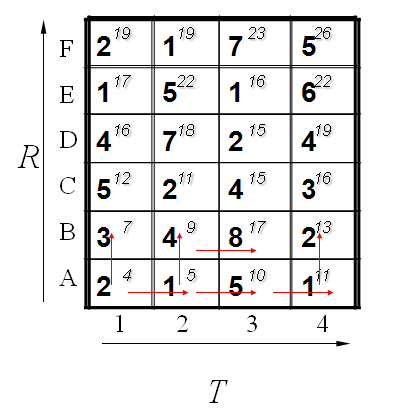 图中每一个小方格中粗体值是两两点之间的距离,可以是曼哈顿距离,也可以是欧式距离等等,而右上角的值是走到当前位置的累加距离,累加距离的计算公式如下:
图中每一个小方格中粗体值是两两点之间的距离,可以是曼哈顿距离,也可以是欧式距离等等,而右上角的值是走到当前位置的累加距离,累加距离的计算公式如下:
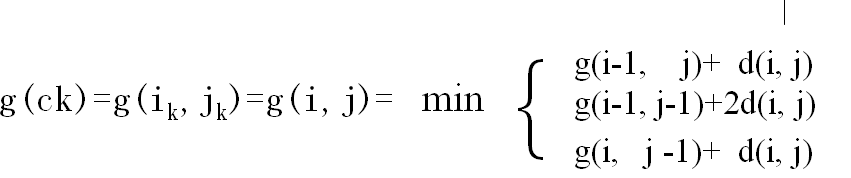
走动的方向如下图所示:
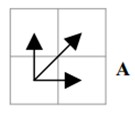
也就是说当前点的累加距离等于从当前点的下边的点或者左边的点或者左下边的点走到当前点的距离的最小值。根据公式从点(1,1)开始计算,直至计算到(m,n),最后点(m,n)的累加距离就是时间序列T和R的DTW距离了。而从点(m,n)开始回溯到点(1,1)的路径就是DTW计算的路径了。需要说明的是,不同的时间序列T和R,即使它们的DTW距离相同,而DTW路径也可能会不同。
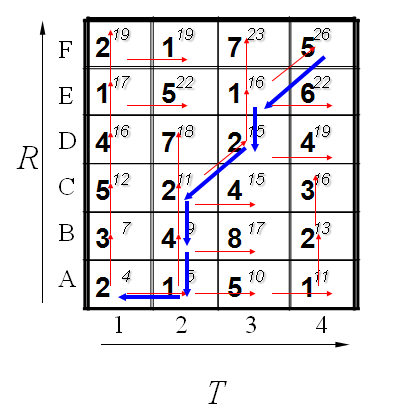
注意,从公式中可以看到,计算当前点的累加距离的时候,如果是从左下边的点走过来的,则当前距离还要乘以2,可以理解为走了两步。这样做的目的是使得计算任意两个长度为m、n的时间序列的DTW距离时,从(1,1)走到(m,n)的步数是一样的,都是m+n-2。这样大家走的步数都一样,DTW距离就可以表示时间序列之间的相似性了,这种距离也叫长度归一化后的距离。
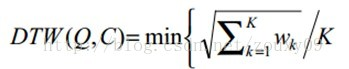
3 规整窗口
上面DTW计算的时候,路径是点(1,1)出发,向右上角前进。整个矩阵都会扫一遍,所有的点的累加距离都会计算出来。这种情况也叫作DTW, no Warping Window。
这样做的缺点是,如果最终的路径是从点(1,1)直线走到(1,F)再直线走到(4,F)。这说明T中的点1会对应R的A-F六个点,然后R中的F再对应T的2-4三个点。这样规整的跨度有点大了,就不再是微调时间序列中时间不对齐了,不符合实际呀。
所以又有了DTW with Warping Window,现在规整跨度,效果如下所示。只需稍微改动动态规划的代码的循环范围。
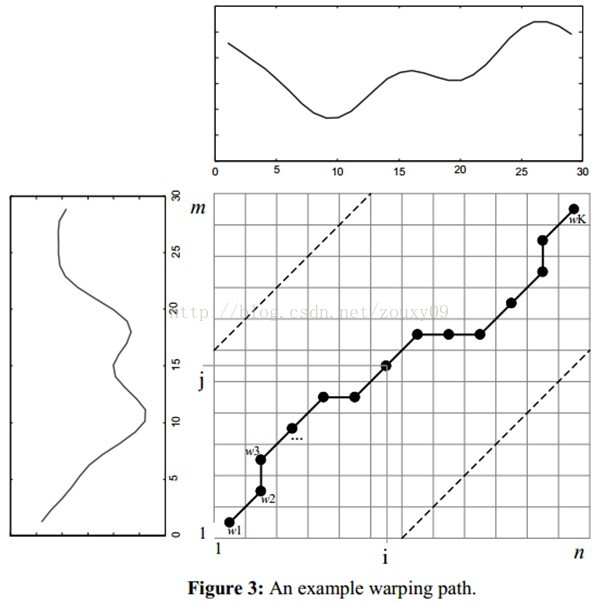
参考资料:https://www.cnblogs.com/Daringoo/p/4095508.html
https://en.wikipedia.org/wiki/Dynamic_time_warping