长时间地呆在解决数学问题的世界里,反而会让你看不清楚数学的本质,或者数学的根本性的东西。这个观点,陈省身(Shiing-Shen Chern)和陶哲轩(Terence Tao)都表达过。陈省身在谈论纳什(John Nash, 电影《美丽心灵》的主角,诺贝尔经济学奖得主)的时候就反复提到:John Nash当然是个出色的数学问题的解答者,一天到晚都在做题目。可是,他真的是不懂数学。而陶哲轩在回顾自己的早年经历也这样说:在做数学研究之前,整个对数学的工作就是不断地去做题目,以为解决一个又一个的难题,就是数学家一辈子干的事情了。直到自己真正走上数学家的道路,才发现,那时候的自己根本不懂数学。
戏剧的隐喻
在数学当中解决问题,很像是做programming的人在解决算法问题一样。这是领域中最难吭的骨头之一,也同时是挑战智商的舞台,是享受心智的荣耀的最佳场所。但从更加宏观的角度来看,这些事情虽然有一定的重要性,但做出的贡献毕竟比较微观,属于:在别人搭建好的舞台上演戏。你当然可以专注于去解决特定舞台上的重要问题,甚至去解决一些各个舞台都通用的技术问题。可是,你能否从零开始搭建起一个舞台,能否构建出一个精彩的故事,能否将精彩的故事从其它形式恰如其分地转移到你熟悉的场景,才是戏剧最关心的问题。
让我们来问一个幼稚但却微妙的问题:为什么说这才是戏剧最关心的问题?为什么灯光、造型、片子的剪切艺术,不是戏剧最关心的问题?
因为,戏剧的故事,舞台所传达的故事内涵,才是人们真正关心的。你这个戏剧是否能够继续在社会中存活下去,取决于是否有源源不断的观众前来观看,即:是否有社会中其它成员的关注。而故事以及故事的展现方式,才是吸引这些观众的核心。戏剧的价值在于它能够提供一种媒介,充分地表达和探索那些生活表面之下潜藏的真相,用极端的戏剧冲突极集中现那些隐藏的秘密。所以,这些精心设计的故事和表现方式所提供的揭示生活真相的服务,是让戏剧赖以生存的根本。而那些舞台技术细节,是构建故事的技巧。它重要,但却不是根本与核心。
总结起来,什么东西才是一个领域的核心价值呢?就是这个领域,能够为世界提供的不可替代的东西。如果这个领域所提供的东西,不再受到社会中其它成员的关注,它便会走向枯萎,便会死掉。
那么同样的,仅仅在数学中做题目,在计算机中做算法,对于各自的行业来说它重要,但却不是核心。过分地陷入这些过程,会让你一叶障目,陷入到这些微观细节之中。无论数学还是计算机,它的核心价值是提供一种供其他领域使用的工具,或者一种帮助其它领域梳理细节的服务。
计算机科学的认知
对于计算机来讲,它的本质在于运用机器来解放人类的生产力,也就是帮助一个个的人干活儿,特别是那种单调乏味的机械性的活儿。那么以此为标准,对于其它领域的人来说,运用你的计算机技能,通过printf不断地输出具备固定格式的短信的价值,要大于你对复杂算法的研究。因为这里的重点依旧在于,你是否把握住了你这个行业能够在世界中存在的核心:能否帮助人类干活。至于华丽的专业名词,诸如大数据、人工智能、深度学习、设计模式等等,其实都不是重点,或者说,它们彼此之间其实并没有一个高贵与低贱之分。你不能说研究深度学习的人比研究古老的关系数据库存储的人来得高贵,或者写for循环的人就比只写printf的人高贵。单看这些说辞,会觉得很荒谬,因为它完全没有抓住重点。重点在于你写出的代码或者弄出来的产品,是否对你当前的服务对象有价值有帮助。它是否能够帮助你当前的服务对象,更好地解放生产力。
如果继续用之前例子来说,对于需要重复发送短信的人来说,写出printf是核心,因为它解决了这个业务问题,不用再让用户做机械的发送动作。而一堆for,只是循环却不输出,并不会对业务起到半毛钱的效果。同样的,如果你服务的对象,仅仅是一个工厂,那么运用Excel的各种奇淫巧技,或许更能得到上司的亲耐。可你非要在工厂里面,部署Google那样的计算机集群,那估计你离被开除也就不远了。
这里想要说的是,如果纯粹从技术的角度看,不同技术之间其实是不存在好坏高下之分的,因为它仅仅是一个个客观的知识或者知识规律的总结。真正有高下好坏之分的,在于你的技术应用于业务的合理性、恰当性与优良性。可往往,身陷技术细节的人,会迷失或者自嗨在自己的领域,以自己的流行名号作为高人一等的资本。可这些名号仅仅是“表”,是外在的“名”,它无法撼动核心价值。重要的是,面对你要处理的业务和要服务的客户,选择什么技术工具是合适的。使用什么样的技术组合才能更高效、更优雅地解决用户的问题。
数学的认知
对于数学来讲,这样的认知和思维方式是相同的。数学的作用在于提供一种严格的定量讨论的框架。它的理论成果,用于从另一个角度去梳理事物之间的数量和变化关系,让整个问题的讨论,变得更精确、更严密。而不是闷头学习基础知识,为更加深奥的理论做铺垫。等铺垫结束,继续去钻研更深奥理论中的难题,或是为构建更深奥的理论做准备。
毋庸置疑,把当前的材料,进行加工和组合,自然会变成更加深奥复杂的东西。可是,为什么要构建这些理论呢?为什么要做这样的组合与粘连呢?没人可以限制你做任意的组合。但是,对其他领域的贡献和作为工具性的好使程度,是衡量你的组合是否有意义的一个标准。
我想,更有意思的问题是,我为什么要做这样的组合,为什么要去这样搭建一个数学框架,为什么那样不可以?从这些问题的回答中,你会明白数学对生产力的贡献,它最核心的基本价值在哪里。
让我们用自然语言处理(NLP)的例子来做一些说明。
如果想要根据文本本身,来进行语义的推断或者分类,一个重要的基础便是提供评价关键词的重要性的指标。这样的指标在不同的模型下有不同的体现。其中一种方式,是运用词袋(Bag of Words)模型,将一个文本向量化。运用一个重要的参考指标TF-IDF,来衡量这个关键词的对目标文本的重要程度。其中:
-
TF是Term Frequency,用于衡量这个词在目标文本中的出现频率:
-
IDF是Inverse Document Frequency,表示这个词在其它文本中出现的频率。
那么,一个粗略的TF-IDF指标便是:
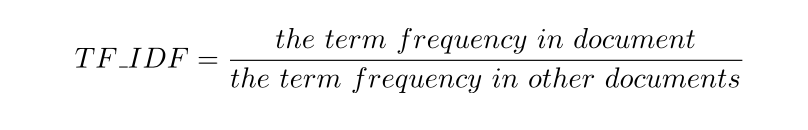
这个词在文本中的出现频率这个词在其它文本中出现的频率
直接看这两个定义会让人一头雾水,让我们从另一个角度来考察一番。一个词对于目标文本是否重要,一个质朴的想法是看它在这个文本当中出现的频率是否够高。你可以粗略地认为,它在这个文本中出现的频率越高,这个词就越能够表征这个文本的含义,也就是越重要。那么,TF就可以以正相关的方式,体现在TF-IDF的指标中。
而如果这个词是类似于the这样的常见却又没什么含义的词汇,它就不能作为目标文档中的意义表征。那么怎么衡量它是否是一个常见又没有实质含义的词汇呢?一种直观便是用它在其余文本中出现的次数来做表征。如果它越多的在其它文本中出现,那就越是说明这个词对于目标文本来说是不重要的。于是可以在TF-IDF中以倒数的形式呈现出来。这样,就解释了上面这个粗浅的公式。
但回到我们之前的那个问题,为什么这里一定是这样的公式?其合理性在哪里?换一个行不行?
例如,如果单词A在文本中出现100次,单词B出现200次,那是不是说单词B的重要性就是A的2倍?为它加一个对数来做平滑,是不是可以?如果这个词在其它文档中出现的次数都为0,那上面这个指标TF-IDF不就会出现分母为零的情况吗?应该怎么解决这个问题?为它们预先增加一个1?还是应该增加多少?
面对一个现实问题,或者当数学真正运用在其它领域时,其重点不在于哪个公式是对的。因为,每一个公式表征的是每一种对现实的认知与偏见,它对应到一个数学模型。而所有模型,都必然是与你研究重点相关的一种近似和简化。不存在正确的模型,只存在更好更优良的模型。数学所提供的,正是如同软件一般的工具模块。帮助你剖析问题,将你所关注的要点,以更加细密的方式展现出来。
不是说在模型中运用了微积分就比仅仅使用四则运算更高明。也不是说,你的模型中用到了现代数学或者集合论的抽象,就更加酷炫先进。这些都只是表,如同计算机的for循环和printf。重要的在于:运用了数学某个理论分支后,它所搭建的框架,是否将待解决的问题梳理得更清晰?在这样的梳理之下,这些问题是不是得到了更好的表述和说明?在这样的表述下,我关心的问题是不是更容易被解决?
正如关于世界地图拼图的故事所展现的:直接拼凑世界地图是困难的,但如果它的反面恰好是一个人像,世界地图将会因为背面人像的成功拼凑而得到更容易的实现。
那么数学这个理论工具的作用便是如此。它为其它领域提供一种独特的定量分析视角,将问题的细致末节挖掘得更深,考察得更仔细。一旦将一个东西被纳入到数学框架中做考虑,它就会像自然光被三棱镜分解一样,被数学框架做最精细的剖析。数学框架将每一个逻辑点分门别类地摆放好,以便更加清晰地凸显出事物内在逻辑的自洽性。这个工具本身不是用来评判或者增加原有材料的价值,而是作为一个客观的观察工具(好比三棱镜、好比望远镜),将事物内部复杂而隐秘的逻辑脉络完整呈现。这是这个工具真正厉害的地方。
越是理论、抽象的东西,越不容易看出应用方式的困难和解决问题的困难之间的区别。前者是一个宏观的方向性的东西,后者是一个深入的执行性的东西。而境界差距,就体现在对前者的把控和后者的适当运用。
为什么这个地方要用除法,为什么这个地方要取对数?
对深陷理论的人来说,ta只会从一种角度去寻找答案:如何根据上下文,运用严密的逻辑,推导出一个答案。从未尝试考虑:是不是因为我想要在这里发挥一个平均的作用;想要给它一个相反的用力效果;又或是计算太复杂,不如取个对数让它简单些的外部理由。而只是钻入到更深奥的理论中,看这个问题是否在其它理论中有个说法。
这其实体现了一种知识上的奴性。你只是不断地在寻找paper、寻找已有理论,去佐证一个模型或公式。而从来不会根据自己的实际需求,从你对业务的理解、对所要解决问题的认识,去评判模型的优劣,评价公式恰当与否。
数学的历史早已向我们说明,实践是先于理论的。微积分先是在工业中得到熟练运用,然后才是在很长的时间后被数学家们完善,成为一套牢固的理论。为什么数学的历史、科学的历史会这样发生?因为数学的职能是为了将一个问题剖析得更清晰而存在的,是以实际问题为驱动为导向。如果没有要解决的问题,你空拿屠龙宝刀有何用?龙都没有了,到哪里去运用你的屠龙之术?如果你服务的对象需要的是对家畜的屠宰之术,你绚烂的屠龙之术又于事何补?
所以,不能仅仅是从数学的内部去考虑问题,要多从外部去做宏观的思考:为什么我要做这个假设,为什么我要这么去构建一个公式,换一种方式行不行。没有这样的素养,面对新的未被开坑的领域, 没有任何教科书和现成公式作借鉴,你只能茫然无措。
数学的理论成果,正是一个个的建筑基石——building block。它们好比是设计师手中积累的素材。总是累计素材或者考量素材的制作方式是不够的。最后的临门一脚,需要将这些素材通过尝试和实验,巧妙地连接起来。
面对一个个数学building block,你可以真正地把它们当做乐高积木。用它们去做各种拼凑与尝试,看你组合出来的成果是否有利于你问题的解决和阐述。没有人知道哪种组合方式是恰当的。你需要做的是根据直觉、业务的理解,挑选出一些block,搭建好雏形,然后开始试验。根据试验所反馈的结果,来修正自己积木的搭建方式。如此往复,不断地打磨自己建造的数学模型,从而构建出适于解决当下问题的顺手工具。