
笔者一个数据结构的蒟蒻还是奇迹般的搞明白了splay的基本原理以及实现方法,所以写下这篇随笔希望能帮到像我当初一脸懵逼的人。
我们从二叉查找树开始说起:
二叉查找树是一棵二叉树,它满足这样一个性质:所有小于当前节点的点都在该节点的左子树上,所有大于当前节点的点都在该节点的右子树上。对于和当前节点一样大的点,我们有两种方法,一种是直接默认它到右子树上去,但是这样会造成空间的浪费。我们有一种比较好的操作是设置一个权值数组,如果出现了这种一样的情况,就直接把这个点的权值+1就可以了。
手绘了一棵二叉查找树:
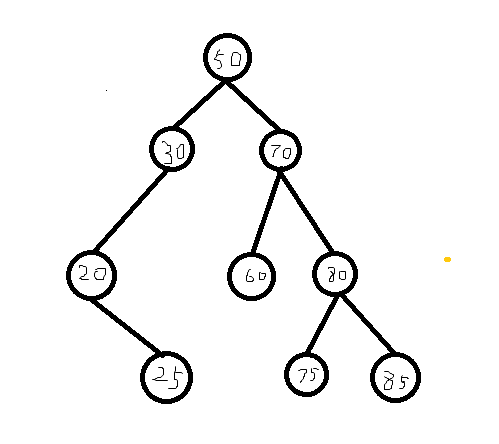
那么这棵树有什么用呢?
我们先来看这样一道题吧:
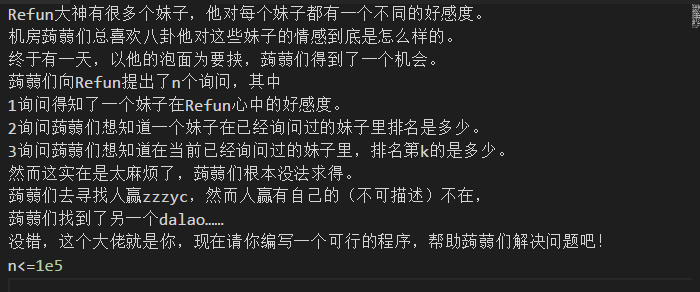
很明显,这个题我们可以直接用最高级的数据结构——数组实现,直接全读进来排个序什么的就直接OK了。
但是出题人就是想让这个题变得难一点,他使这个题变成了一边插入一边询问。很明显,刚才那个方法萎了,现在我们就要引入我们的二叉查找树了。
显然,我们可以很轻松的使用二叉查找树来完成插入这个工作。重要的是完成询问2和3。
先来看询问2吧:由于二叉查找树的性质,我们比较询问的妹子的好感度与当前节点的好感度,如果少了那就向左查找,多了就向右查找。我们最终总是会找到的。然后这个妹子前面有k个人,那么这个妹子就排名为k+1.
然后是询问3:我们比较每个节点的k值和当前的k值,依然按照二叉查找树的性质比较大小就可以了。
这样我们就可期望O(nlogn)出解来八卦掉Refun大神。
但是题是死的,人是活的,出题人是毒瘤的,每种这样的题目总会有这样的数据:给出的插入完全有序,结果我们的两个查找一下子全成了n的复杂度。
就想是这样一棵树:
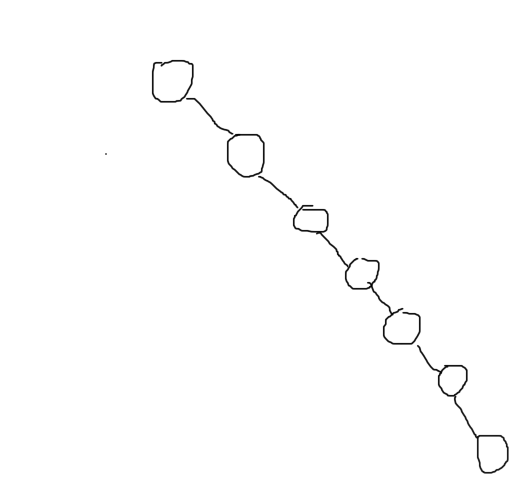
你看这棵长坏了的树。那如何解决这种问题呢?自然是使这棵树平衡起来,具体实现有treap,splay等等。
现在我们就引入今天的正题——splay
splay
首先声明一些变量:

和一些操作:
求当前节点是左?右?儿子:
inline int get(int x) { return ch[f[x]][1]==x; }
清零操作:
inline void clear(int x){ ch[x][0]=ch[x][1]=size[x]=f[x]=key[x]=cnt[x]=0; }
更新size值的操作:
inline void update(int x) { if(x){ size[x]=cnt[x]; if(ch[x][0]) size[x]+=size[ch[x][0]]; if(ch[x][1]) size[x]+=size[ch[x][1]]; } }
然后就是splay的关键操作了,旋转。
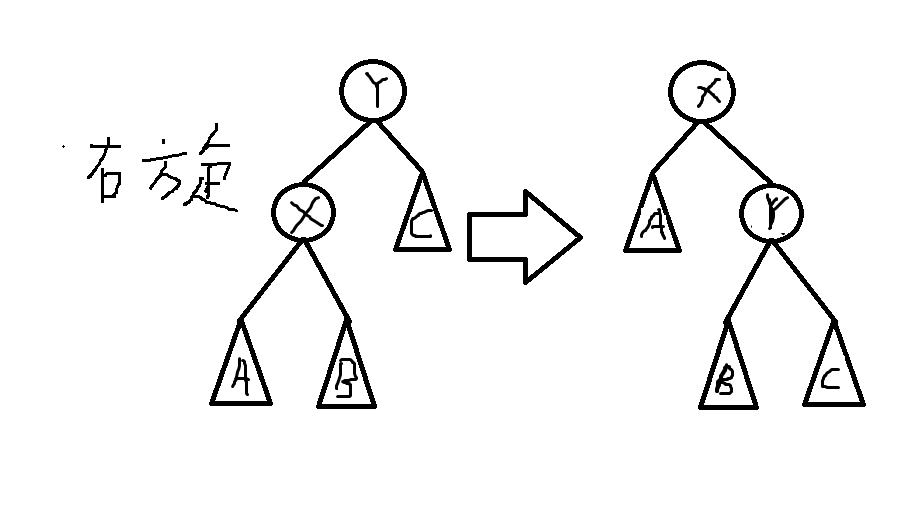
有人可能有疑问了,这旋转有个P用,看上去啥都没改变啊。然而实际上,这旋转就是成功把x向上提了一个位置,而我们的目标就是像这样一步步把一个节点向上提到他的一个祖先下面,或者就这么变成了根。
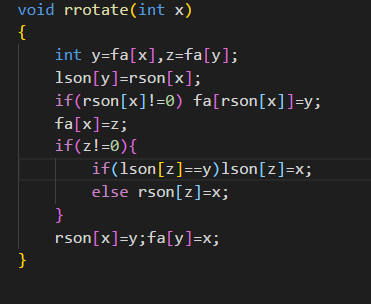
那这个右旋应该怎么样实现呢?我们分三步来解释:
一:我们先看看x有没有右子树,如果有的话,让它成为y的左子树,同时让它认y做爹。
二:我们看看,这个时候x就没有右子树了,我们就让y认x做爹,然后让y作为x的右子树。
三:我们再看看,y有没有爹,如果有的话,假定这个爹叫z,那么让x认z做爹,并且要与y的左右子树的性质一致。
贴一段代码,看看应该挺好理解的:
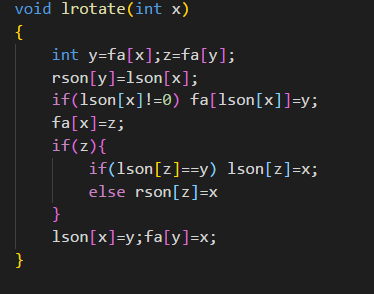
至于左旋和右旋很像,不过代码笔者还是码了的:
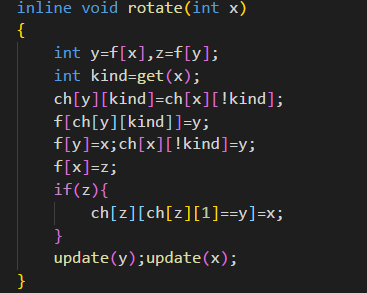
至于实际操作的时候,我们自然不可以把这俩玩意分开,实现起来很复杂,所以用ch数组的两维代表左右儿子,通过一个综合函数来实现这两个函数。并且在旋转完了之后要紧接着update维护一下。
这样我们最基础的旋转就已经搞定了,接下来我们要实现splay的关键操作,splay。
splay的目的在于把一个节点一直转到一个给定的节点底下,然后,一般人们都直接旋转到根。
可以用一个简短的代码概括一下
至于怎么旋转,我们要分情况讨论:
如果x,y,z三个点在同一个直线上的话,那么就要先旋转y,否则我们就先旋转x。如果不这么做的话,就会造成树的失衡。
那么我们可以先看一下繁杂的代码,不过好理解是真的:
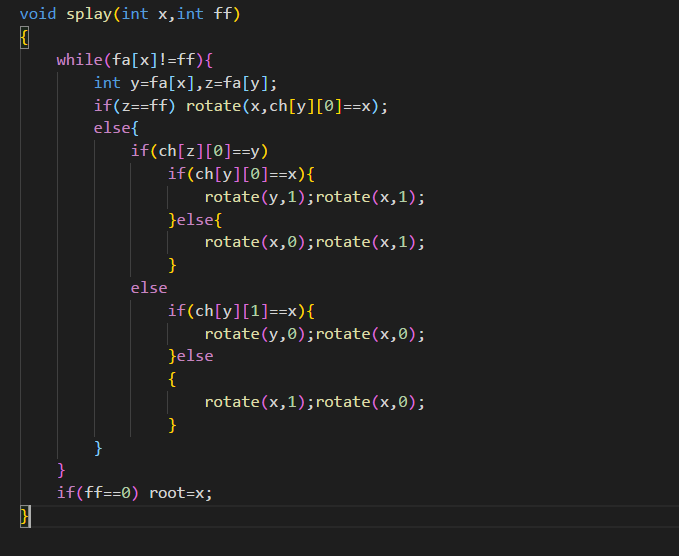
很明显的是,这个代码很长,不过看上去应该还是比较清楚的,下面提供一种简洁很多的版本:
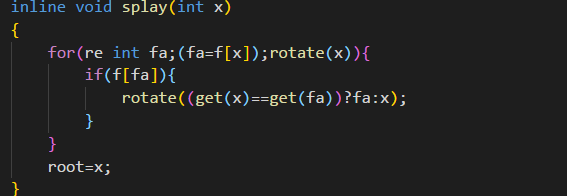
对于直接旋转到根的情况来说,这两个代码是完全等价的。
然后就是依题目而定的具体操作了,这里我们以各大OJ上都有的一道普通平衡树的模板题来示例。
首先看一下他需要让我们进行的操作

那我们就一步步的看这些操作都怎么实现吧:
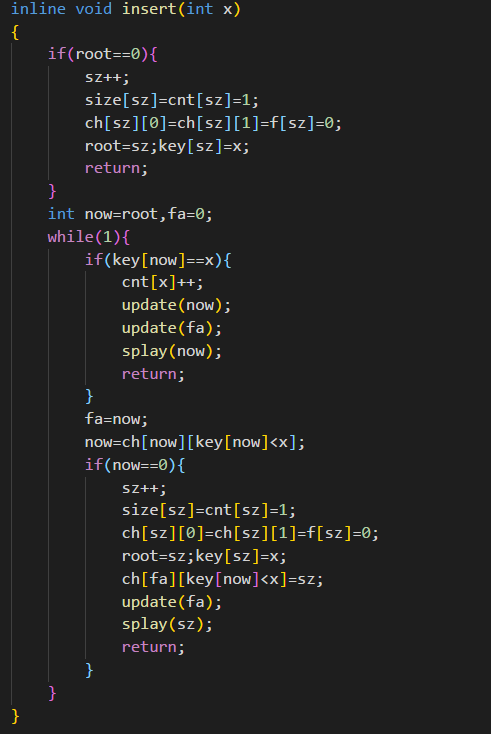
1.插入一个数:都还记着笔者刚刚开始说二叉查找树的时候就已经说过了插入是一个很简单的工作了吧。。
(1):首先对于root==0时,明显树是空的,进行一些特殊操作直接退出来就行了。
(2):对于root!=0时的情况,如果在向下寻找的时候我们寻找到了一个和它一样大的点,我们就可以直接把它的权值加1,然后update维护下它和它的爹,再splay一下。
如果我们直接找到了最底下,那没什么好说的了,把树的大小+1,由于它是最底下的节点,没必要update自己,直接维护一下父节点,splay一下就行。
代码总是有的,笔者就是这么的善解人意:
删除一个数比较麻烦一会再说;
2.查找一个数的排名
这里的操作就和二叉查找树越来越像了。
(1):如果当前节点的数值比我们现在的小,那么不用进行其他的任何操作,我们直接继续向左子树查找就可以了。
(2):如果当前节点的数值比我们现在的大,那么我们就把返回值加上左子树以及根的大小,然后向右子树查找。
还有一个,找着了之后要splay一下。。
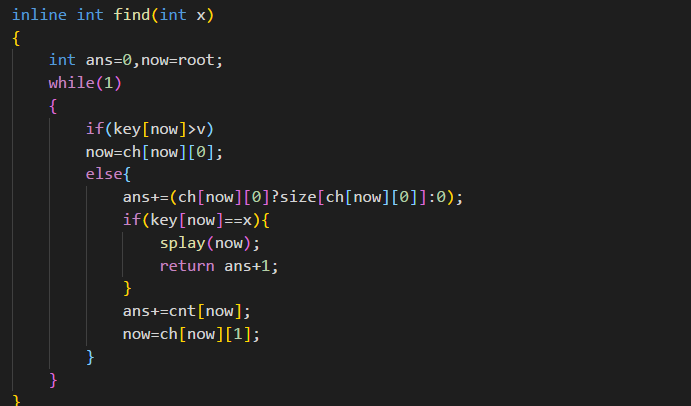
3.查询一个排名的数
(1):首先一上来先看看正找着的这个点有没有左子树,如果有的话,并且它的大小比x大,那么就向左查找,否则向右。
(2):向右查找的时候,注意把节点的大小和右子树的大小都记录下来,以便判断是否要继续向右子树查找。
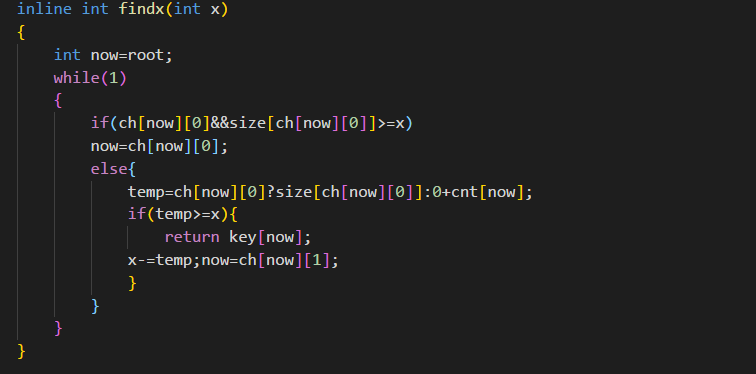
3:求x前驱和后继
这个操作比较容易的吧,不过得想对。
对于这两个操作,我们直接先插进去x,然后求出它在树上的前驱和后继,自然也就是它的前驱和后继,然后把它删掉就可以了。
然后我们发现,在插入这个x的时候我们把它旋转到了根节点的位置上,所以前驱就是它左子树最右的节点,就是先向左找一下,然后一直找到没有右儿子了为止,同理后继就是它右子树最左的节点。(不知道为什么建议向上翻翻找着二叉查找树的定义仔细阅读)。
至于怎么找,不想说了,实在不明白的就看代码明白吧。。
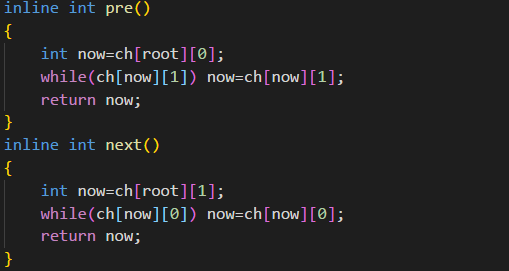
5:删除操作
这个操作还是比较麻烦的,注意的地方也教前面的操作多一点。
(1):为了方便接下来的操作,先把x旋转到根节点,随你怎么转过去。
(2):然后分情况讨论,现在x已经是根节点,如果它的权值不为1,那就好办,-1之后返回就行了。
(3):然而肯定有很多是1的,怎么办?如果x一个孩子都没有,把x删了就行,反正树上就它一个节点。
(4):如果x只有任何一个儿子,那么把x删了,直接让儿子当爹就行。
(5):如果有两个儿子的话,首先我们要先选一个根,自然是x的前驱或后继,这里我们选择前驱,然后把前驱旋转到根节点,然后再把x原来的右子树当做它的右子树,update维护一下就行。
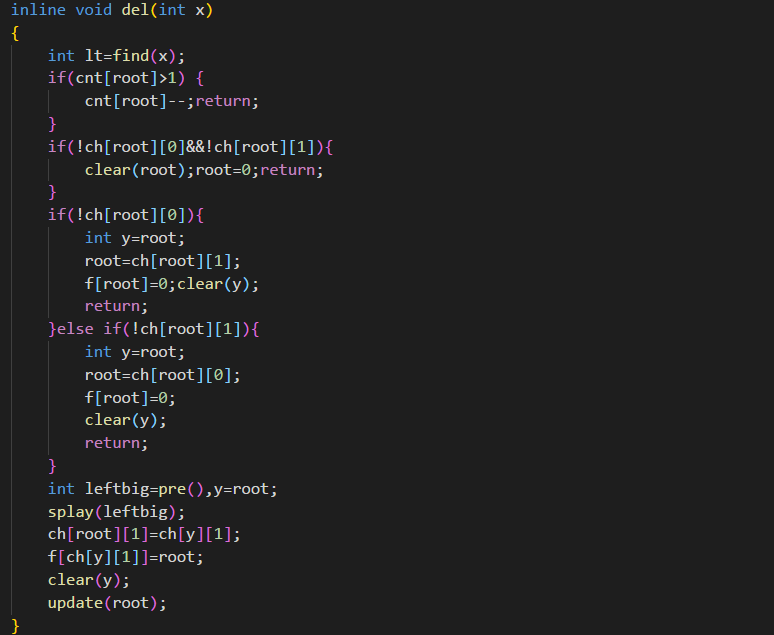
这样一来,这个题就这么结束了。
其实splay整个操作都是基于二叉查找树的,我们的rotate操作很明显是符合二叉查找树性质的。
看上去完了?
没有,我们还要说一个点.
用splay实现区间翻转
其实,要操作起来有很多种可以用splay实现的方法了,这里介绍一种看上去正常实现起来比较容易的。
我们根据二叉查找树的性质,可以看出假如我们要在Splay中修改区间的话,可以先查找siz值为l与r+2的两个节点,将一个旋转到根,另一个旋转到根的右儿子上,则要修改的区间就是根的右孩子的左子树,直接打标记即可。
为什么这么旋转就可以?先上图: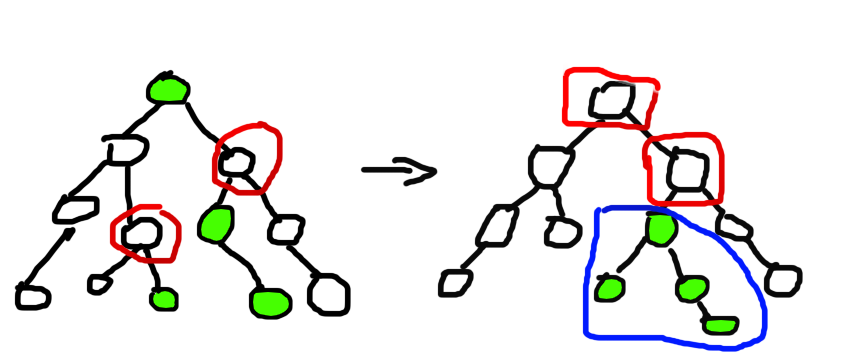
理解一下,红圈里的两个点就是我们要旋转的点,第二个图中蓝圈里的就是要翻转的区间,并且这样翻转完了之后它仍然与开始那个图的中序遍历相同。绿色的点就是我们要翻转的点。。为什么是这些点。。。因为要翻转的一定是比l的下标大比r+2下标小的点。
至于代码可以这么实现,不是一个很麻烦的事。
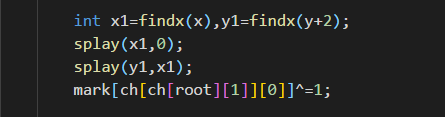
还有一个要说的是,我们做这个题建立平衡树的时候,是按照数组下标建树,而不是按照大小建树。所以很有必要放一下代码强调一下。
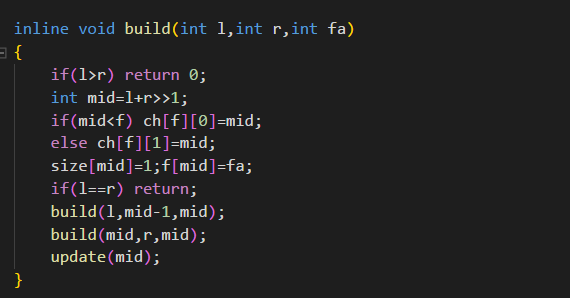
眼神好的人应该能看出来这份代码和下面的有些区别,事实上,这个代码能够一开始的时候建立出一个完美平衡树(虽然不久之后它就不那么完美了),理论上能够快一点吧。而下面的代码一开始很有可能建出来,额。。。一条链,不过很快也会splay掉了。
放上题目的完全代码了。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 #define re register 8 #define maxn 1000007 9 #define ll long long 10 #define ls rt<<1 11 #define rs rt<<1|1 12 #define inf 1000000007 13 using namespace std; 14 int ch[100001][2],f[maxn],cnt[maxn],key[maxn],size[maxn],mark[maxn],root,sz,data[maxn]; 15 inline int pushdown(int x) 16 { 17 if(x&&mark[x]){ 18 mark[ch[x][0]]^=1; 19 mark[ch[x][1]]^=1; 20 swap(ch[x][0],ch[x][1]); 21 mark[x]=0; 22 } 23 } 24 inline void clear(int x) 25 { 26 ch[x][0]=ch[x][1]=f[x]=cnt[x]=key[x]=size[x]=0; 27 } 28 inline int get(int x) 29 { 30 return ch[f[x]][1]==x; 31 } 32 inline void update(int x) 33 { 34 size[x]=size[ch[x][1]]+size[ch[x][0]]+1; 35 } 36 inline void rotate(int x) 37 { 38 int y=f[x],z=f[y]; 39 int kind=get(x); 40 pushdown(y);pushdown(x); 41 ch[y][kind]=ch[x][kind^1];f[ch[y][kind]]=y; 42 ch[x][kind^1]=y; 43 f[y]=x; f[x]=z; 44 if(z){ 45 ch[z][ch[z][1]==y]=x; 46 } 47 update(y);update(x); 48 } 49 inline void splay(int x,int tar){ 50 for(re int fa;(fa=f[x])!=tar;rotate(x)) 51 if(f[fa]!=tar){ 52 rotate(get(x)==get(fa)?fa:x); 53 } 54 if(!tar) root=x; 55 } 56 inline int build(int fa,int l,int r) 57 { 58 if(l>r) return 0; 59 int mid=l+r>>1; 60 int now=++sz; 61 key[now]=data[mid],f[now]=fa,mark[now]=0; 62 ch[now][0]=build(now,l,mid-1); 63 ch[now][1]=build(now,mid+1,r); 64 update(now); 65 return now; 66 } 67 inline int findx(int k) 68 { 69 int now=root; 70 while(1) 71 { 72 pushdown(now); 73 if(k<=size[ch[now][0]]) 74 now=ch[now][0]; 75 else{ 76 k-=size[ch[now][0]]+1; 77 if(!k) return now; 78 now=ch[now][1]; 79 } 80 } 81 } 82 inline void print(int now) 83 { 84 pushdown(now); 85 if(ch[now][0]) print(ch[now][0]); 86 if(key[now]!=-inf && key[now]!=inf) 87 printf("%d ",key[now]); 88 if(ch[now][1]) print(ch[now][1]); 89 } 90 int main() 91 { 92 int n,m,x,y; 93 cin>>n>>m; 94 for(re int i=1;i<=n;i++) 95 { 96 data[i+1]=i; 97 } 98 data[1]=-inf;data[n+2]=inf; 99 root=build(0,1,n+2); 100 for(re int i=1;i<=m;i++) 101 { 102 cin>>x>>y; 103 int x1=findx(x),y1=findx(y+2); 104 splay(x1,0); 105 splay(y1,x1); 106 mark[ch[ch[root][1]][0]]^=1; 107 } 108 print(root); 109 }
其实splay更多的是一种辅助的工具,理解了之后代码难度略小于treap(因为笔者现在还没搞懂treap),而且灵活多变,可以处理多类问题,至于常数大这个缺点,用各种玄学方式优化一下吧。。。