字符串模式匹配——KMP算法

KMP算法匹配字符串

朴素匹配算法

  字符串的模式匹配的方法刚开始是朴素匹配算法，也就是经常说的暴力匹配，说白了就是用子串去和父串一个一个匹配，从父串的第一个字符开始匹配，如果匹配到某一个失配了，就重新去从父串的下一个字符开始匹配，这样的算法虽然理解起来容易，但是算法的时间复杂度无疑是很高的，假如父串是一个很长的字符串，而字串恰恰不和父串匹配，那无疑是对CPU的迫害。

  下面贴几张图看看这种朴素匹配算法:

但是第四个出现失配，就得重新让字串去和父串的第二个字符匹配，发现第二个也不匹配，只能再次匹配第三个，如下：

  这样下来时间复杂度大大变高，但是通过上帝视角我们可以发现其实第二个完全不用试，但是计算机不知道啊，所以我们就需要一个更好的算法来解决这个问题，这个算法就是要在朴素算法的基础上额外告诉计算机哪些地方不用尝试，可能我上面的这个例子举得不太恰当，但是这个算法的额外功能就是告诉了计算机如果某个位置失配了应该去尝试哪个位置。

  

KMP算法——和计算机的友好交流

  前面我们说KMP算法其实就是告诉计算机如果某个位置失配后应该往哪个位置回溯。而这个功能的实现其实只需要一个next数组，而这个数组也恰恰是这个算法的核心所在。

next数组

  这个数组里面存储的就是字串中每个位置失配后应该回溯的下标。举个例子，比如第9个元素失配后应该回溯到第3个再次匹配尝试，那就应该是next[9] = 3，值得注意的是，我们定义的串这个数据结构一般没有0号元素，所以next数组一样，next[0]没有意义。

  next数组该如何实现呢？

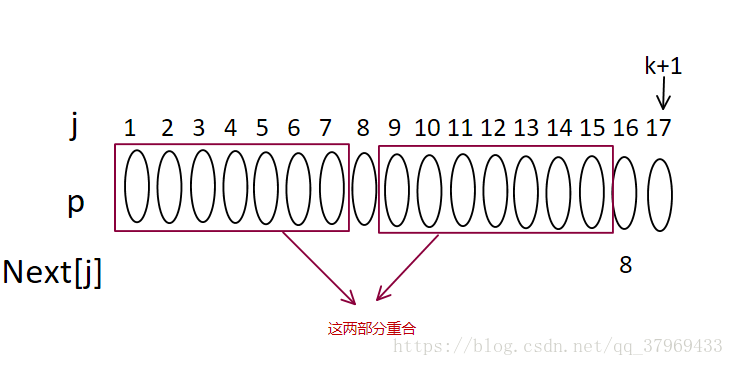
比如这块我们发现1-7和9-15都相等，而8和16不相等，那如果在第16个位置发生失配，就可以用1-7依次替代9-15的位置，用第8个再去匹配，如果匹配上了就继续往下匹配，未匹配就继续回溯。

代码实现（next数组）：

void get_next(string son, int* next)
{
	int i = 1;	 //下标
	int j = 0;	//回去的位置
	next[1] = 0;		
	/*因为字符串未设置0号元素，所以next从1开始，默认为0，你应该懂我意思吧，回溯到0，你可能会问：
	不是说好没有0号元素吗。你想啊，让字串的0号元素和父串的下一个匹配，难道不就是让字串的第一个和父串的
	下一个匹配吗*/
	while (i < son.len)
	{
  //如果这两个相等，即下标为i和j的元素相等，则当后面那个元素即i的下一个元素失配时，回溯到j的下一个元素，因为i和j的元素相等，所以保证了前面的一致，可以回溯
		if (j == 0 || getch(son, i) == getch(son, j))	
		{
			i++;  j++;			//精华，++后对应上面那句注释的	“当后面那个元素即i的下一个元素失配时，回溯到j的下一个元素”
			if (getch(son, i) == getch(son, j))		//这里是一处优化，如果++后还相等，那你回溯回去肯定还失配啊，就再次回溯到你回溯的回溯
				next[i] = next[j];
			else
				next[i] = j;
		}
		else			//如果不相等，就将j回溯，i不能变，因为i一个一个加给next数组每个依次赋值
		    j = next[j];
	}
}

KMP算法部分

  实现了next数组，剩下的就很简单了，利用next数组在失配时去回溯就ok了。

代码实现：

getch()函数是为了随机访问串

int kmp(string far, string son)
{
	int next[255];
	get_next(son, next);
	int index = 1;		//子串的下标索引
	for (int i = 1; i <= far.len; i++)		//遍历父串
	{	
		while (index <= son.len)
		{
			if (getch(far, i) == getch(son, index))
			{
				index++;	//如果匹配给子串+1
				if (index == son.len + 1)
				{
					printf("成功！
");
					return i - son.len + 1;
				}
				break;
			}
			else
			{
				index = next[index];
				if (index == 0)
				{
					index = 1;
					break;
				}
			}
		}		
	}
	printf("失败！
");
	return 0;
}