（一）引入—梯度下降算法
1. 线性假设：
2. 方差代价函数：
3. 梯度下降：
4. 
: learning rate
（用来控制我们在梯度下降时迈出多大的步子，值较大，梯度下降就很迅速）
值过大易造成无法收敛到minimum（每一步迈更大）
值较小且适宜的情况下，步子越来越小直到收敛（导数项为零） 
不再改变。
（注：每一次梯度下降，需完成多个的同步更新）
右侧计算后立即更新是不正确的，在计算时使用了新的，未实现同步。
（二）结合——线性回归模型
1.一元线性回归模型
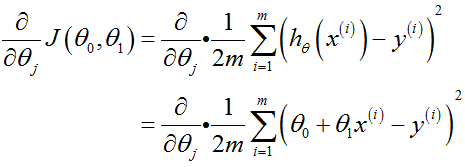
分别对
求偏导：
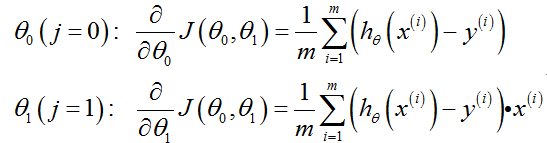
将导数项代回得梯度下降：
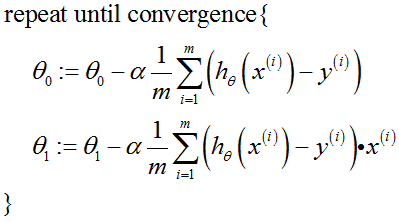
课堂注解：
2. 多元线性回归模型
（1） 多元线性回归假设函数形式：
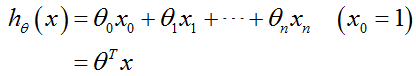（2）多元线性回归梯度下降算法表达式：
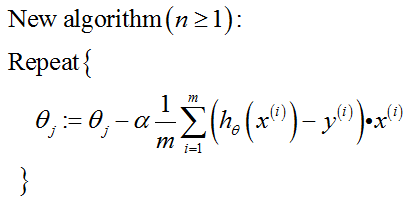
课程注解：
（三）Some Tips
1. 特征缩放：使梯度下降的速度更快，收敛所需的迭代次数更少。
假设我们有两个特征 
，在梯度下降的过程中，画出的参数等值线如下图。
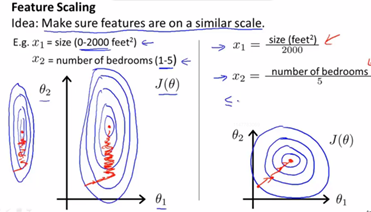
由图中红线可以看出，当 
值的scale（取值范围）相差很大时，梯度下降的的道路是曲折的，而当对数值进行处理后，梯度下降的过程变得很高效。所以我们在实际操作时，经常将特征的取值约束到-1到+1的范围内。（-1、+1两个数值并不重要，只是作为辅助作用将特征取值调整到合适范围）
有时我们需要将特征值“标准化”使其均值为0，其中
是训练集中特征值
的平均值，
是该特征值的取值范围（最大值-最小值）
2. 是否收敛（观察图像及收敛测试）
（推荐通过左侧图像观察梯度下降算法是否正常工作，而不是依靠自动收敛测试。）
3. 关于学习率
左侧两种情况出现的原因可能是
过大，然而如果
过小，收敛将极其缓慢。
（通常会尝试一些
值，如0.01、0.001，十倍取一个值，对于这些不同的值，绘制
随迭代步数变化的曲线，选择使
快速下降的
值，实际中常取三倍来找合适的值）
在训练模型对数据进行拟合时，我们可以自由选择使用什么特征，并且通过设计不同的特征，我们可以使用更复杂的函数去拟合数据，而不是只用一条直线去拟合。
（四）正规方程法
1. 正规方程法一步求出最小
（不需要特征缩放）
将矩阵X、向量y带入如下公式，（X：将第i条训练数据特征值
转置，作为设计矩阵X的第i行。y：把所有标签，如训练集中的所有房价数据，放在一起构成。）即可求出目标参数值。
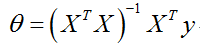
2. 正规方程法和梯度下降法优缺点比较
（n<10000选用正规方程法）
小结：我们可以看到，对于线性回归这个特定的模型，正规方程法能够成为一个比梯度下降法更快的替代算法，而在Logistics回归模型等一些其他更复杂的模型当中，正规方程法不适用。所以，我们应该掌握这两种方法，根据具体的算法、根据具体的问题，以及特征的数量，对这两种方法进行更好的应用。