Splay与LCT
本文介绍splay与lct的基本原理与应用
需要的前置知识:二叉排序树,树链剖分原理。
小菜鸡为了应付老师作业写的,诸多错误还请指教。
splay
二叉排序树
二叉排序树或者为空,或者具有下面的性质:若它的左子树非空,则左子树所有的权值均小于它;若右子树非空,则右子树所有的权值均大于它;左右子树均为二叉排序树。
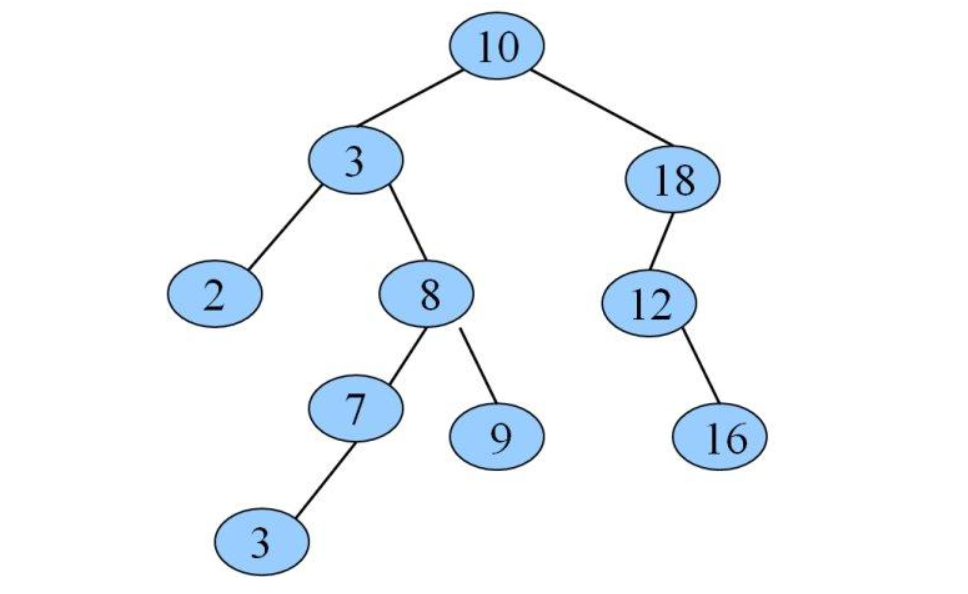
这样这棵树的中序遍历就是升序的,并且我们可以通过维护树上节点的size来动态地支持插入,删除,查询第k大,查询值的排名,找前继与后继等操作。很容易发现,这些操作的复杂度与树的高度相关,最优情况下它们都是log级别。
不过我们很容易构造出数据来使二叉搜索树退化成链,复杂度瞬间爆炸。
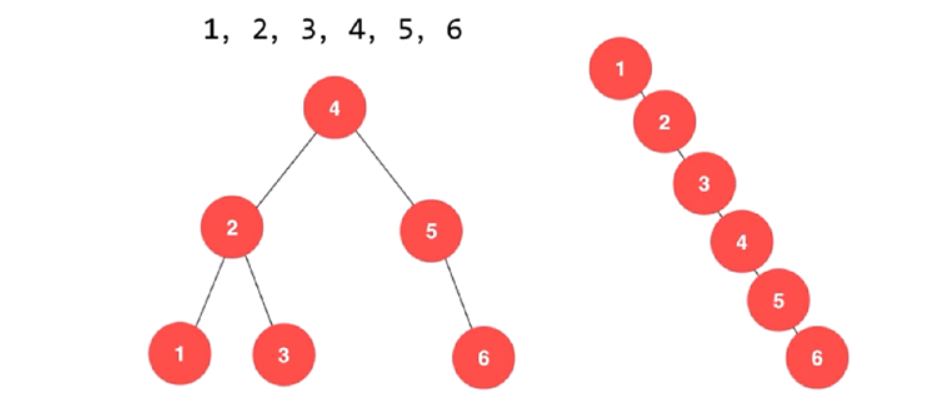
于是我们希望在保证二叉排序树性质的同时,改变树的形态,让树变矮,来保证复杂度,这样的数据结构有很多种,统称为平衡树。
splay
splay是算法竞赛里应用较广泛的一类平衡树。它通过旋转与伸展来保证树高。
旋转
定义:把左儿子旋至父亲的位置为右旋,把右儿子旋至父亲位置为左旋。

如上图将x右旋,分为三步:x的祖父变成x的父亲,y的左儿子变成x的右儿子,x的右儿子变成y. 这样中序遍历结果不变,我们改变了树的形态,还维持了二叉排序树的性质。
void rotate(int x){
int y=spl[x].fa,z=spl[y].fa;
if(!y) return;
int k = spl[y].son[1]==x; //判断左儿子还是右儿子
spl[x].fa=z;
if(z) spl[z].son[spl[z].son[1]==y]=x;
spl[y].son[k]=spl[x].son[k^1];
if(spl[x].son[k^1]) spl[spl[x].son[k^1]].fa=y;
spl[x].son[k^1]=y;
spl[y].fa=x;
update(y); update(x); //y与x所管理的子树发生改变
}
伸展
研究表明,倘若我们每次访问到(插入,查找,等等)一个节点时,都将其旋转至根节点,就能很大程度维护树的平衡。 但是伸展操作添加了一些东西:
令y为x的父亲。1:y是根,则直接将x旋转一次;2:y非根且x与y同为各自父亲的左儿子或同为右儿子,则先将y旋转一次,再旋转x;3:其他情况正常旋转。
研究表明,这样可以使x到根路径上的点深度大致减一半,并且使得所有操作均摊复杂度为log级别。
下面是将x旋转至想要的节点的代码:
void splay(int x,int goal){
int tmp=spl[goal].fa;
for(int f;(f=spl[x].fa)!=tmp;rotate(x)){
if(spl[f].fa!=tmp) rotate((x==spl[f].son[1])^(f==spl[spl[f].fa].son[1])?x:f);
}
if(!tmp) root=x;
}
find
在平衡树里找到x并将其伸展至根。这样的话什么找val的排名,前驱后驱都很方便了。
bool find(int valu){
int rt=root;
while(spl[rt].son[spl[rt].val<valu] && spl[rt].val!=valu)
rt=spl[rt].son[spl[rt].val<valu];
splay(rt,root);
if(spl[rt].val==valu) return true;
else return false;
}
其他的插入,删除等操作都和普通二叉排序树类似,区别在于每次插入一个点立即将其splay至根。
splay区间操作
splay可以说是区间操作的大杀器!比线段树还有用(不止一点半点)。考虑下面的问题:
维护一个数列,支持以下操作:1. 在数列第pos位插入一段给定的序列;2. 将当前序列第L位到第R位翻转;3.单点修改,区间修改。
这种问题在算法竞赛里基本只能用splay做。对于原序列,我们用每个值在序列里的位置作为平衡树上节点的权值。
操作1:找到平衡树上排名第pos的点x与第pos+1的点y,将x伸展至根,将y伸展至根的右儿子,根据平衡树性质,此时y的左子树为空,将给定序列建平衡树,此树接到y的左子树即可。
操作2:找到平衡树上排名第L-1的点x与第R+1的点y,同样将x伸展至根,y伸展至根的右儿子,那么y的左子树就是L到R的区间,对左子树的根打上翻转的懒标记。
操作3:单点修改视同区间修改,仿照操作2打懒标记。
int split(int x,int y){
splay(x,root);
splay(y,spl[root].son[1]);
return y;
}
题目
LCT
我们可以通过splay这个强大的数据结构来动态维护一个森林。
我们知道,对于一棵固定的树,我们可以用重链剖分(比较简单,没有学过的话参考洛谷日报:重链剖分)加线段树来支持其任意路径的权值修改与查询。
但是假如这颗树结构不固定,是动态修改的,那么线段树就不管用了。
也就是说对平面上的点我们要实现以下操作:1.若x,y不连通,连接x,y;2.若x,y有边,断开这条边;3.若x,y联通,修改路径上点的权值;4.若x,y联通,查询路径上点的权值和。
参照重链剖分的思想,我们通过实链剖分,用更灵活的splay来维护每条链,这就是link-cut-tree.
实链剖分
参照重链剖分,我们有以下定义:
实儿子:一个节点若有儿子,可指定其任意一个儿子为实儿子,那么其它的儿子都是虚儿子
实边:连向实儿子的边
虚边:连向虚儿子的边
实链:由一个虚儿子,不断经过实边直到不能连为止,所得的链
区别在于,这里的实和虚是可以动态转换的,而不是固定的。
LCT使用splay这样来维护一棵树:
1.每条实链存在且仅存在于一棵splay中,并且对其中序遍历所得的节点序列在原树中的深度严格递增
2.每棵splay的根节点通过虚边连向另一棵splay或者0,虚边通过连向父亲的单向边来表示。
确实有点绕,结合图来看一下:
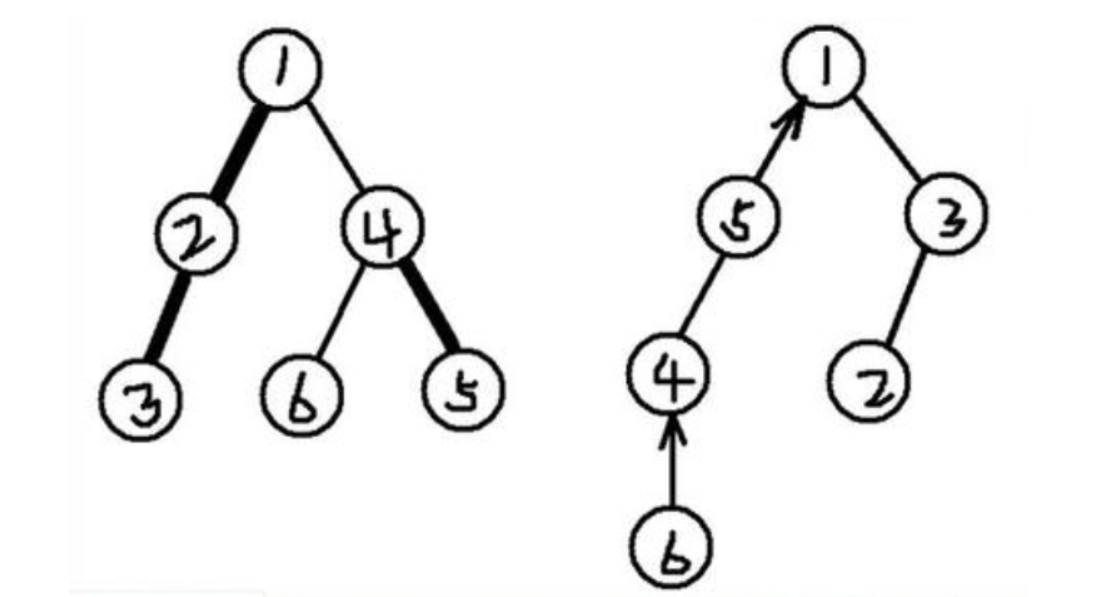
图中粗边为实边。那么树被剖分成三条实链:(1,2,3),(4,5),(6).
这三条实链根据各自节点深度关系形成三棵splay,每棵splay的根向另一棵splay连一条虚边(右图中的单向边),可以理解为虚边是两条链之间的边,而非点与点之间的边。
关于虚边的单向边存储,比如要x向y连一条虚边,那么spl[x].fa=y; 但是y的左右儿子都不是x.
下面介绍LCT基本操作:
access
LCT核心操作,作用是将节点N与原树根节点之间的链连成一条实链,那么有些实边需要变成虚边,有些虚边需要变成实边,这就体现了LCT的虚实变换。
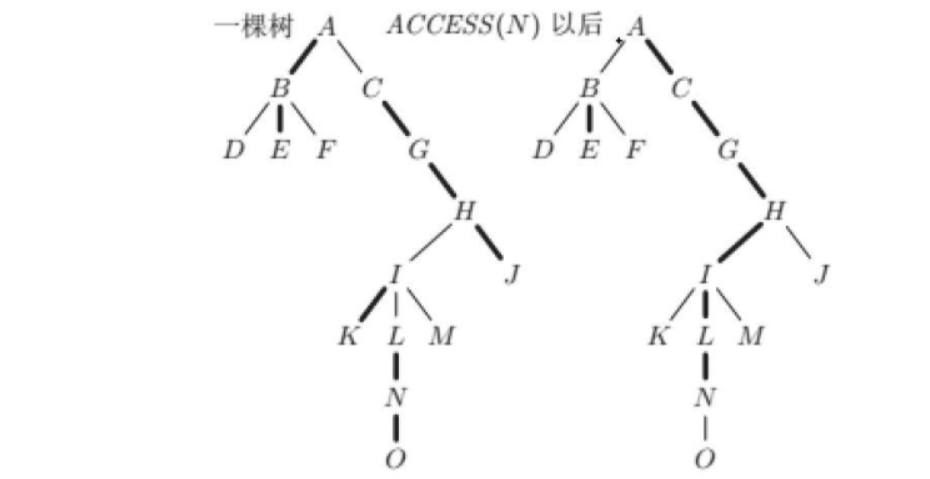
N与根之间可能隔着许多splay,我们需要从N开始不断向上,把N变成所在splay的根,改变N与其父亲之间边的虚实关系,合并splay,由于N上面的点深度小于N,所以N变成父亲的右儿子,同时父亲与原来右儿子之间的边自然变成虚边。
直接看代码:
void access(int x){
for(int y=0;x;){ //y是上一棵树的根节点,初始为0
splay(x); //将当前的点伸展到所属的splay的根节点
spl[x].son[1]=y; //改变虚实
pushup(x);
y=x;
x=spl[x].fa;
}
}
关于LCT的rotate,splay操作与一般伸展树略有不同,下面会将。
makeroot
LCT重要操作,将某个点N变成原树的根,可以理解为对原树的换根,改变原树形态。
首先access(N),这样换根只对N到根这条链上的点有影响。在这条链的splay里,显然N的深度最大,根的深度最小,换根(实际上相当于倒转这条链)后则变成N的深度最小,根的深度最大,于是我们只需要splay(N),然后给N打上区间翻转的懒标记。
void makeroot(int x){
access(x);
splay(x);
swap(spl[x].son[0],spl[x].son[1]);
spl[x].tag^=1;
}
findroot
LCT重要操作,找到原树的根。
也很简单,access(N),然后找到splay里排名为1的点(深度最小)。
int findroot(int x){
access(x);
splay(x);
while(spl[x].son[0]) pushdown(x), x=spl[x].son[0];
splay(x); //保证树的平衡性
return x;
}
split
将原树中两个点之间的路径拉成一条splay
看代码就懂了
void split(int x,int y){
makeroot(x);
access(y);
splay(y);
}
link-cut
有了上面的东西,就可以实现题目所要求的操作啦!
连接两个点:
void link(int x,int y){
makeroot(x);
if(findroot(y)!=x) spl[x].fa=y; //不连通,则连一条虚边
}
断开一条边:
void cut(int x,int y){
makeroot(x);
if(findroot(y)==x&&spl[y].fa==x&&!spl[y].son[0]) //关于第三个,代表x,y间没有其它点
spl[x].son[1]=spl[y].fa=0,pushup(x);
}
关于LCT中的rotate与splay,多了一个判断根的语句,意会意会
bool nroot(int x){
return spl[spl[x].fa].son[0]==x||spl[spl[x].fa].son[1]==x; //判断一个点不是所在splay的根
}
void rotate(int x){
int y=spl[x].fa,z=spl[y].fa;
if(!nroot(x)) return;
int k=(spl[y].son[1]==x);
if(nroot(y)) spl[z].son[spl[z].son[1]==y]=x; //注意
spl[x].fa=z;
spl[y].son[k]=spl[x].son[k^1];
if(spl[x].son[k^1]) spl[spl[x].son[k^1]].fa=y;
spl[x].son[k^1]=y;
spl[y].fa=x;
pushup(y); pushup(x);
}
int stk[maxn];
void splay(int x){
int y=x,z=0;
stk[++z]=y;
while(nroot(y)) stk[++z]=y=spl[y].fa; //用栈从上往下释放懒标记
while(z) pushdown(stk[z--]);
while(nroot(x)){
y=spl[x].fa,z=spl[y].fa;
if(nroot(y))
rotate((spl[y].son[1]==x)^(spl[z].son[1]==y)?x:y);
rotate(x);
}
}
查询
查询的话,把路径拉成一条splay即可。