线性代数的本质,源视频 bilibili
自己一直觉得线性代数没有真的弄懂,对于线性代数的学习基本上都是靠记忆而不是理解,为了认真学习线性代数,弄清线性代数背后的本质,特此学习,做下笔记。
@
什么是向量
线性代数中最基础、最根源的组成部分就是向量,所以对于向量是什么我们需要达成共识然后继续前进。
向量,对于不同领域的人通常对于向量的理解不同,因为在每个领域中的应用和出现的形式有所区别,一般来说有三种不同的理解:
- 在物理学专业看来,向量是空间中带有方向的箭头,而决定一个向量的是它的长度和所指的方向
- 在计算机专业看来,向量是有序的数字列表,例如在房价分析中我们只看房屋面积和价格,那么就会有(房屋面积,价格)这样一个向量
- 在数学专业看来,向量可以是任何东西,只要保证两个向量相加数字与向量相乘是有意义的即可
在这个过程中,向量加法和数字与向量相乘这两种运算是很重要的。
我们考虑这样一个向量,向量是一个
从原点出发的箭头,我们可以分别从物理角度和计算机角度去看待这个向量。
一个向量的坐标由一对数构成,每对数字对应唯一一个向量,每个向量用唯一的一对数字表示。
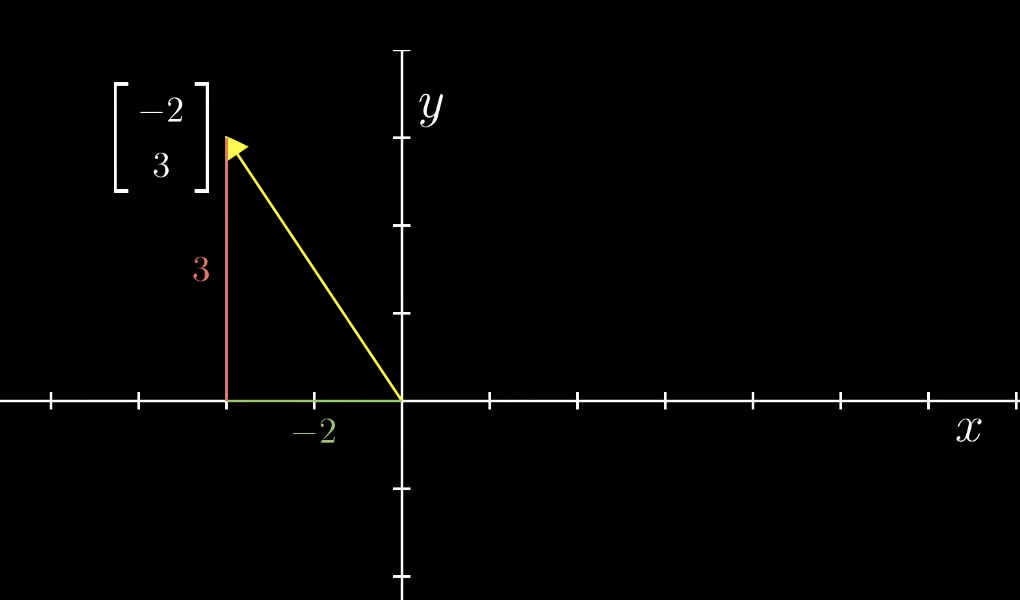
向量加法的定义:
我们可以把向量看作一种运动,即朝着某个方向做一定的运动,而向量的加法就对应于两个向量的运动叠加,如下图。
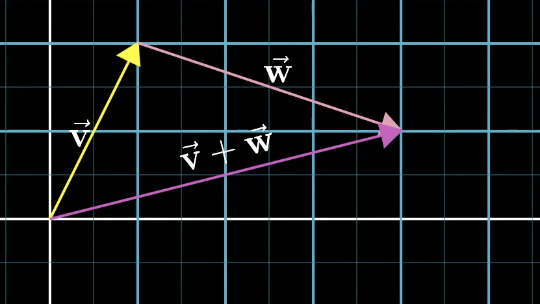
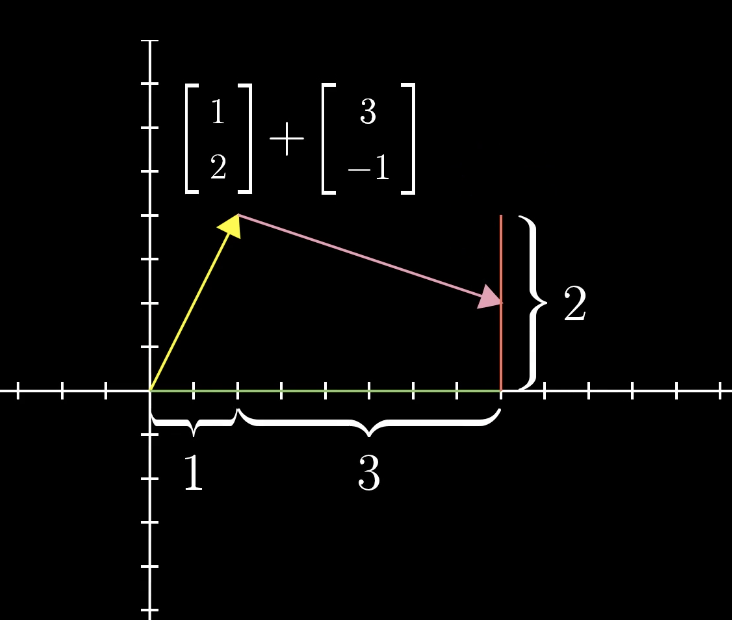
从数字角度看,向量加法就是把对应位置的数字相加。
向量数乘:
在数字与向量做乘法的过程中,没有方向的数字就叫做标量(Scalars),数字起到的主要作用就是缩放向量。

线性变换、张成的空间与基
基的严格定义:
向量空间的一组基是张成该空间的一个线性无关向量集。
线性变换
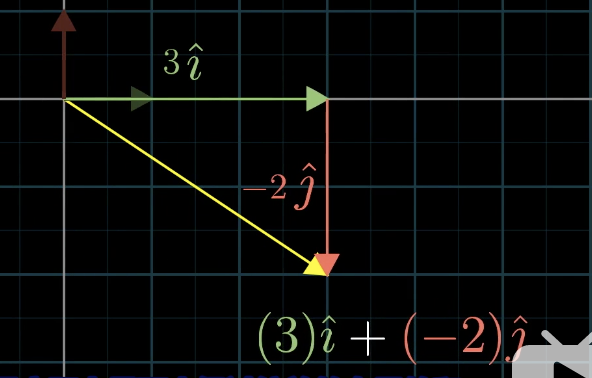
我们都很熟悉坐标了,我们现在用一种新的角度去看待坐标:我们把每个坐标看成标量,他们会放缩某个向量。
而在平面上,有两个特殊的向量,分别为指向正右方的(或者指向x轴正方向)的单位向量 i^,和指向正上方的单位 j^。
我们此时就可以把(3,-2)= 3 * i + (-2) * j 看作是两个经过放缩的向量之和。
记住,缩放向量并且相加这个概念。
此时其实我们把 i 和 j 向量称为 xy 坐标系的基向量。
如果我们选择不同的基向量会怎么样?
答案是选择任何两个向量作为基向量(不共线),我们可以得到平面上所有的向量。
当我们用数字描述一个向量时,它都依赖于我们当前所使用的基向量。
两个向量的和被称为这两个向量的线性组合。
为什么叫线性组合呢?我们提供这样一种思路:
- 当我们让两个向量相加时,如果固定一个向量,让另外一个向量任意移动,所产生向量的终点会描述出一条直线。
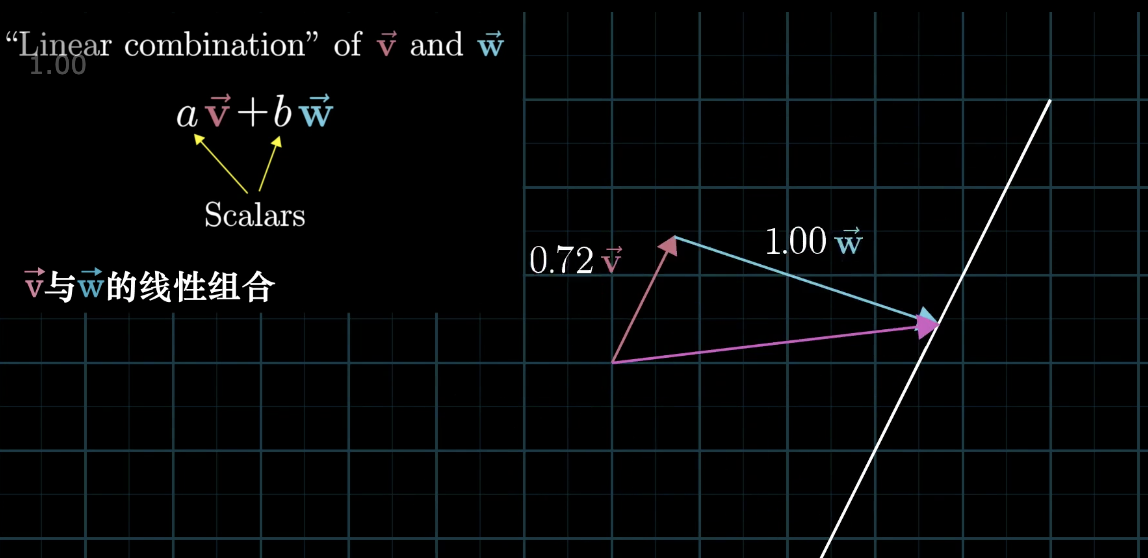
而如果同时变化两个标量,我们就能得到所有的向量!
向量空间
定义:所以可以表示为给定向量线性组合的向量的集合,被称为给定向量张成的空间(span)。
对不共线的任意两个二维向量来说,他们张成的空间是整个二维平面;
而对于共线的两个二维向量来说,他们张成的空间就是一条直线。
其实向量空间所引出的问题就是,仅仅通过向量加法和向量数乘两种操作,你可能得到的所有向量的集合是什么。
向量与点:
当我们考虑很多个向量的时候,通常我们就用向量的终点代表一个向量,因为起点都是原点,当我们考虑所有二维向量时,我们只需要考虑无限大的二维平面即可。
当我们考虑很少的向量的时候,我们还是可以把向量考虑成一个带有箭头的向量。
三维空间张成向量
当我们去考虑三维空间中张成向量的时候,问题变得有趣了。
如果我们固定其中一个向量不动,另外两个向量自由移动,三个向量相加,我们就可以得到一个平面。
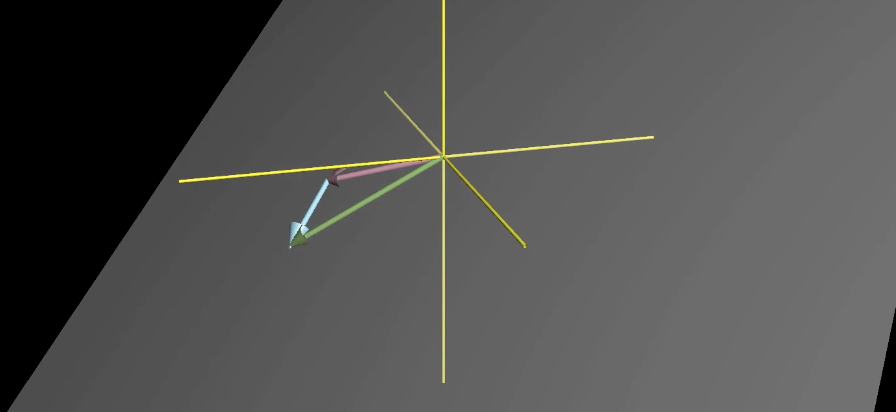
三个向量的线性组合也就是选择三个标量,对三个向量分别进行缩放,然后把结果相加,就得到了三个向量的线性组合。
三个向量所有的线性组合组成了他们张成的空间。
当我们再加上第三个向量的时候,之前两个向量形成的平面沿着第三个向量的方向在空间中移动,直到覆盖了空间中所有的位置(相当于一个面沿着某个方向移动,最终会占满所有的位置)。
多个向量的线性相关
结合之前所说的,我们有两种角度去理解多个向量的线性相关:
- 如果有多个向量,如果移除其中的某一个向量而不会影响他们张成的空间,那么就称这个向量和之前的向量线性相关
- 如果有某一个向量能够被表示成其他向量的线性组合,那么就称这个向量和之前的向量线性相关,因为这个向量已经落在其他向量张成的空间中。
另一方面,如果每个向量都为张成空间作出了贡献,那么就称它们是线性无关的。
之后会继续学习矩阵及其运算和相关性质。