T1
[二分]
期望得分:70
实际得分:10
枚举最高的高度可能为多少+二分。O(logm)
枚举最高高度应该位于哪一列上.O(n)
左右扩散枚举出需要用的积木总数,与m相比较。
容易发现合法的高度的最高值,最终需要搭建一个金字塔。
1,3,5,7…
正解是预处理出每一列作为最高列的左右边界。
然后再二分最大高度。
Check出每个数是否合法即可。
考场做法的错误在于:并不要堆成完全的金字塔形状。
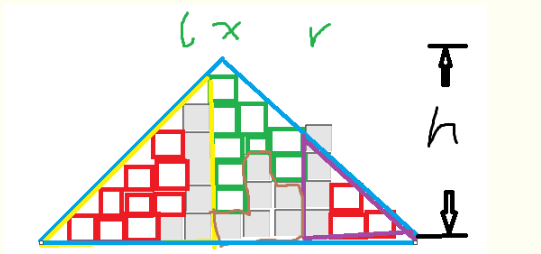
例如上图,其实只需要绿色部分就够了。
居然这么还能苟到10分。。
但是离正解很近了啊啊啊。
【code】

#include<bits/stdc++.h> using namespace std; #define ll long long #define File "block" inline void file(){ freopen(File".in","r",stdin); freopen(File".out","w",stdout); } inline int read(){ int x = 0,f = 1; char ch = getchar(); while(ch < '0' || ch > '9'){if(ch=='-')f = -1; ch = getchar();} while(ch >= '0' && ch <= '9'){x = (x<<1) + (x<<3) + ch-'0'; ch = getchar();} return x*f; } const int mxn = 1e5 + 5; int n,m; int a[mxn]; int L[mxn],R[mxn]; int mx; ll s[mxn]; inline bool check(int h){ int l = n,r = 1; for(int i = n;i >= 1; --i){ while(a[l] < h-(i-l) && l >= 1) l--; L[i] = l; } for(int i = 1;i <= n; ++i){ while(a[r] < h-(r-i) && r <= n) r++; R[i] = r; } for(int i = 1;i <= n; ++i){ ll p,q,t; if(L[i] < 1 || R[i] > n) continue; p = h-(i-L[i]),q = h-(R[i]-i); t = 1ll*h*h-1ll*(p+1)*p/2-1ll*(q+1)*q/2-(s[R[i]-1]-s[L[i]]); if(t <= m) return true; } return false; } int main(){ file(); n = read(),m = read(); for(int i = 1;i <= n; ++i) a[i] = read(),mx = max(mx,a[i]),s[i] = s[i-1]+(ll)a[i]; int l = mx+1,r = (int)(sqrt(m)+1)+mx+1; while(l < r){ int mid = (l+r) >>1; if(check(mid)) l = mid+1; else r = mid; } printf("%d ",l-1); return 0; } /* 8 4 3 4 2 1 3 3 2 4 */ /* 3 100 3 3 3 */
T2
[贪心,链表]
期望得分:30
实际得分:0
知道是个贪心。对于每个n[i],贪心选择较大的前n[i]个m[i]减去1。
正解做法是对贪心进行优化。
正解的链表做法好玄妙好棒哦。
能这么做是因为值域就在[1,m]范围内,而且每次变化就在相邻的两个元素之间。
这样可以用链表快速维护相邻两个数的关系。
据说还有网络流的写法。不想写。我不会。
【code】

#include<bits/stdc++.h> using namespace std; #define ll long long #define File "cake" inline void file(){ freopen(File".in","r",stdin); freopen(File".out","w",stdout); } inline int read(){ int x = 0,f = 1; char ch = getchar(); while(ch < '0' || ch > '9'){if(ch=='-')f = -1; ch = getchar();} while(ch >= '0' && ch <= '9'){x = (x<<1) + (x<<3) + ch-'0'; ch = getchar();} return x*f; } const int mxn = 2.5*1e6 + 19; int m,n,md,nd,m0,n0; inline bool cmp(int x,int y){ return x > y; } int X[mxn],Y[mxn]; int L[mxn],R[mxn]; inline void del(int x){ L[R[x]] = L[x]; R[L[x]] = R[x]; } int main(){ file(); m = read(),n = read(),m0 = read(),md = read(),n0 = read(),nd = read(); X[m0]++,Y[n0]++; for(int i = 1;i < m; ++i) m0 = (m0*58+md)%(n+1),X[m0]++; for(int i = 1;i < n; ++i) n0 = (n0*58+nd)%(m+1),Y[n0]++; for(int i = 1;i < max(n,m)+9; ++i) L[i] = i+1,R[i] = i-1;//从大到小链接 int cur = m,s(0); ll ans(0); for(int i = n; i; --i){ while(X[i] && cur){ --X[i]; while(s < i && R[cur]){ s += Y[cur]; cur = R[cur]; } while(s >= i+Y[cur]){ s -= Y[cur]; cur = L[cur]; } ans += (ll)min(i,s); if(s > i){ int x = Y[cur] - (s-i); if(R[cur]) Y[R[cur]] += x; s -= x; Y[cur] += Y[L[cur]] - x; del(L[cur]); }else{ s -= Y[cur]; if(R[cur]) Y[R[cur]] += Y[cur]; del(cur); cur = L[cur]; } } } printf("%d ",ans); return 0; } /* 5 8 1 2 3 4 */
T3
[树形dp]
可能的得分:30
实际得分:0
暴力就是看图模拟吧。但是没写就是了。
整体总结:
状态不佳。。。不给自己找客观原因吧。
