2020蓝桥杯c++ A组 国赛 皮亚诺曲线距离

2020蓝桥杯c++ A组 皮亚诺曲线距离

时间限制: 1.0s 内存限制: 256.0MB

【问题描述】
皮亚诺曲线是一条平面内的曲线。
下图给出了皮亚诺曲线的 1 阶情形，它是从左下角出发，经过一个 3 × 3 的方格中的每一个格子，最终到达右上角的一条曲线。

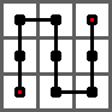
下图给出了皮亚诺曲线的 2 阶情形，它是经过一个 32 × 32 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。

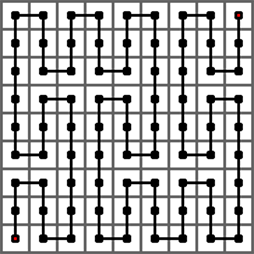
下图给出了皮亚诺曲线的 3 阶情形，它是经过一个 33 × 33 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发，最终到达右上角。

我们将这些格子放到坐标系中，对于 k 阶皮亚诺曲线，左下角的坐标是(0, 0)，右上角坐标是 (3k − 1, 3k − 1)，右下角坐标是 (3k − 1, 0)，左上角坐标是(0, 3k − 1)。

给定 k 阶皮亚诺曲线上的两个点的坐标，请问这两个点之间，如果沿着皮亚诺曲线走，距离是多少？

【输入格式】
输入的第一行包含一个正整数 k，皮亚诺曲线的阶数。第二行包含两个整数 x1, y1，表示第一个点的坐标。
第三行包含两个整数 x2, y2，表示第二个点的坐标。

【输出格式】
输出一个整数，表示给定的两个点之间的距离。

【样例输入】
1
0 0
2 2

【样例输出】
8

【样例输入】
2
0 2
0 3

【样例输出】
13

【评测用例规模与约定】
对于 30% 的评测用例，0 ≤ k ≤ 10。
对于 50% 的评测用例，0 ≤ k ≤ 20。
对于所有评测用例，\(0 ≤ k ≤ 100, 0 ≤ x_1, y_1, x_2, y_2 < 3^k, x_1, y_1, x_2, y_2 ≤ 10^{18}\)。
数据保证答案不超过 \(10^{18}\)。

思路

类似于 分形之城。

对于给定的两个点，我们先求出它们到起点的距离。
差的绝对值就是这两个点的距离和。

递归求解问题。

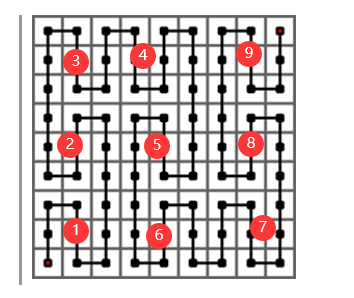
假如现在要求 \((7,4)\) 点到起点的距离。

根据坐标我们可以知道它位于上图中的 \(8\) 部分。

答案转化为了 \(1-7\) 部分中的点的数量+ \((1,1)\) 点在 8 部分中到起点的距离。\((1,1)\) 点是 \((7,4)\) 点在 \(8\) 部分中的坐标。

我们定义一个函数 \(cal(n,x,y) 表示在 n 阶皮亚诺曲线中 (x,y) 到起点的距离\)。

那么我们求出 \((x,y)\) 在 \(id\) 部分之后，可以求出之前的距离：\((id-1) \times (n-1阶曲线的点数)\)，并且得到其在 \(id\) 部分的坐标 \((x',y')\)，将 \(id\) 部分变换成 \(n-1\) 阶皮亚诺曲线（旋转或者翻转），并将 \((x',y')\) 做相应的变换，得到 \((x'',y'')\)。

答案即为 \((id-1) \times (n-1阶曲线的点数) + cal(n-1,x'',y'')\)

递归下去即可。

代码

#include <bits/stdc++.h>
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int mod = 1e9 + 7;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
const int N = 2e5 + 10;

ll fac[N];
ll cal(ll k, ll x, ll y)
{
    if (k == 0)
        return 0;
    ll len = fac[k], cnt = fac[k * 2];
    if (x < len / 3) {
        if (y < len / 3)
            return cal(k - 1, x, y);
        if (y < len * 2 / 3)
            return cnt / 9 + cal(k - 1, len / 3 - x - 1, y - len / 3);
        return cnt / 9 * 2 + cal(k - 1, x, y - 2 * len / 3);
    } else if (x < len * 2 / 3) {
        if (y < len / 3)
            return cnt / 9 * 5 + cal(k - 1, x - len / 3, len / 3 - y - 1);
        if (y < len * 2 / 3)
            return cnt / 9 * 4 + cal(k - 1, x - len / 3, y - len / 3);
        return cnt / 9 * 3 + cal(k - 1, x - len / 3, len - y - 1);
    } else {
        if (y < len / 3)
            return cnt / 9 * 6 + cal(k - 1, x - len * 2 / 3, y);
        if (y < len * 2 / 3)
            return cnt / 9 * 7 + cal(k - 1, len - 1 - x, y - len / 3);
        return cnt / 9 * 8 + cal(k - 1, x - len * 2 / 3, y - len * 2 / 3);
    }
}
int main()
{
    fac[0] = 1;
    for (int i = 1; i <= 100; i++) {
        fac[i] = fac[i - 1] * 3;
    }
    ll k, x1, y1, x2, y2;
    scanf("%lld%lld%lld%lld%lld", &k, &x1, &y1, &x2, &y2);
    ll a = cal(k, x1, y1);
    ll b = cal(k, x2, y2);
    printf("%lld\n", abs(a - b));
    return 0;
}