思路
把左上角的坐标看做 \((0 , 0)\),右上角的坐标为 \((0,2^n-1)\),左下角的坐标为 \((2^n-1,0)\),右下角坐标为 \((2^n-1,2^n-1)\)。
街区的标号也从 \(0\) 开始。
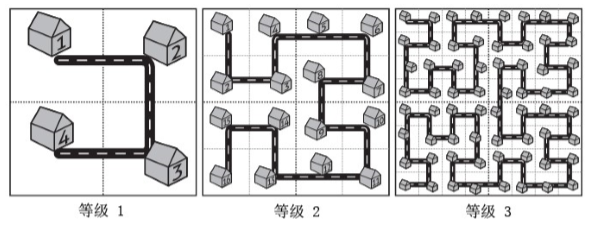
现在对于给定的两个距离,我们要分别求出他们的坐标。

现在给出等级为 \(2\),距离为 \(10\),如何求坐标呢?
等级为 \(1\) 的城市中有 \(4\) 座街区,通过 \(10/4 = 2\),可以知道这个街区在 等级为 \(2\) 的右下角,即图中 \(4\) 部分。
这时如果可以求出它在 \(4\) 中的坐标,横纵坐标都加上 \(2\),就得到了它在等级为 \(2\) 的城市中的坐标。
求其在 \(4\) 中的坐标可以转化为 求在等级 \(1\) 中,距离为 \(10\%4\) 的坐标 (因为 \(4\) 部分是直接复制的等级为 \(1\) 的城市)
这样问题就可以递归解决。
定义函数 \(cal(N,M) 表示求在 N 级城市中,距离起点距离为 M 的坐标\)
求 \(cal(N,M)\) 时,\(N-1\) 级城市有 \(2^{2*N-2}\) 座街区,先递归求解 \(cal(N-1,M mod\ 2^{2*N-2})\)
注意这时还要进行坐标变换:\(4\)部分没有进行是因为它是直接从 \(N-1\) 级城市复制得到的。
假如在 \(1\) 部分,通过观察可以知道,\(1\) 部分是 \(N-1\) 级城市 顺时针旋转,然后水平翻转得到的。
如果在 \(2\) 部分,也不需要变换
如果在 \(3\) 部分,先逆时针旋转90度,然后水平翻转。
如果在 \(4\) 部分,不需要变换。
这时已经得到该点在 \(N-1\) 级城市中的坐标。
那么针对这 \(4\) 部分的点,横纵坐标加上不同的值即可。
\(1\) 部分不需要加
\(2\) 部分纵坐标加上 \(N-1\) 级城市的边长
\(3\) 部分横坐标加上 \(N-1\) 级城市的边长
\(4\) 部分横纵坐标均加上 \(N-1\) 级城市的边长
代码
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int mod = 1e9 + 7;
const double eps = 1e-6;
const int inf = 0x3f3f3f3f;
const int N = 2e5 + 10;
pair<ll, ll> cal(ll n, ll now)
{
if (n == 0)
return { 0, 0 };
ll len = 1LL << (n - 1), cnt = 1LL << (2 * n - 2);
pair<ll, ll> pre = cal(n - 1, now % cnt);
ll x = pre.first, y = pre.second;
int tmp = now / cnt;
if (tmp == 0) {
return { y, x };
} else if (tmp == 1) {
return { x, y + len };
} else if (tmp == 2) {
return { x + len, y + len };
} else {
return { 2 * len - y - 1, len - x - 1 };
}
}
int main()
{
int T;
scanf("%d", &T);
while (T--) {
ll n, a, b;
scanf("%lld%lld%lld", &n, &a, &b);
pair<ll, ll> aga = cal(n, a - 1);
pair<ll, ll> en = cal(n, b - 1);
double dis = sqrt(pow((aga.first - en.first) * 10, 2) + pow((aga.second - en.second) * 10, 2));
printf("%.0lf\n", dis);
}
return 0;
}