10/17 NOIP模拟赛


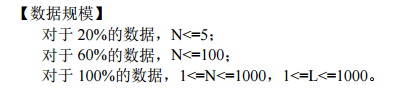
期望得分:50;实际得分:0;
考场思路:暴力(完全没有往贪心的方面想,还差点把ssj带沟里 qwq)
拿到数据发现,这样写暴力完全不对啊。。。。
很多情况没有考虑到 qwq

#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> using namespace std; const int M = 1005; int n, len, sum; int p, q, maxn; char s[M][M]; int main() { // freopen("curse.in","r",stdin); // freopen("curse.out","w",stdout); scanf("%d", &n); for (int i = 1; i <= n; ++i) { cin >> s[i]; len = strlen(s[i]); } for (int i = 1; i <= n; ++i) for (int j = i + 1; j <= n; ++j) { for (int k = 0; k < len; ++k) if (s[i][k] == s[j][k]) ++sum; if (sum > maxn) { maxn = sum; p = i, q = j; } sum = 0; } int y = 0, x = 0; for (int i = 0; i < len; ++i) { if (s[p][i] == '0') ++x; if (s[q][i] == '0') ++y; } if (x > y) cout << s[p] << ' '; else cout << s[q] << ' '; // fclose(stdin); fclose(stdout); return 0; }
正解:贪心,比较每一位上 0、1 出现的次数,若 1 出现次数 > n/2 输出 1,反之输出 0

#include <algorithm> #include <iostream> #include <cstring> #include <cstdio> using namespace std; int n, len; int b[1005]; string s; int main() { scanf("%d", &n); for (int i = 1; i <= n; ++i) { cin >> s; len = s.length(); for (int j = 0; j < len; ++j) { if (s[j] == '1') ++b[j]; } } for (int i = 0; i < len; ++i) if (b[i] > n / 2) printf("1"); else printf("0"); return 0; }


考场思路:二分+?
好像与处理很麻烦的样子。。。不会要用DP吧。。。
然后就放弃了。。。
正解:二分+DP
特判一下,当 R + G ≥ N 时,L = 1 即可全部覆盖,所以DP的范围便从 109 减小到 2 * 103
将祭坛的位置按从小到大排序,然后二分求 L 的大小
预处理 P、Q 两个数组,记录在祭坛 i 使用法杖能摧毁的最远的祭坛
用DP判断二分的 L 是否符合题目要求

#include <algorithm> #include <cstring> #include <cstdio> using namespace std; const int M = 2005; int n, p, q, a[M]; int l = 1, r, ans; int dp[M][M], P[M], Q[M]; bool check(int L) { memset(dp, 0, sizeof dp); memset(P, 0, sizeof P); memset(Q, 0, sizeof Q); for (int i = 1; i <= n; ++i) //预处理 for (int j = i; j <= n; ++j) { if (a[j] - a[i] + 1 <= L) P[i] = j; if (a[j] - a[i] + 1 <= 2 * L) Q[i] = j; } // P[n + 1] = Q[n + 1] = n; 与第25行意义相同,防止DP时超过边界 for (int i = 0; i <= p; ++i) for (int j = 0; j <= q; ++j) { if (i > 0) dp[i][j] = max(dp[i][j], P[dp[i - 1][j] + 1]); if (j > 0) dp[i][j] = max(dp[i][j], Q[dp[i][j - 1] + 1]); if (dp[i][j] == n) return true; } return dp[p][q] == n ? true : false; } int main() { // freopen("light.in", "r", stdin); // freopen("light.out", "w", stdout); scanf("%d%d%d", &n, &p, &q); for (int i = 1; i <= n; ++i) scanf("%d", &a[i]); sort(a + 1, a + 1 + n); a[0] = 0; r = a[n] - a[1] + 1; if (p + q >= n) return printf("1 "), 0; while (l <= r) { //二分 int mid = (l + r) / 2; if (check(mid)) ans = mid, r = mid -1; else l = mid + 1; } printf("%d ", ans); return 0; }


思路:求严格次短路

#include <cassert> #include <cstring> #include <cstdio> #include <queue> using namespace std; #define LOOP(i,n) for(int i=1; i<=n; i++) const int MAX_NODE = 5010; const int MAX_EDGE = 100010 << 1; const int INF = 0x3f3f3f3f; struct Node; struct Edge; struct Node { int Id, Dist, Dist2; bool Inq; Edge *Head; } _nodes[MAX_NODE], *Start, *Target; int _vCount; struct Edge { int Weight; Node *From, *To; Edge *Next; Edge() {} Edge(Node *from, Node *to, Edge *next, int weight) : From(from), To(to), Next(next), Weight(weight) {} }*_edges[MAX_EDGE]; int _eCount; void init(int vCount) { memset(_nodes, 0, sizeof(_nodes)); _vCount = vCount; _eCount = 0; Start = 1 + _nodes; Target = vCount + _nodes; } void AddEdge(Node *from, Node *to, int weight) { Edge *e = _edges[++_eCount] = new Edge(from, to, from->Head, weight); e->From->Head = e; } void Build(int uId, int vId, int weight) { Node *u = uId + _nodes, *v = vId + _nodes; u->Id = uId; v->Id = vId; AddEdge(u, v, weight); AddEdge(v, u, weight); } void SPFA() { LOOP(i, _vCount) _nodes[i].Dist = _nodes[i].Dist2 = INF; static queue<Node*> q; Start->Dist = 0; Start->Dist2 = INF; Start->Inq = true; q.push(Start); while (!q.empty()) { Node *u = q.front(); q.pop(); u->Inq = false; for (Edge *e = u->Head; e; e = e->Next) { bool relaxOk = false; if (u->Dist + e->Weight < e->To->Dist) { e->To->Dist2 = e->To->Dist; e->To->Dist = u->Dist + e->Weight; relaxOk = true; } else if (u->Dist + e->Weight > e->To->Dist && u->Dist + e->Weight < e->To->Dist2) { e->To->Dist2 = u->Dist + e->Weight; relaxOk = true; } if (u->Dist2 + e->Weight < e->To->Dist2) { e->To->Dist2 = u->Dist2 + e->Weight; relaxOk = true; } if (relaxOk && !e->To->Inq) { e->To->Inq = true; q.push(e->To); } } } } int main() { // freopen("maze.in","r",stdin); // freopen("maze.out","w",stdout); int testCase, totNode, totEdge, uId, vId, weight, sId, tId; scanf("%d%d", &totNode, &totEdge); init(totNode); LOOP(i, totEdge) { scanf("%d%d%d", &uId, &vId, &weight); Build(uId, vId, weight); } SPFA(); printf("%d ", Target->Dist2); // fclose(stdin); fclose(stdout); return 0; }
