图论
1.基本概念



2.图的储存

3.路径

4.自由树

5.有根树和二叉树

6.图的遍历

7.连通

8.拓扑排序

9.欧拉路径

10.最短路

(1)Dijkstra

void dijkstra(int x) { for (int i = 1; i <= n; i++) dis[i] = a[x][i]; dis[x] = 1; f[x] = 1; for (int i = 1; i <= n; i++) { minn = 0; for (int j = 1; j <= n; j++) if (f[j] == 0 && dis[j] > minn) { k = j; minn = dis[j]; } f[k] = 1; if (k == y) break; for (int j = 1; j <= n; j++) if(f[j] == 0 && dis[k] * a[k][j] > dis[j]) dis[j] = dis[k] * a[k][j]; } }
(2)Bellman-Ford
不断在最短路中加边
时间复杂度:O(VE)
for (int i = n; i; --i) for (int j = n; j; --j) dis[v[j]] = min(dis[v[j]], dis[u[j]] + w[j]);
(3)Folyd
可以看作DP,同时求出每点对间的最短路
时间复杂度:O(n3)
for (int k = 1; k <= n; ++k) for (int i = 1; i <= n; ++i) for (int j = 1; j <= n; ++j) dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
(4)SPFA
虽然老师没讲,但我平常都写这个。。。
void spfa(int x) { for (int i = 1; i <= n; ++i) dis[i] = MAXN, vis[i] = 0; dis[x] = 0; vis[x] = 1; q.push(x); while (!q.empty()) { int y = q.front(); q.pop(); vis[y] = 0; for (int i = head[y]; i; i = net[i]) { int t = to[i]; if (dis[t] > dis[y] + cap[i]) { dis[t] = dis[y] + cap[i]; if (!vis[t]) vis[t] = 1, q.push(t); } } } }
(5)Johnson重赋权
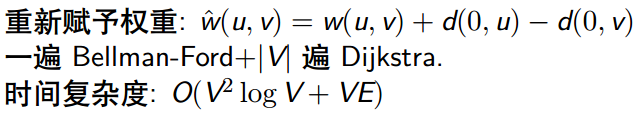
(6)应用:差分约束系统

11.强连通分量

12.边双连通分量

13.点双连通分量

14.最小生成树MST
(1)MST基本定理

(2)MST求解方法

//其他两个不会写qwq //这是kruskal struct nond { int u, v, w; }e[M]; int find(int x) { return fa[x] == x ? x : fa[x] = find(fa[x]); } bool cmp(nond x, nond y) { return x.w < y.w; } void kruskal() { sort(e+1, e+k+1, cmp); for (int i = 1; i <= k; ++i) { int x = find(e[i].u), y = find(e[i].v); if (x == y) continue; fa[x] = y; ++tot; sum += e[i].w; if (tot == n - 1) break; } return ; }
(3)MST的性质

15.最近公共祖先 LCA
(1)定义 给定两点 u 和 v ,lca( u, v ) 即为两点所有公共祖先中深度最深的一个
(2)求法
