二叉搜索树

二叉搜索树

注意：本文的算法和代码思路大部分来自《算法导论》

什么是二叉搜索树

二叉搜索树首先是一棵二叉树，此外，它还能用来搜索。因为它满足这样的性质：每个结点的左子树的结点值都比自身小，而它的右子树的结点值都比自身大。

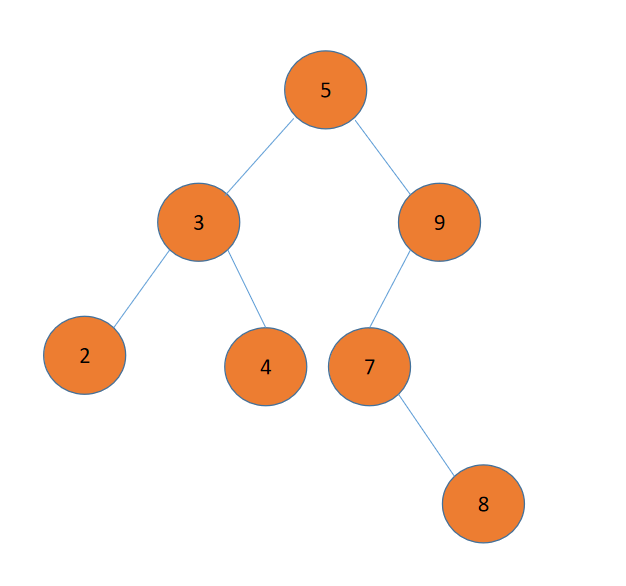
它长得像下面这样：（依据创建时结点插入顺序不同，可能是完全二叉，也可能不是）

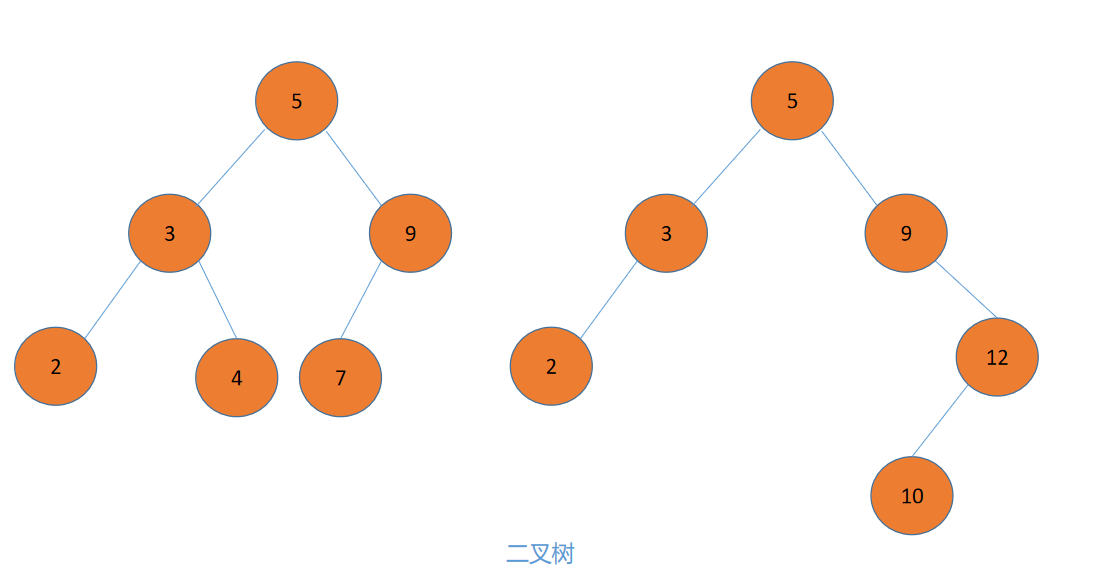
二叉搜索树可以非常方便的用来进行查找指定元素，查找最大值和最小值等。

定义数据结构

我们可以用链表或者数组的方式来实现一棵树。这里我们采用链表的方式。

首先定义节点结构，可以看到，每个结点有一个值，并且有两个孩子，并且有一个父亲。

此外，我们还要额外定义一棵树的结构，它很简单，只有一个指向树根的指针。

//树结点结构
struct Node {
	int key;
	Node* left;
	Node* right;
	Node* parent;
};

//树
struct Tree {
	Node* root;
};

二叉树的遍历

因为二叉搜索树的特殊性质，我们对其进行中序遍历就可以得到所有元素的一个有序序列。

遍历既可以用递归也可以用迭代的方式去实现，这里给出递归的版本：

//中序遍历
void inorder_tree_walk(Node* x) {
	if (x != NULL) {
		inorder_tree_walk(x->left);
		cout << x->key << " ";
		inorder_tree_walk(x->right);
	}
}
//前序遍历
void preorder_tree_walk(Node* x) {
	if (x != NULL) {
		cout << x->key << " ";
		preorder_tree_walk(x->left);
		preorder_tree_walk(x->right);
	}
}
//后续遍历
void postorder_tree_walk(Node* x) {
	if (x != NULL) {
		postorder_tree_walk(x->left);
		postorder_tree_walk(x->right);
		cout << x->key << " ";
	}
}

遍历二叉树的时间复杂度是：O(n)。

如对上图左边的那棵树进行中序遍历的话，得到的序列就是：2 3 4 5 7 9

查询指定结点值

如果给出一个关键字，想要查询其是否存在与二叉树中，如果存在则返回指向它的结点的指针。这个过程可以描述如下：首先把关键字和根结点的值做比较，如果相等则返回；否则，如果比根节点值小，那就递归的在左子树中查找，否则就在右子树中查找。

这个过程既可以用递归去实现，也可以用迭代去实现，这里给出两个版本：

//递归版
Node* tree_search(Node* x, int k) {
	//找到或者为空
	if (x == NULL || k == x->key) {
		return x;
	}
	if (k < x->key) {
		return tree_search(x->left, k);
	}
	else {
		return tree_search(x->right, k);
	}
}

//迭代版
Node* iterative_tree_search(Node* x, int k) {
	while (x != NULL && k != x->key) {
		if (k < x->key) {
			x = x->left;
		}
		else {
			x = x->right;
		}
	}
	return x;
}

最大元素和最小元素

根据二叉搜索树的性质，左子树的结点值都比其父节点的小，而右子树的相反。所以，只要从树根开始，沿着左孩子进行查找，直到最后一个左孩子，那它肯定就是最小值。最大值也是类似。

像这里：

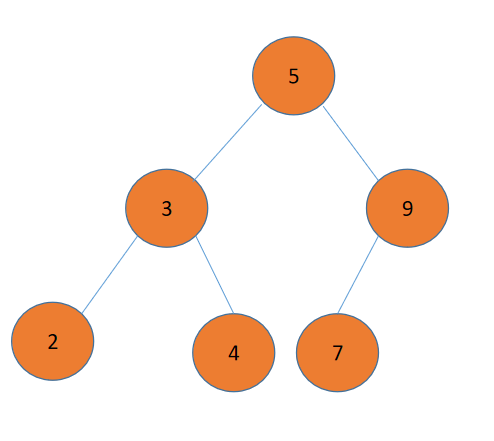
这里给出迭代方式的实现：

//找最小结点
Node* tree_minimum(Node* x) {
	while (x->left != NULL) {
		x = x->left;
	}
	return x;
}
//找最大结点
Node* tree_maximum(Node* x) {
	while (x->right != NULL) {
		x = x->right;
	}
	return x;
}

前驱和后继

一个结点的前驱和后继是什么呢？它是按照中序遍历时，排在该结点前和后的第一个结点。

如：上图的中序遍历是：2 3 4 5 7 9 ， 那5的前驱就是4，而其后继就是7。

也就是，前驱是刚好比它小（或者等于）的元素，后继是刚好比它大（或者等于）的元素。

那要怎么找呢？

首先看这幅图：

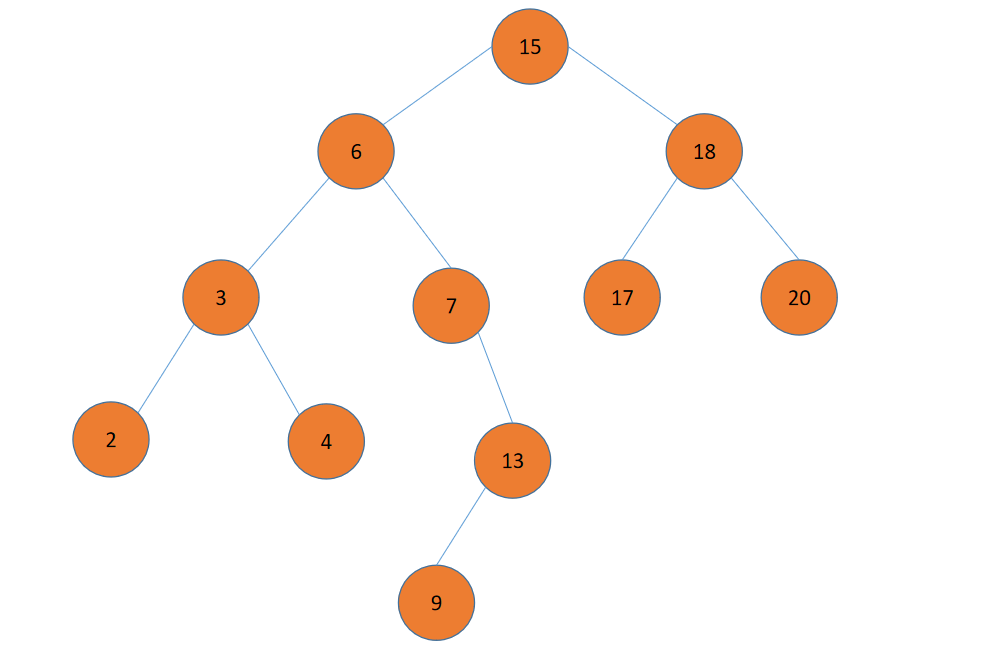
我们先讨论，有左子树的结点的前驱，和有右子树的结点的后继。

首先，有左子树的结点的前驱。我们知道，一个节点的左子树的值都比他自身小，所以它的前驱肯定是在左子树中，而且是左子树中最大的那一个。比如说，结点6，它的前驱就是左子树中最大的那个，也就是4。

然后，是有右子树的结点的后继。很显然，它应该是它的右子树中最小的那。比如说，结点

6，它的后继就是右子树中最小的那个，也就是7。

那么，为什么有左子树的前驱一定在左子树中，而不可能在它的父系结点或其他地方呢？

我们可以这样考虑，看到结点13，它有一个左子树，左子树的结点值都比它小。它有一个父亲7，且它是它父亲的右孩子，所以父亲也比它小。那有没有可能，父亲的某一个取值会使得它是13的前驱呢？答案是不可能的。因为前驱是比它小之中的最大的那个，而如果它有左子树，那左子树中的元素因为在它13的父亲结点的右子树中，所以肯定比父亲结点7要大，但是却比13小。

接下来是，没有左子树的结点的前驱，和没有右子树的结点的后继。

显然，没有左子树的结点的前驱不可能在左子树里找，只能在其他地方找。注意到，前驱和后继其实是对称的关系，如果b的前驱是a，那么a的后继肯定就是b。所以我们要找到a的后继，相当于要找到b的前驱。比如说我们要找到结点7的前驱，那如果能找到某个结点，它的后继是7，那就完事了。因为7没有左子树，所以7的前驱肯定在父亲结点上面。而因为6的后继就是7，所以6就是7的前驱（可以这样验证，因为6有右子树，且7是右子树中最小的那个，所以7是6的后继）。所以这个前驱节点a满足这样一个性质：它肯定在结点b的父系结点上，并且，它是第一个使得b在它的右子树中的结点。

相应的，没有右子树的结点的后继也是类似求法。

这里给出实现方法：

//前驱
Node* tree_predecessor(Node* x) {
	//如果左子树非空，则前驱是左子树中最大的结点
	if (x->left != NULL) {
		return tree_maximum(x->left);
	}
	//否则，找到父系结点中第一个使得它是其右子孙的结点
	Node* y = x->parent;
	while (y != NULL && y->left == x) {
		x = y;
		y = x->parent;
	}
	return y;
}

//后继
Node* tree_successor(Node* x) {
	//如果右子树非空，则后继是右子树中的最左结点
	if (x->right != NULL) {
		return tree_minimum(x->right);
	}
	//否则，找到父系结点中第一个使得它是其左子孙的结点
	Node* y = x->parent;
	while (y != NULL && y->right == x) {
		x = y;
		y = x->parent;
	}
	return y;
}

插入

首先，要明确一点，新结点肯定是以叶节点的形式插入的。而我们要找的就是那个能收养它的父结点。

比如说，我们要在这棵树里插入结点8：

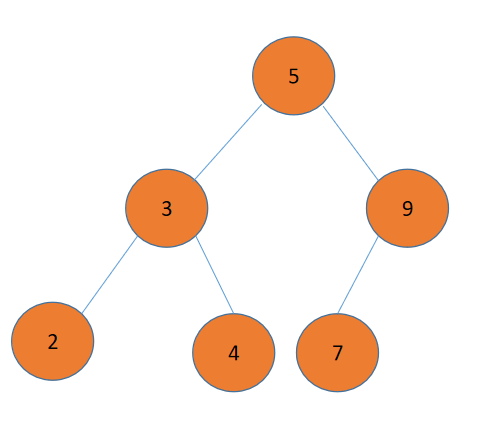
首先，8和5比较，比5大，在右子树中查找。然后和9比较，比9小；最后和7比较，比7大，但因为7已经没有右子树了，所以就把8挂在7的右子树上。

实现如下：

void tree_insert(Tree* T, Node* z) {
	Node* y = NULL;  //用来记住父节点
	Node* x = T->root;   //从根开始查找
	while (x != NULL) {
		y = x;   //记住要挂留的父节点
		if (z->key < x->key) {   //在左子树中找
			x = x->left;
		}
		else {
			x = x->right;    //在右子树中找
		}
	}
	z->parent = y;  //挂上去
	if (y == NULL) {   //如果树是空的
		T->root = z;
	}
	//父亲收养它
	else if (z->key < y->key) {
		y->left = z;
	}
	else {
		y->right = z;
	}
}

删除

删除是一件比较麻烦的事。我们分3种大的情况来讨论。

• 如果z没有孩子结点，那么只是简单的把它删除掉，并且修改它的父节点指向空。

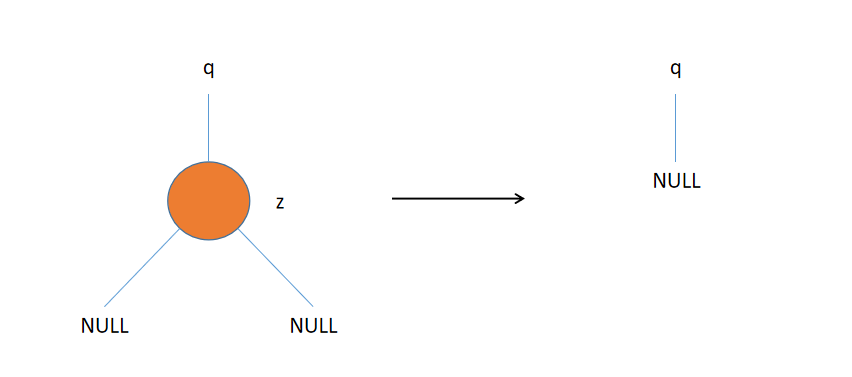
• 如果z只有一个孩子，那么将这个孩子提升到树中z的位置上，并修改z的父节点的孩子指针。

  

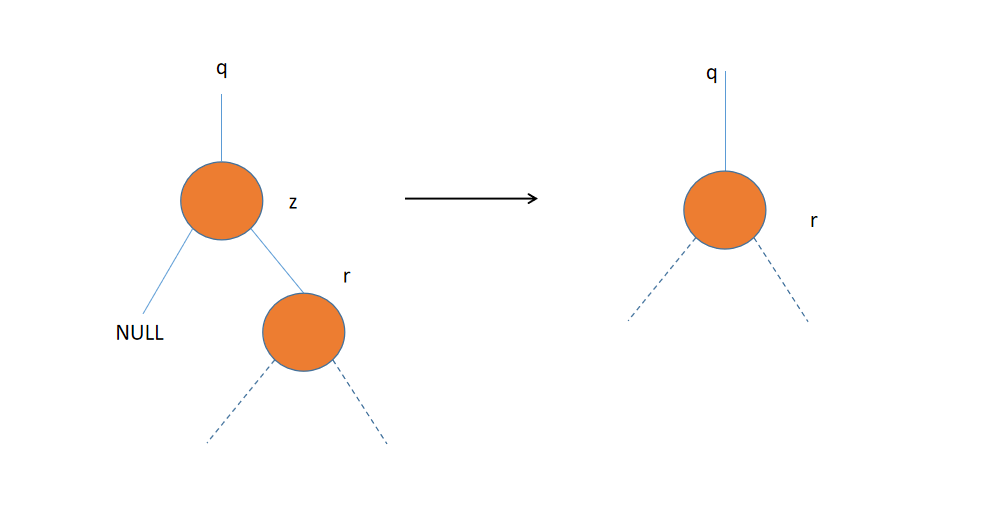
• 如果z有两个孩子，那么找到z的后继y（在右子树中），并让y占据z的位置。

  这里有细分为两种情况：

  • 如果y是z的右孩子，则直接把以y为根的子树放到z上，在让z的左子树成为y的左子树。

    

  • 如果y不是z的右孩子，则先用y的右孩子来替换y，在用y替换z。

  

  为了完成以上工作，额外定义一个函数transplant，它专门用来移植结点。它用一棵以v为根的子树来替换一棵以u为根的子树，结点u的双亲变为结点v的双亲，并且最后v成为u的双亲的相应孩子。

  代码如下：

  void transplant(Tree* T, Node* u, Node* v) {
  	if (u->parent == NULL) {   //如果被替换的是树根，则要让其成为树根
  		T->root = v;
  	}
  	else if (u == u->parent->left) {   //如果被替换的那个结点是其父节点的左孩子
  		u->parent->left = v;
  	}
  	else {                         //否则是右孩子
  		u->parent->right = v;
  	}
  	if (v != NULL) {         //指向父节点
  		v->parent = u->parent;
  	}
  }
  
  void tree_delete(Tree* T, Node* z) {
  	//对应第一种和第二种情况
  	if (z->left == NULL) {          
  		transplant(T, z, z->right);
  	}
  	else if (z->right == NULL) {     
  		transplant(T, z, z->left);
  	}
  	//对应第三种情况
  	else {
  		Node* y = tree_minimum(z->right);
  		if (y->parent != z) { //如果y不是z的直接右孩子
  			transplant(T, y, y->right);
  			y->right = z->right;
  			y->right->parent = y;
  		}
  		transplant(T, z, y);
  		y->left = z->left;
  		y->left->parent = y;
  	}
  }
  

参考资料: 《算法导论》Thomas H. Cormen Charles E.Leiserson && Ronald L.Rivest Clifford Stein 著