线段树

一直没写关于线段树的题解，简单的补两个部分。完整的请转https://blog.csdn.net/yrhsilence/article/details/5793699

线段树做了很多，感觉这类题其实比别的算法更简单，只不过代码量比较大。

关于树，大家明白一点就行

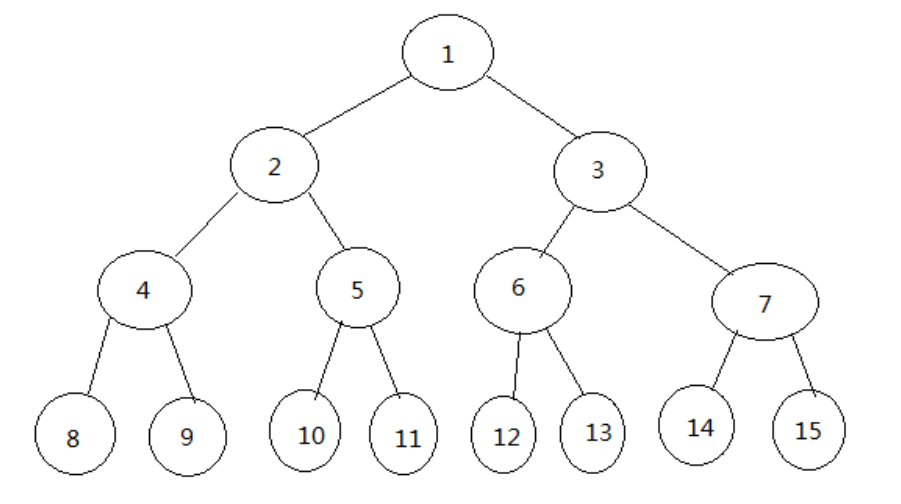
　　　　　　                          父节点 n

                                     ——                ——

                              父节点*2                      父节点*2+1

即                           n*2                              n*2+1

二进制中                左移1位                        左移1位+1

下面，我简单说两类，一个是区间求和，一个是区间求最值

1.hdu1166 敌兵布阵  

#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#include <string.h>
#include <string>
#include <algorithm>
#include <iostream>
#include <ctype.h>
#include <set>
#include <map>
#include <vector>
#include <stack>
#include <queue>
#define left (now<<1)
#define right ((now<<1)+1)
#define mid ((l+r)>>1)
#define fst first
#define snd second
using namespace std;
typedef long long lint;

struct segmentTree{
    int sum;
};

int t,n,a[50010];
char str[10];
segmentTree tree[2000010];

void buildTree(int now,int l,int r){   //建树
    if(l == r){
        tree[now].sum = a[l]; return;
    }
    buildTree(left,l,mid); buildTree(right,mid+1,r);
    tree[now].sum = tree[left].sum + tree[right].sum;
    return;
}

void updateTree(int now,int l,int r,int set,int setNum){  //更新树
    if(l == r){
        tree[now].sum += setNum;
        return;
    }
    if(set <= mid){
        updateTree(left,l,mid,set,setNum);
    }else{
        updateTree(right,mid+1,r,set,setNum);
    }
    tree[now].sum = tree[left].sum + tree[right].sum;
}

int getSum(int now,int l,int r,int ql,int qr){   //求和
   if(ql == l && qr == r){
       return tree[now].sum;
   } 
   int re = 0;
   if(ql <= mid){
       re += getSum(left,l,mid,ql,min(qr,mid));
   }
   
   if(qr > mid){
       re += getSum(right,mid+1,r,max(ql,mid+1),qr);
   }
   return re;
}

int main(){
    scanf("%d",&t);
    int ca = 0;
    while(t--){
        ++ca;
        memset(a,0,sizeof(a));
        scanf("%d",&n);
        for(int i = 1; i <= n; ++i){
            scanf("%d",&a[i]);
        }
        scanf("%s",str);
        buildTree(1,1,n);
        printf("Case %d:n",ca);
        while(str[0] != 'E'){
            if(str[0] == 'A'){
                int u,v;
                scanf("%d%d",&u,&v);
                updateTree(1,1,n,u,v);
            }else if(str[0] == 'S'){
                int u,v;
                scanf("%d%d",&u,&v);
                updateTree(1,1,n,u,-v);
            }else if(str[0] == 'Q'){
                int u,v;
                scanf("%d%d",&u,&v);
                int ans = getSum(1,1,n,u,v);
                printf("%dn",ans);
            }
            scanf("%s",str);
        }
    }
}

（其实有一种后缀数组做这个题更好，这里主要是为了练一下线段树，树状数组可以放一放）

#include"stdio.h"
#include"string.h"
long long lqq[50005];
int n;
int lowbit(int x)
{
    return x&(-x);
}
void insert(int i,int k)
{
    while(i<=n)
    {
        lqq[i]+=k;
        i+=lowbit(i);
    }
}
long long getsum(int n)
{
    long long sum=0;
    while(n)
    {
        sum+=lqq[n];
        n-=lowbit(n);
    }
    return sum;
} 
int main()
{
    int t,i,k,T=1;
    char s[10];
    scanf("%d",&t);
    while(t--)
    {
        printf("Case %d:
",T++);
        memset(lqq,0,sizeof(lqq));
        scanf("%d",&n);
        for(i=1;i<=n;i++)
        {
            scanf("%d",&k);
            insert(i,k);
        }
        scanf("%s",s);
        while(strcmp(s,"End"))
        {
            scanf("%d%d",&i,&k);
            if(strcmp(s,"Add")==0)
            insert(i,k);
            else if(strcmp(s,"Sub")==0)
            insert(i,-k);
            else printf("%d
",getsum(k)-getsum(i-1));
            scanf("%s",s);
        }
    }
    return 0;
}

2.hdu1754 I Hate It

这个题真的很有意思，而且跟2017年acm区域赛网络资格赛的一个题超级像！！！务必好好看一下

#include<iostream>
#include<cmath>
#include<cstdio>

//hduoj 1754  G++


const int  MAXN = 800000;
using namespace std;

struct node
{
    int left,right,value;
} node[MAXN];
int father[MAXN];

int MAX(int x,int y)
{
    return x>=y ? x:y;
}

//建树
void Build(int i, int left,int right)
{
    node[i].left = left ;
    node[i].right = right ;
    node[i].value = 0;
    if(left == right)
    {
        father[left] = i;
        return ;
    }
    Build((i << 1) , left, (int)( floor(left + right) / 2.0 ));
    Build((i << 1)+1 , (int)( floor(left + right)/2.0)+1 , right );
}


//更新
void Update(int ri)
{
    if( ri == 1)
        return ;
    int fi = ri / 2 ;
    int a,b;
    a = node[fi<<1].value;
    b = node[ (fi<<1) +1].value;
    node[fi].value = MAX(a,b);
    Update(ri / 2) ;
}


//查询
int Max;
void Query(int i, int l, int r)
{
    if(node[i].left == l && node[i].right == r )
    {
        Max = MAX(Max, node[i].value );
        return ;
    }
    i = i << 1 ;
    if( l <= node[i].right )
    {
        if(r <= node[i].right)
            Query(i, l, r );
        else
            Query(i, l, node[i].right );
    }
    i++;
    if( r>= node[i].left )
    {
        if( l >= node[i]. left )
            Query(i, l, r );
        else
            Query( i, node[i].left, r);
    }
}


//主函数
int main()
{
    int n,m,g;
    while(scanf("%d%d", &n,&m )!=EOF)
    {
        Build( 1, 1, n );
        for(int i = 1 ; i <= n ; i++ )
        {
            scanf("%d", &g );
            node[father[i]].value = g;
            Update(father[i]);
        }
        string op;
        int a,b;
        while(m--)
        {
            cin>>op>>a>>b;
            if(op[0] == 'Q')
            {
                Max = 0;
                Query(1,a,b);
                cout<<Max<<endl;
            }
            else
            {
                node[father[a]].value  = b;
                Update(father[a]);
            }
        }
    }
}
/*5 6
1 2 3 4 5
Q 1 5
U 3 6
Q 3 4
Q 4 5
U 2 9
Q 1 5

5  6  5  9*/