1，什么是LCA
LCA。最近公共祖先。是一个在解决树上问题最强劲有力的一个工具。一般都是指。在一棵树上取两个节点a,b 。另一个节点x它满足 x是a与b的祖先而且x深度最大。这个x就是节点a,b的最近公共祖先。
2，什么是树上倍增。
树上倍增。其实就是通过二进制拆分。将规则一定情况下加速区间状态转移，的一种奇技淫巧。实质是根据已经得到的信息，将考虑的范围扩大一倍，从而加速操作的思想。 其实就是预处理出一个表。每次通过翻倍区间去查询。 >往下看<可能会更清楚。毕竟实践是检验真理的唯一标准。
3，How to 实现它
首先，来一棵树。
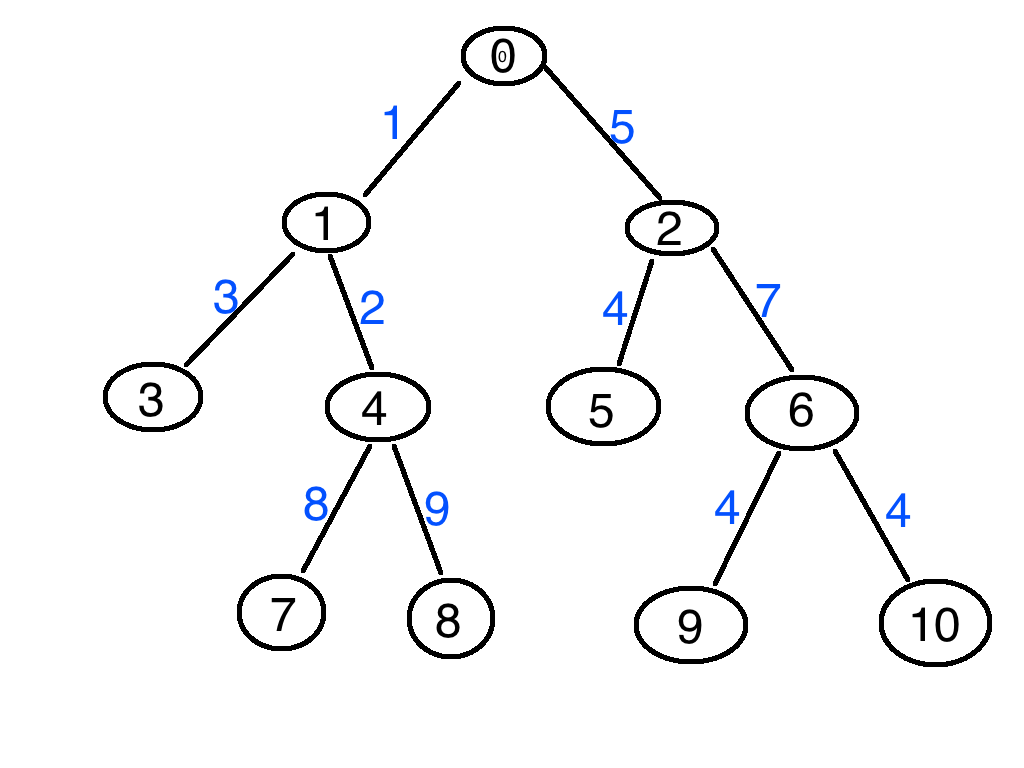其次 我们有一个数组来存，一个节点第几个祖先是谁。
二维：F[i][j] 其中j代表子节点。i代表j这个节点第2^i个祖先。
所以我们要做的就是预处理。将 j节点每第2^i个祖先先存起来。之后就是倍增查询就好。而这里的i其实没有限度。但是一般情况下，20就够用了。2^20就已经够大了。也不能再大不过也没必要。
for(int i=1;i<=n;++i)f[0][i]=father[i];//这里可以在建边的时候操作。
for(int i=1;i<=20;++i)
for(int j=1;j<=n;++j)
f[i][j]=f[i-1][f[i-1][j]];//关键转移。
关注这里f[i][j]=f[i-1][f[i-1][j]];这里f[i-1][j]指的是上一个2^(i-1)的祖先的位置。而我们又要查询这个祖先节点的2^(i-1)其实就是翻了一倍(准确说不是一倍，感性上可以这么认知) 举个栗子。我们这里要找10号节点2^1的祖先的位置。而我们先找10第2^(1-1)祖先的位置 也就是 6号节点。之后再找6号节点2^(1-1)的位置也就是 2号节点。而我们这里找到的2号节点也就是 10号节点第2^1个祖先的位置。
而第一行的处理是节点父亲的处理。这个可以放到建边的时候进行，就不需要用储存并查集，浪费的很。
这里预处理好等着我们的就是查询了。
还是这张图。任意取两个点 8号节点和6号节点。我们查询这两个点的LCA。
1，判断深度。如果深度不同。得把深度大的点跳转到同一深度。（因为接下来要同时跳转所以得达到相同起点）。而这里跳每次当遇到祖先的深度比小深度的节点，
2，迷之审判。如果2个节点刚好在同一个链上而且，1个刚好是另一个祖先。那我们跳完之后还得判断一下跳完之后的节点和另一个节点是不是相同。
3，同时跳转。每次去寻找它们第2^i个祖先（从大往小找）。如果都相同说明 嗯～都相同可能是他们祖先的祖先的祖先的祖先。但是一旦出现不相同的说明。可能离最近公共祖先可能更近了。就跳到当前节点去，继续重复这一条，直到他们的父亲是相同的。那说明，此时，他们的父亲，就是初始的2个点的最近公共祖先。
int LCA(int x,int y)
{
if(dep[x]>dep[y])swap(x,y); //步骤1
for(int i=20;~i;--i) //注释1
{
if(dep[f[i][y]]>=dep[x])
{
y=f[i][y];
}
}
if(y==x)return x; //步骤2
for(int i=20;~i;--i) //步骤3
{
if(f[i][x]!=f[i][y]) //注释2
{
x=f[i][x];
y=f[i][y];
}
}
return f[0][x];
}
注释1：我们会发现。为什么这里就只有一层循环，而我们每次跳都要继续往上跳。每次上一次跳的节点2^i步都没有跳过，当2^(i-1)时跳过去。之后跳的步数也不可能再大于2^(i-1)所以这里只有一层循环。每次都在逼近答案。如果深度相同，或者小于。那么就可以跳。反正当都相同了。下面的循环做其实也都没意义了。
注释2:我们发现这里如果f[i][x]==f[i][y]的情况出现，那么就有两种事情发生。1，是他们的祖先的祖先的祖先....2，是他们的LCA。但是显然我们没法分辨这个东西。所以我们要在不相同的时候跳转，每次都在逼近答案。而我们达到他们两个节点的父亲相同了，那么就找到LCA了。只有一层循环的原因同上。所以最后返回的也是他的父亲。
这就是找LCA的倍增的方法。这个方法是我最先掌握的。。其实也不是很难。。
4，来道题强化一下
codevs 2370 小机房的树
时间限制: 1 s
空间限制: 256000 KB
题目等级 : 钻石 Diamond
题目描述 Description
小机房有棵焕狗种的树，树上有N个节点，节点标号为0到N-1，有两只虫子名叫飘狗和大吉狗，分居在两个不同的节点上。有一天，他们想爬到一个节点上去搞基，但是作为两只虫子，他们不想花费太多精力。已知从某个节点爬到其父亲节点要花费 c 的能量（从父亲节点爬到此节点也相同），他们想找出一条花费精力最短的路，以使得搞基的时候精力旺盛，他们找到你要你设计一个程序来找到这条路，要求你告诉他们最少需要花费多少精力
输入描述 Input Description
第一行一个n，接下来n-1行每一行有三个整数u，v, c 。表示节点 u 爬到节点 v 需要花费 c 的精力。
第n+1行有一个整数m表示有m次询问。接下来m行每一行有两个整数 u ，v 表示两只虫子所在的节点
输出描述 Output Description
一共有m行，每一行一个整数，表示对于该次询问所得出的最短距离。
样例输入 Sample Input
3
1 0 1
2 0 1
3
1 0
2 0
1 2
样例输出 Sample Output
1
1
2
数据范围及提示 Data Size & Hint
1<=n<=50000， 1<=m<=75000， 0<=c<=1000
分析：这道题，有点裸。首先求出两点的LCA，之后无论在什么情况下跳转点的时候都要纪录长度。注意建树的时候方向。这个小细节要注意好。还有。不要搞基。搞gay对身体不好。。虽然1句话题解感觉很不负责任。但是。没什么要讲的了吧。。。。
#include<algorithm>
#include<cstdio>
#include<string.h>
using namespace std;
struct node{
int val,mean;
}f[21][500100];
int n,m,c;
int head[500010],cnt;
int dep[500010];
struct node_1{
int v,next,val;
}edge[100010];
void add(int x,int y,int val)
{
edge[++cnt].v=y;
edge[cnt].next=head[x];
edge[cnt].val=val;
head[x]=cnt;
edge[++cnt].v=x;
edge[cnt].next=head[y];
edge[cnt].val=val;
head[y]=cnt;
f[0][x].mean=y;
f[0][x].val=val;
return ;
}
int visit[100010];
void DFS(int x,int step)
{
visit[x]=1;
dep[x]=step;
for(int i=head[x];i!=-1;i=edge[i].next)
{
if(visit[edge[i].v])continue;
DFS(edge[i].v,step+1);
}
return ;
}
long long int LCA(int x,int y)
{
long long int ans=0;
if(dep[x]>dep[y])swap(x,y);
for(int i=20;~i;--i)
{
if(dep[f[i][y].mean]>=dep[x])//不要忘了这的等号
{
ans+=f[i][y].val;
y=f[i][y].mean;
}
}
if(x==y)return ans;
for(int i=20;~i;--i)
{
if(f[i][x].mean!=f[i][y].mean)
{
ans=f[i][x].val+f[i][y].val+ans;
x=f[i][x].mean;
y=f[i][y].mean;
}
}
ans=ans+f[0][x].val+f[0][y].val;
return ans;
}
int main()
{
memset(head,-1,sizeof(head));
scanf("%d",&n);
for(int i=0;i<n;++i)dep[i]=1;
int x,y,z;
for(int i=1;i<n;++i)
{
scanf("%d%d%d",&x,&y,&z);
add(y,x,z);
}
DFS(0,1);//对深度的处理
f[0][0].val=0;f[0][0].mean=0;
for(int i=1;i<=20;++i)
for(int j=0;j<n;++j)
{
f[i][j].val=f[i-1][j].val+f[i-1][f[i-1][j].mean].val;
f[i][j].mean=f[i-1][f[i-1][j].mean].mean;
}
int a,b,q;
scanf("%d",&q);
for(int i=1;i<=q;++i)
{
scanf("%d%d",&a,&b);
printf("%lld
",LCA(a,b));//不开longlong见祖宗，十年OI一场空。
}
return 0;
}
嗯。就是这样