第一段
import java.util.Arrays;
/**
* 查阅:
* https://blog.csdn.net/m0_52711790/article/details/123012899
* https://baike.baidu.com/item/%E7%A9%BA%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6/9664257?fr=aladdin
*/
public class SwapArrayTest {
/**
* 今天有位面试官问了一个常见的小算法题
* 有个数组大小10,需要将整个数组元素进行倒置
* 那么我感觉应该是这样来解决的
*/
public static void main(String[] args) {
int[] arr = {1,2,3,4,5,6,7,8,9,10,11};
for(int i=0;i<arr.length/2;i++){
swap(i,arr.length-1-i,arr);
}
Arrays.stream(arr).forEach(System.out::println);
/**
* 虽然每个元素都进行来移动,但是是在原数组空间上进行交换
* 所以是原地排序
* 如果数组大小为偶数,其中中间都元素是不用动的
* 所以从算法时间复杂度上来讲是O(n/2)
* 从空间复杂度上来讲,因为只是作为两两交换
* 并没有开辟新的内存空间
* 而交换是声明的int temp
* 可以说每次n/2的数据过来作为一个缓存
* 但是每次都只是赋值给temp并没有temp2
* 那么空间复杂度也为O(1))
*/
}
/**
* swap the array's element
* @param aIndex left nearly element index
* @param bIndex right nearly element index
* @param arr original array
*/
public static void swap(int aIndex,int bIndex,int[] arr){
int temp = arr[aIndex];
arr[aIndex] = arr[bIndex];
arr[bIndex] = temp;
}
}
第二段
import java.util.Arrays;
public class SwapArrayMethod2Test {
public static void main(String[] args) {
int[] arr = {1,2,3,4,5,6,7,8,9,10};
int [] arrResult = new int[arr.length];
/**
* 这样都做法虽然不用进行交换了
* 但是需要声明一个同样大小都数组
* 从而不是原地算法了
* 是完全借助了另一个数组
* 不过从实现上也更加好理解
* 其空间复杂度为O(n)
* 时间复杂度为O(n)
* 会创建n大小都数组
* 也会将数据一个一个遍历一遍
*/
for(int i=0;i<arr.length;i++){
arrResult[i]=arr[arr.length-1-i];
}
Arrays.stream(arrResult).forEach(System.out::println);
}
}
此时我设定一个大的数组
public class TheArrays {
public static int[] arr;
static{
arr=new int[100000000];
for(int i=1;i<=100000000;i++){
arr[i-1]=i;
}
}
}
当不是1E,而是1000W的数据时,相差的时间几乎感觉不到差异。
但一旦像如上数组,到了1E的数据量,算法的时间就完全不同了。
第一段逆序的花费时间大概在36~50ms(毫秒)
而第二段则花费了202~400ms之间
并且开辟一个1E大小的数组空间真是个不小的消费
再通过VisualVM来看一下两个算法各自占用的堆空间
交换的:
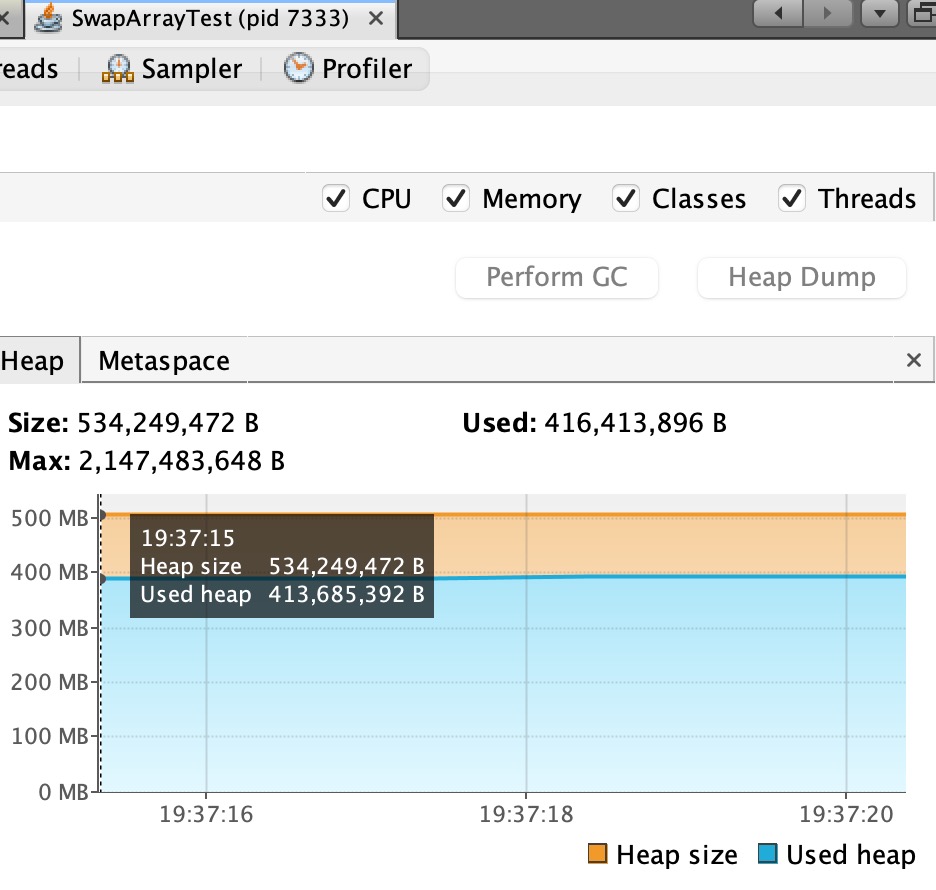
开辟数组的:
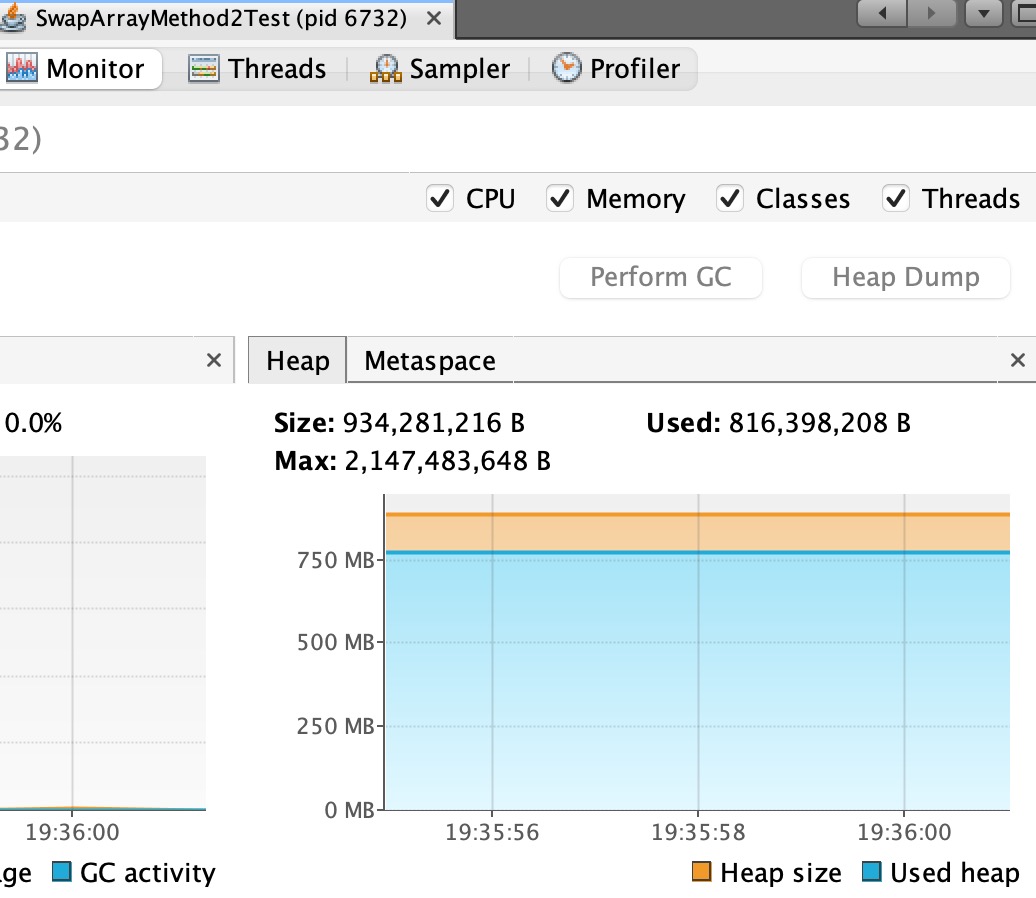
通过Used可以看到基本开辟数组的占用堆大小要比交换的多一倍。
这里我也修改了下在交换的形式下占用的空间尽管都是一个变量的修改,
但通过修改这个变量之后轮换的也是为O(n/2)
也就是说int temp这个数据即使是修改本身,也会将占用空间✖️它本身修改次数
现在我有点好奇Arrays.sort的效果会怎样,
因为Array.sort的逆序是只能针对装箱类型,装箱1E个数据基本不太可能等到结果,
那我的操作是使用一个已经逆序的数组int[],然后看他sort到正序是花费多久时间的。
可以从Arrays.sort底层代码看出其使用的是快排的思想:
java/util/DualPivotQuicksort.java:107
static void sort(int[] a, int left, int right,
int[] work, int workBase, int workLen) {
// Use Quicksort on small arrays
if (right - left < QUICKSORT_THRESHOLD) {
sort(a, left, right, true);
return;
}
这里可以看下快排的思想
但实际上JDK的大牛们远超我们的想象,
可以看到这个sort方法的注释,大牛的名字:
Dual-Pivot Quicksort by Vladimir Yaroslavskiy, Jon Bentley, and Joshua Bloch
而我这里最熟悉的就是Joshua Bloch(约书亚-布洛克),因为他是
《Effective Java》这本书的作者。是非常有名的Google大牛。
而其在sort的几个重载方法中,也有其绘制的算法的大概的描述:
/*
* Partitioning:
*
* left part center part right part
* +--------------------------------------------------------------+
* | < pivot1 | pivot1 <= && <= pivot2 | ? | > pivot2 |
* +--------------------------------------------------------------+
* ^ ^ ^
* | | |
* less k great
*
* Invariants:
*
* all in (left, less) < pivot1
* pivot1 <= all in [less, k) <= pivot2
* all in (great, right) > pivot2
*
* Pointer k is the first index of ?-part.
*/
而这个描述说明其快排使用了双轴(pivot)的方式,在原来one pivot的基础上,
进行了相应的扩展。而走哪个重载sort也是根据arr的大小和类型决定的。
其实这个逆序跟倒置是不同的,
Arrays.sort(arr,(a,b)->b-a)
与
Collections.reverse(arr)
效果不同
而reverse我看了也是根据交换的思想来的
public static void reverse(List<?> list) {
int size = list.size();
if (size < REVERSE_THRESHOLD || list instanceof RandomAccess) {
for (int i=0, mid=size>>1, j=size-1; i<mid; i++, j--)
swap(list, i, j);
} else {
// instead of using a raw type here, it's possible to capture
// the wildcard but it will require a call to a supplementary
// private method
ListIterator fwd = list.listIterator();
ListIterator rev = list.listIterator(size);
for (int i=0, mid=list.size()>>1; i<mid; i++) {
Object tmp = fwd.next();
fwd.set(rev.previous());
rev.set(tmp);
}
}
}
代码:
https://github.com/moocstudent/geektime-spring-family-learning/tree/master/algorithm-demo/src
参考:
https://zhuanlan.zhihu.com/p/374041792
只做大概研究,如有错误请看官指出谢谢!