GukiZ and Binary Operations CodeForces

 大意: 给定$n,k,l,m$, 求有多少个长度为$n$, 元素全部严格小于$2^l$, 且满足

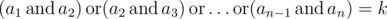的序列.

刚开始想着暴力枚举当前or和上一个数二进制中$1$的分布, 但这样状态数是$O(64^3)$在加上矩阵幂的复杂度显然不行.

看了题解发现可以按每位单独来考虑.

#include <iostream>
#include <sstream>
#include <algorithm>
#include <cstdio>
#include <math.h>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <string.h>
#include <bitset>
#define REP(i,a,n) for(int i=a;i<=n;++i)
#define PER(i,a,n) for(int i=n;i>=a;--i)
#define hr putchar(10)
#define pb push_back
#define lc (o<<1)
#define rc (lc|1)
#define mid ((l+r)>>1)
#define ls lc,l,mid
#define rs rc,mid+1,r
#define x first
#define y second
#define io std::ios::sync_with_stdio(false)
#define endl '
'
#define DB(a) ({REP(__i,1,n) cout<<a[__i]<<' ';hr;})
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int P = 1e9+7, P2 = 998244353, INF = 0x3f3f3f3f;
ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
ll qpow(ll a,ll n) {ll r=1%P;for (a%=P;n;a=a*a%P,n>>=1)if(n&1)r=r*a%P;return r;}
ll inv(ll x){return x<=1?1:inv(P%x)*(P-P/x)%P;}
inline int rd() {int x=0;char p=getchar();while(p<'0'||p>'9')p=getchar();while(p>='0'&&p<='9')x=x*10+p-'0',p=getchar();return x;}
//head




ll n, k, l, m;

struct Mat {
	int v[4][4];
	Mat() {memset(v, 0, sizeof v);}
	Mat operator * (const Mat& b) const {
		Mat c;
		REP(k,0,3) REP(i,0,3) REP(j,0,3) { 
			c.v[i][j] = ((ll)v[i][k]*b.v[k][j]+c.v[i][j])%m;
		}
		return c;
	}
	Mat operator ^ (ll nn) {
		Mat b, a=*this;
		REP(i,0,3) b.v[i][i]=1;
		while(nn) {
			if(nn&1LL) b=b*a;
			nn>>=1LL,a=a*a;
		}
		return b;
	}
};

int main() {
	cin>>n>>k>>l>>m;
	if (m==1||l<64&&(k>>l)) return puts("0"),0;
	Mat g;
	g.v[0][0]=g.v[0][2]=g.v[1][1]=g.v[1][3]=g.v[2][0]=g.v[3][1]=g.v[3][2]=g.v[3][3]=1;
	g = g^n;
	int x = (g.v[0][0]+g.v[2][0])%m, y = (g.v[1][0]+g.v[3][0])%m;
	ll ans = 1;
	REP(i,0,l-1) {
		if (k>>i&1) ans = ans*y%m;
		else ans = ans*x%m;
	}
	printf("%lld
", ans);
}