公约数的和
放在这么前面的位置当然是给自己看的!!!!!
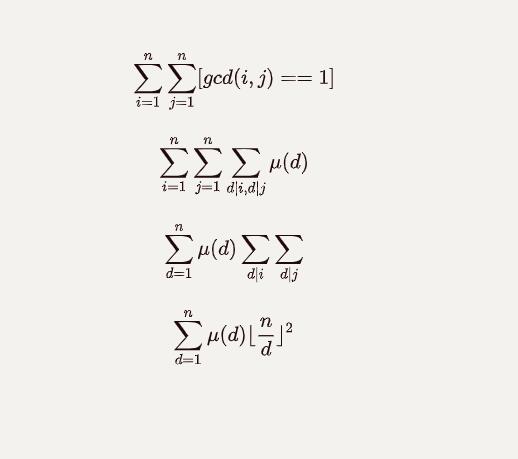
这一步原来是这么推过来的!如果下次再忘了怎么推可以这么搞出来或者直接记结论
分析
这道题很显然答案为
[Ans=sum_{i=1}^nsum_{j=i+1}^n (i,j)
]
//其中((i,j))意味(gcd(i,j))
这样做起来很烦,看起来是(O(N^2))的辣鸡复杂度,我们考虑这个问题的弱化版
求$$sum_{i=1}nsum_{j=1}n(i,j)$$
然后通过一些优美的容斥就可以算出原答案
现在我们设$$f(d)=sum_{i=1}nsum_{j=1}n[(i,j)=d]$$
这个式子表示,在(i=1..n,j=1..n,gcd(i,j)=d)的个数,其中([])内成立,返回值为(1),否则为(0)
我们令
[F(n)=sum_{n|d}f(d)=lfloorfrac N n
floor^2
]
则有
[f(n)=sum_{n|d}mu(frac d n)F(d)$$$$=sum_{n|d}mu(frac d n)lfloorfrac N d
floor^2
]
考虑(Ans)
[Ans=sum_{i=1}^nsum_{j=1}^n(i,j)
]
[=sum_{d=1}^n dsum_{i=1}^nsum_{j=1}^n[(i,j)=d]
]
[=sum_{d=1}^n d;f(d)
]
考虑把(f(d))的式子带入,这时我们不枚举(d)的倍数具体是多少,而是枚举倍数(不枚举(d|n)的(n),而是枚举(frac n d),比如说我们用(k)表示,就有
[=sum_{d=1}^N d sum_{k=1}^Nmu(k)lfloorfrac{N}{dk}
floor^2
]
这个(dk)感觉不是很舒服,我们令(t=dk,将枚举d改为枚举dk,则有)
[=sum_{t=1}^Nsum_{k|t} kmu(frac{t}{k})lfloorfrac{N}{t}
floor^2
]
观察$$sum_{k|t} kmu(frac{t}{k})$$
我们发现这是在前文提及的狄利克雷卷积
[mu imes d=phi
]
(忘了的话戳这里)
本篇·莫比乌斯反演
那么原式就优美的化简为
[sum_{t=1}^Nphi(t)lfloorfrac{N}{t}
floor^2
]
这样一个式子已经可以(O(N))地解决了,更优美地也可以进行整除分块,做到计算(sqrt{n})
关于最前面的容斥,只需要减去(gcd(i,i)=i)和(gcd(i,j)=gcd(j,i))的情况就可以
对于(gcd(i,i)=i)的情况,考虑在(sum_{i=1}^nsum_{j=1}^n(i,j))中,对于每个(i),有且仅有(1)个(j=i)对应,此时的贡献为(i),所以总贡献为
(sum_{i=1}^N i=N(N+1)/2)
而(gcd(i,j)=gcd(j,i))的情况,去掉情况(1)后显然这两个对半分,只要(/2)即可
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn=2000010;
LL sum[maxn];
int vis[maxn],phi[maxn],pri[maxn];
int cnt=0,n;
inline void getphi(int n){
memset(vis,0,sizeof(vis));phi[1]=vis[1]=1;
for (int i=2;i<=n;i++){
if (!vis[i]){pri[++cnt]=i;phi[i]=i-1;}
for (int j=1;j<=cnt&&(LL)i*pri[j]<=n;j++){
vis[i*pri[j]]=1;
if (i%pri[j]==0){phi[i*pri[j]]=phi[i]*pri[j];break;}
else phi[i*pri[j]]=phi[i]*(pri[j]-1);
}
}
for (int i=1;i<=n;i++) sum[i]=sum[i-1]+phi[i];
}
int main(){
scanf("%d",&n);
getphi(n);
LL ans=0;
for (int l=1,r;l<=n;l=r+1){
r=n/(n/l);
ans+=(LL)(sum[r]-sum[l-1])*(n/l)*(n/l);
}
printf("%lld",(ans-(LL)n*(n+1)/2)/2);
return 0;
}