完全二叉堆和堆排序

一，优先级队列

    数据集合中，各元素的访问顺序取决于元素自身的优先级(call-by-priority)。

二，拥有的操作接口

1.插入操作，inisert();

2.获取优先级最高的元素,getMax();

3.删除优先级最高的元素,deleteMax();

 三，构造优先级队列

    但是为什么使用堆来表示优先级队列呢，在实现优先级对列时，我们既要考虑效率，也要兼顾成本。所以最好的实现方式应该是这两个要求的综合体。

 1.使用普通线性数组(无序)来表示优先级队列。

• 执行插入操作时，直接将元素插入到数组末端，需要的成本为O(1),
• 获取优先级最高元素，我们需要遍历整个线性队列，匹配出优先级最高元素，需要的成本为Θ(n)
• 删除优先级最高元素，我们需要两个步骤，第一找出优先级最高元素，第二步删除优先级最高元素，然后将后面的元素依次迁移，填补空缺，需要的成本为Θ(n)+Θ(n)=Θ(n)

2.使用一个按顺序排列的有序向量实现优先级队列

• 获取优先级最高元素，O(1)
• 删除优先级最高元素，O(1)
• 插入一个元素，需要两个步骤，第一步我们需要找出要插的位置，这里我们可以使用二分查找，成本为O(logn)，第二步是插入元素之后，将

        其所有后继进行后移操作，成本为O(n)，所有总成本为O(logn)+O(n)=O(n)

3.使用BBST(AVL，伸展书，红黑树)实现优先级对列，从BBST的特性我们可以得出不管是插入，获取最高优先级元素，或者删除最高优先级元素其需要的成本都为O(log n)。这是个不错的效果。但是我们发现我们使用BBST来表示优先级队列时，在查找和删除操作时却只是用作最高优先级元素，这样就显得有些大材小用。

综上，我们发现，对于表示优先级对列，我们就需要去维护优先级最高的元素，而无需维护整个元素。

上面，我们使用基本的向量(数组)来表示时，效率不是很高，但是采用BBST时虽然效率很高，但是却有杀鸡用牛刀。所以我们考虑使用向量+树的结合体来表示优先级队列--完全二叉堆。

三，完全二叉树

在完全二叉树中，除了最后一层可能不满之外其他层都是满的，最后一层如果缺少的话。只缺少右边若干节点。

 

 

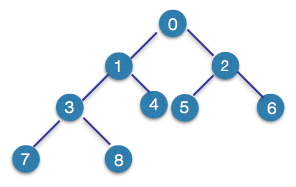
四，向量与二叉树结合

逻辑上：为二叉树

物理上：使用向量实现

                  图中的数值为它们的秩

我们看出，向量里的元素为完全二叉树按广度优先遍历的结果.

性质

1.对于节点i，如果其左孩子存在，则其左孩子为i*2+1

2.如果其右孩子存在，则其右孩子为（i+1）*2

3.如果其父节点存在，则其父节点为(i-1)/2

4.堆序性：堆有大顶堆和小顶堆，这里我们只考虑大顶堆，则对于大顶堆:

在数值上，如果i>0,则必有，H[i]≤H[Parent(i)],既任何一个节点在任何情况下的值都不会超过它的父亲

三，考虑大的元素(最高优先级)

根据上面的堆序性不难看出，最大的元素必然在堆顶,而堆顶的元素的秩为0，既getMax()操作只需返回内部数组中的首元素

这种优先级队列的表现方式在逻辑上借助了完全二叉树，人们有时也称它为完全二叉堆。 

三，二叉堆的实现

在实现优先级队列的插入，删除和获取最高优先级元素时，我们需要借助几个方法

1.下虑

void percolateDown(int heap[],int start,int end)
{

    int temp = heap[start];
 
    for (int j = 2 * start + 1 ; j < end ; j = 2 * j + 1) {
        
        while (j<end-1 && heap[j] <heap[j+1]) {
            j++;
        }
        
        if(temp >=heap[j])
            break;
        
        heap[start] = heap[j];
        start = j;
        
    }
    heap[start] = temp;
    
  
}

2.上虑

void percolateUp(int heap[],int start)
{
    int temp=0;
    int j = 0;
   
    
    while (start>0) {
    
         temp = heap[start];
         j = (start - 1)/2;
        
        if (heap[start]>heap[j]) {
            heap[start]=heap[j];
            heap[j]=temp;
            start=j;
    
        }else{
            break;
        }
        
    }

}

3.Floyed建堆算法

int createHeap(int heap[],int length)
{
    if (heap == NULL || length == 0) {
        return 0;
    }
  
    for (int i = length / 2 -1; i>=0; i--) {
        percolateDown(heap, i, length);
    }
    
    return 1;

}

int delete(int heap[],int *length)
{
    if (heap == NULL) {
        return 0;
    }
    
    heap[0] = heap[*length-1];
    (*length)--;
    percolateDown(heap, 0, *length);
    return 1;
    
}

4.在堆顶插入元素

int insert(int heap[],int value,int * length)
{
    if (heap == NULL) {
        return 0;
    }
    
    heap[*length] = value;
   
    percolateUp(heap, *length);
    (*length)++;
    return 1;


}