原理
选择子树最大的儿子, 将其归入当前点所在 的同一条重链,结束后树被分为一系列序号(dfs序)连续的重链,利用数据结构(线段树)来维护这些链的信息,最终可以实现树上的链操作(树链查询、树链修改)。
概念
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
轻儿子:父亲节点中除了重儿子以外的儿子;
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径;
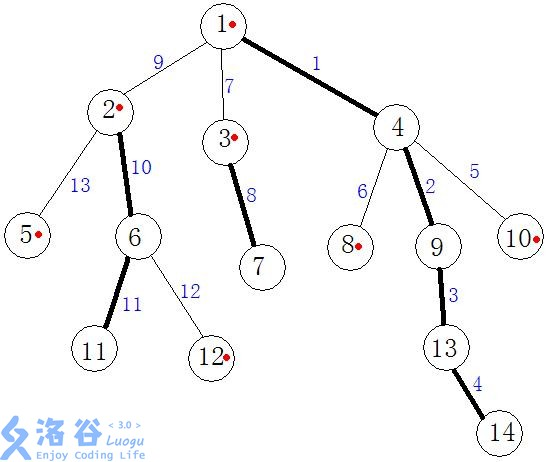
图中粗边就是剖分后的重边,细边是轻边
DFS序
按照从根节点进行DFS的顺序标记的节点标号。
入序:第一次搜索到时的序号
出序:回溯到父节点前的序号(入序加子树大小-1)
(上图中边上的数字就是靠下节点的DFS序)
特点:一个子树上的DFS序 一定是连续的,就是从子树根的入序~子树根的出序。
按照重链优先的方式标记的DFS序,保证了每条重链上的DFS序也一定是连续的。
模板
变量定义
struct edge{
int next,to;
}E[maxn+maxn];//双向边开两倍空间
ll n,q,tot=0,cnt=0,head[maxn];
ll d[maxn],fa[maxn],size[maxn],son[maxn];//深度,父节点,子树大小,重子节点
ll top[maxn],id1[maxn],rk[maxn],id2[maxn];//重链链头,dfs入序,dfs序对应的节点,出序
第一遍dfs,求出父节点、子树大小、节点深度、重子节点
void dfs1(int x){
size[x]=1;
d[x]=d[fa[x]]+1;
for(int i=head[x];i;i=E[i].next){//遍历与x相邻的边
if(E[i].to!=fa[x]){//遍历到不是父节点的点,都是儿子
fa[E[i].to]=x;
dfs1(E[i].to);
size[x]+=size[E[i].to];
if(size[E[i].to]>size[son[x]])//找到size最大的子树
son[x]=E[i].to;
}
}
}
第二遍dfs,求出各点的DFS序、在重链上的链头
void dfs2(int x,int tp){
id1[x]=++cnt;//入序
rk[cnt]=x;
top[x]=tp;
if(son[x]) dfs2(son[x],tp);//先搜索重儿子
for(int i=head[x];i;i=E[i].next ){
if(E[i].to!=fa[x] && E[i].to !=son[x])//i为轻边,新建链头
dfs2(E[i].to ,E[i].to );
}
id2[x]=cnt;//出序
}
LCA
//求x和y的最近公共祖先
int lca(int x,int y){
while(top[x]!=top[y]){
if(d[top[x]]<d[top[y]])
swap(x,y);//令x为较深节点
x=fa[top[x]];//x跳跃到链头的父节点
}
return d[x]<d[y]?x:y;//x,y在同一条重链上,公共祖先为深度浅的那个
}
//x为LCA,求LCA靠近y的第一个儿子
int lca2(int x,int y){
int t;
while(top[x]!=top[y])t=top[y],y=fa[top[y]];
return x==y?t:son[x];
}
链操作
void chain(int x,int y,int val){
for(;top[x]!=top[y];x=fa[top[x]]){
if(d[top[x]]<d[top[y]])swap(x,y);
op(id[top[x]],id[x],val);
//op(x,y,val) 表示对区间 [x,y] 进行值为 val 的操作,通常用 数据结构维护
}
if(d[x]<d[y])
swap(x,y);
op(id[y],id[x],val);
}
例题
大都市meg
https://cn.vjudge.net/contest/315785#problem/A
题意转化为:一棵树的节点权值初始化为节点深度。
操作一:将一个子树中所有节点权值减一
操作二:查询某个节点权值
解法:
利用dfs序在子树上连续的特点,按照dfs序建立单点查询,区间修改的线段树。
#include <iostream>
#include <cstdio>
using namespace std;
const int maxn=5e5+5;
struct edge{
int next;
int to;
int w;
}E[maxn+maxn];//存双向边要开两倍空间
int n,m,rt,tot=0,cnt=0;
int head[maxn];
int d[maxn],fa[maxn],size[maxn],son[maxn],top[maxn];
int id1[maxn],id2[maxn];//节点的dfs序
int rk[maxn];//dfs序对应的节点
const int M=1<<18;
int T[M+M+1];
void add(int l,int r,int w){
for(l+=M-1,r+=M+1;l^r^1;l>>=1,r>>=1){
if(~l&1) T[l^1]+=w;
if(r&1) T[r^1]+=w;
}
}
int query(int x){
int ans=0;
for(x+=M;x;x>>=1)
ans+=T[x];
return ans;
}
void dfs1(int x){
size[x]=1;
d[x]=d[fa[x]]+1;
for(int i=head[x];i;i=E[i].next){//遍历与x相邻的边
if(E[i].to!=fa[x]){//遍历到不是父节点的点,都是儿子
fa[E[i].to]=x;
dfs1(E[i].to);
size[x]+=size[E[i].to];
if(size[E[i].to]>size[son[x]])//找到size最大的子树
son[x]=E[i].to;
}
}
}
void dfs2(int x,int tp){
id1[x]=++cnt;
rk[cnt]=x;
top[x]=tp;
if(son[x]) dfs2(son[x],tp);//与重儿子链头相同
for(int i=head[x];i;i=E[i].next ){
if(E[i].to!=fa[x] && E[i].to !=son[x])//i为轻边,新建链头
dfs2(E[i].to ,E[i].to );
}
id2[x]=cnt;
}
void addedge(int u,int v,int w){
tot++;
E[tot].next=head[u];
head[u]=tot;
E[tot].to=v;
E[tot].w=w;
}
int main(){
cin>>n;
int x,y;
for(int i=1;i<=n-1;i++){
scanf("%d%d",&x,&y);
addedge(x,y,1);
addedge(y,x,1);
}
dfs1(1);
dfs2(1,1);
for(int i=1;i<=n;i++)
add(id1[i],id1[i],d[i]-1);
char c;
cin>>m;
for(int i=1;i<=n+m-1;i++){
scanf(" %c",&c);
if(c=='W'){
scanf("%d",&x);
printf("%d\n",query(id1[x]));
}
if(c=='A'){
scanf("%d%d",&x,&y);
if(d[x]<d[y]) swap(x,y);//x为子节点
add(id1[x],id2[x],-1);
}
}
}
树的统计Count
https://cn.vjudge.net/contest/315785#problem/B
树上单点修改,查询链上和/链上最值,模板题
重链剖分,重链上的DFS序连续,按照DFS序建立线段树,每次在重链上ans+=query()
#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
typedef long long ll;
const int maxn=3e4+5;
const ll INF=1e17;
struct edge{
int next,to;
}E[maxn+maxn];
ll n,q,tot=0,cnt=0,head[maxn];
ll d[maxn],fa[maxn],size[maxn],son[maxn];
ll top[maxn],id[maxn],rk[maxn],id2[maxn];
void addedge(ll u,ll v){
tot++;
E[tot].next=head[u];
E[tot].to=v;
head[u]=tot;
}
void dfs1(ll u){
size[u]=1;
d[u]=d[fa[u]]+1;
for(ll i=head[u];i;i=E[i].next){
if(E[i].to!=fa[u]){
fa[E[i].to]=u;
dfs1(E[i].to);
size[u]+=size[E[i].to];
if(size[E[i].to]>size[son[u]])
son[u]=E[i].to;
}
}
}
void dfs2(ll u,ll tp){
top[u]=tp;
id[u]=++cnt;
rk[cnt]=u;
if(son[u])dfs2(son[u],tp);
for(ll i=head[u];i;i=E[i].next){
if(E[i].to!=fa[u]&&E[i].to!=son[u])
dfs2(E[i].to,E[i].to);
}
id2[u]=cnt;
}
const ll M=1<<15;
ll T1[M+M+1],T2[M+M+1];//1:区间和,2:区间最值
void modify1(ll n,ll w){
for(T1[n+=M]=w,n>>=1;n;n>>=1)
T1[n]=T1[n+n]+T1[n+n+1];
}
ll query1(ll l,ll r){
ll ans=0;
for(l+=M-1,r+=M+1;l^r^1;l>>=1,r>>=1){
if(~l&1) ans+=T1[l^1];
if(r&1) ans+=T1[r^1];
}
return ans;
}
void modify2(ll n,ll w){
for(T2[n+=M]=w,n>>=1;n;n>>=1)
T2[n]=max(T2[n+n],T2[n+n+1]);
}
ll query2(ll l,ll r){
ll lmax=-INF,rmax=-INF;
for(l+=M-1,r+=M+1;l^r^1;l>>=1,r>>=1){
if(~l&1) lmax=max(lmax,T2[l^1]);
if(r&1) rmax=max(rmax,T2[r^1]);
}
return max(lmax,rmax);
}
ll qt1(ll u, ll v){
ll ans=0;
while(top[u]!=top[v]){
if(d[top[u]]<d[top[v]])
swap(u,v);
ans+=query1(id[top[u]],id[u]);
u=fa[top[u]];
}
if(d[u]<d[v]) swap(u,v);
ans+=query1(id[v],id[u]);
return ans;
}
ll qt2(ll u, ll v){
ll ans=-INF;
while(top[u]!=top[v]){
if(d[top[u]]<d[top[v]])
swap(u,v);
ans=max(ans,query2(id[top[u]],id[u]) );
u=fa[top[u]];
}
if(d[u]<d[v]) swap(u,v);
ans=max(ans,query2(id[v],id[u]) );
return ans;
}
int main(){
ll n;
cin>>n;
ll x,y;
for(int i=1;i<=n-1;i++){
scanf("%lld%lld",&x,&y);
addedge(x,y);
addedge(y,x);
}
dfs1(1);//1作为根节点
dfs2(1,1);
for(int i=1;i<=n;i++){
scanf("%lld",&x);
modify1(id[i],x);
modify2(id[i],x);
}
char s[10];
ll m;
cin>>m;
for(int i=1;i<=m;i++){
scanf("%s%lld%lld",s,&x,&y);
if(s[1]=='H'){
modify1(id[x],y);
modify2(id[x],y);
}
if(s[1]=='S')
printf("%lld\n",qt1(x,y));
if(s[1]=='M')
printf("%lld\n",qt2(x,y));
}
}
遥远的国度
https://cn.vjudge.net/contest/315785#problem/C
树上的子树查询;树的换根;线段树区间覆盖,最小值查询。
换根时记录新根即可不重新建树,每次询问时判断新根是否在原子树中。
1、新根不在原子树中,直接用线段树query即可
2、新根和询问节点相同,直接询问整个线段树的最小值
3、新根在原子树中,需要先求出询问节点到新根路径上的第一个点tv,在线段树上求tv的子树的补集的最小值即可。补集范围需要分类讨论,tv的入序为id1[tv],出序为id2[tv],若id1[tv]-1和id2[tv]+1均未超出线段树边界,则补集为(1,id1[tv]-1)\(\cup\)(id2[tv]+1,n),有一个超出范围就不考虑那一个。
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const ll INF=1e18;
ll n,m;
//树链剖分---------------------------------------------------
struct edge{
ll next;
ll to;
}E[maxn+maxn];//存双向边要开两倍空间
ll rt,tot=0,cnt=0;
ll head[maxn];
ll d[maxn],fa[maxn],size[maxn],son[maxn],top[maxn];
ll id1[maxn],id2[maxn];//节点的dfs序
ll rk[maxn];//dfs序对应的节点
void dfs1(ll x){
size[x]=1;
d[x]=d[fa[x]]+1;
for(ll i=head[x];i;i=E[i].next){//遍历与x相邻的边
if(E[i].to!=fa[x]){//遍历到不是父节点的点,都是儿子
fa[E[i].to]=x;
dfs1(E[i].to);
size[x]+=size[E[i].to];
if(size[E[i].to]>size[son[x]])//找到size最大的子树
son[x]=E[i].to;
}
}
}
void dfs2(ll x,ll tp){
id1[x]=++cnt;
rk[cnt]=x;
top[x]=tp;
if(son[x]) dfs2(son[x],tp);//与重儿子链头相同
for(ll i=head[x];i;i=E[i].next ){
if(E[i].to!=fa[x] && E[i].to !=son[x])//i为轻边,新建链头
dfs2(E[i].to ,E[i].to );
}
id2[x]=cnt;
}
//求x和y的最近公共祖先
int lca(int x,int y){
while(top[x]!=top[y]){
if(d[top[x]]<d[top[y]])
swap(x,y);//令x为较深节点
x=fa[top[x]];//x跳跃到链头的父节点
}
return d[x]<d[y]?x:y;//x,y在同一条重链上,公共祖先为深度浅的那个
}
//x为LCA,求LCA靠近y的第一个儿子
int lca2(int x,int y){
int t;
while(top[x]!=top[y])t=top[y],y=fa[top[y]];
return x==y?t:son[x];
}
void addedge(ll u,ll v){
tot++;
E[tot].next=head[u];
head[u]=tot;
E[tot].to=v;
}
//线段树-------------------------------------------------
ll w[maxn],wt[maxn],root;
struct node{
ll l,r,ans,lazy;
node():l(0),r(0),ans(0),lazy(0){}
}T[4*maxn];
inline void update(ll k){
T[k].ans=min(T[k<<1].ans,T[k<<1|1].ans);
}
inline void push_down(ll x){
if(T[x].lazy==0)return;
T[x<<1].lazy=T[x].lazy;
T[x<<1|1].lazy=T[x].lazy;
T[x<<1].ans=T[x].lazy;
T[x<<1|1].ans=T[x].lazy;
T[x].lazy=0;
}
void build(ll rt,ll l,ll r){
T[rt].l=l;T[rt].r=r;
if(l==r){
T[rt].ans=wt[l];return;
}
ll mid=(l+r)>>1;
build(rt<<1,l,mid);
build(rt<<1|1,mid+1,r);
update(rt);
}
ll query(ll rt,ll l,ll r){
if(l<=T[rt].l && T[rt].r<=r)
return T[rt].ans;
if(T[rt].r<l || T[rt].l>r) return 0;
push_down(rt);
ll ans=INF;
if(T[rt<<1].r>=l) ans=min(ans,query(rt<<1,l,r));
if(T[rt<<1|1].l<=r) ans=min(ans,query(rt<<1|1,l,r));
return ans;
}
void modify(ll rt,ll l,ll r,ll w){
if(l<=T[rt].l&&T[rt].r<=r){
T[rt].ans=w;
T[rt].lazy=w;
return;
}
push_down(rt);
if(T[rt<<1].r>=l) modify(rt<<1,l,r,w);
if(T[rt<<1|1].l<=r) modify(rt<<1|1,l,r,w);
update(rt);
}
void treem(ll u,ll v,ll val){
for(;top[u]!=top[v];u=fa[top[u]]){
if(d[top[u]]<d[top[v]])
swap(u,v);
modify(1,id1[top[u]],id1[u],val);
}
if(d[u]<d[v])
swap(u,v);
modify(1,id1[v],id1[u],val);
}
void treeq(ll u){
if(u==root){//根为子树
printf("%lld\n",query(1,1,n) );
}
else if(id1[u]<=id1[root]&&id1[root]<=id2[u]){//新根在子树中
ll tv=lca2(u,root);
ll ans=INF;
if(id1[tv]-1>=1) ans=min(ans,query(1,1,id1[tv]-1));
if(id2[tv]+1<=n) ans=min(ans,query(1,id2[tv]+1,n) );
printf("%lld\n",ans);
}
else{//新根在子树外
printf("%lld\n",query(1,id1[u],id1[u]+size[u]-1) );
}
}
int main(){
cin>>n>>m;
ll ef,et;
for(int i=1;i<=n-1;i++){
scanf("%lld%lld",&ef,&et);
addedge(ef,et);
addedge(et,ef);
}
for(int i=1;i<=n;i++) scanf("%lld",&w[i]);
dfs1(1);
dfs2(1,1);
for(int i=1;i<=n;i++) wt[i]=w[rk[i]];
build(1,1,n);
scanf("%lld",&root);
ll opt,p1,p2,v,id;
for(int i=1;i<=m;i++){
scanf("%lld",&opt);
if(opt==1){
scanf("%lld",&id);
root=id;
}
if(opt==2){
scanf("%lld%lld%lld",&p1,&p2,&v);
treem(p1,p2,v);
}
if(opt==3){
scanf("%lld",&id);
treeq(id);
}
}
}