1.矩阵了解
1)矩阵的维度和记法
(先数多少行,再数多少列)

2)矩阵的转置
行变成列,第一行变成第一列...矩阵的转置的转置就是原矩阵
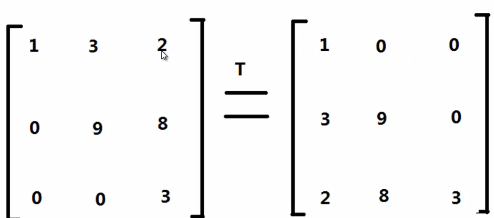 即
即 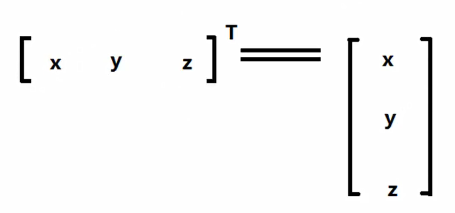
3)矩阵和标量的乘法
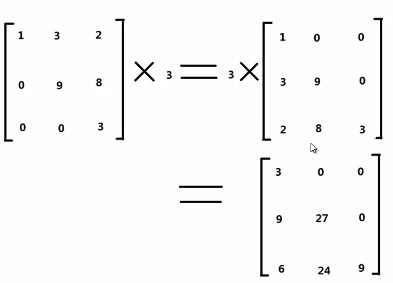
4)矩阵和矩阵的乘法
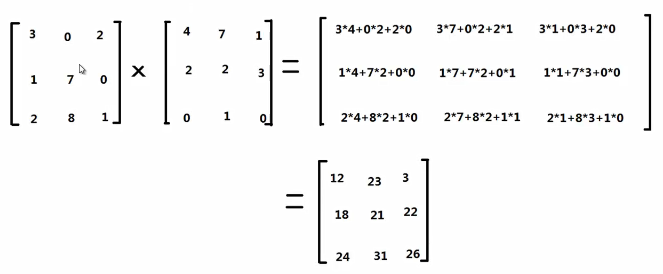
例.[2,3]X[3,4] =[2,4]
矩阵的乘法不支持交换律,强调顺序,左乘和右乘是不一样的。
NXM阶与SXT阶矩阵相乘,必须满足M和S维度相同,乘法的结果是一个NXT矩阵。
5)单位矩阵
主对角线全部为1,非主对角线都为0,则为单位矩阵。
单位矩阵乘任何矩阵,任何矩阵都不变。

2.矩阵变换
1)2D变换
①绕坐标中心旋转a角度
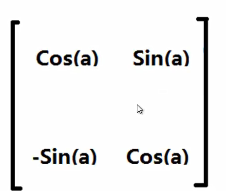
②缩放矩阵
沿坐标轴缩放
(k分别为x轴,y轴上缩放因子)
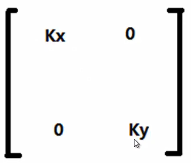
沿任意N轴缩放
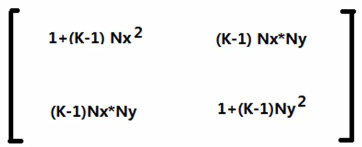
2)3D变换
①绕x,y,z轴旋转a度
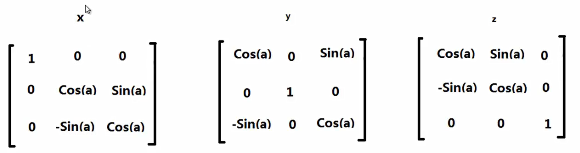
②缩放矩阵
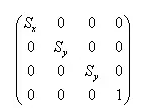
3)变换的种类
旋转 缩放 平移 镜像
切边(正方形上面拉一下,变成平行四边形,称之为切边)
投影(分为 平行投影:Unity中正交相机,对物体大小不产生变化;透视投影:近大远小效果)
可逆(施加了一个变换,还可以撤销)
总结分类:
线性变换
仿射变换:线性变换+平移。
所有的线性变换都是仿射变换,但并不是所有的仿射变换是线性变换。
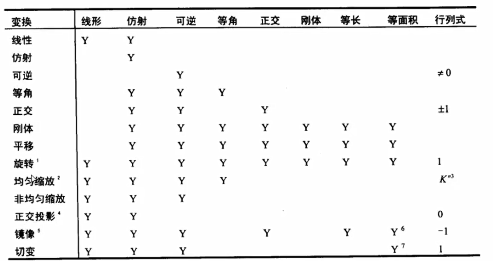
4)常见变换组合
满足结合律 a*b*c = a*(b*c)


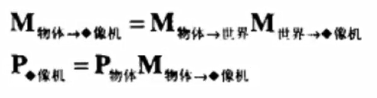
总结:一般可以使用矩阵转换工具进行变换。物体只需要乘一次工具矩阵即可完成变换。
3.变换深入
当我们使用2x2旋转过后,我们只需要旋转后的xy分量各自加上也可。但是没有一个统一的工具去解决。为了能够
把平移和其他的线性变换都组合在一起,利用矩阵这一工具去实现。我们需要把这个矩阵做一个扩展,在2d中平移需要扩展
为3x3的矩阵。
1)2D平移(3X3矩阵)
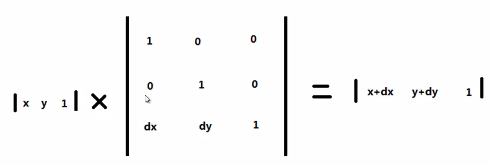
最后一个分量为何不取0?
第一次做了平移之后如果为0,又要做平移,参与第二次分量计算,因为其分量为0,都为0了。所以没有达到平移的目的。
2)3D平移(4X4矩阵)

3)3D 旋转+平移

4)透视投影(近大远小)
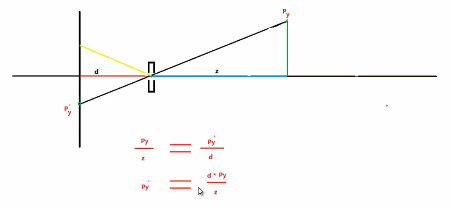
注意:这边本可以比较简单的使用等角三角形原理进行计算,但是还是使用矩阵来进行计算,因为可以方便的和其他
矩阵进行组合计算。
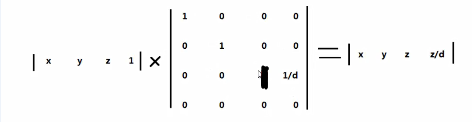
注意:这边的最后一个坐标分量的值不是1.
4.方阵
定义:行数和列数相等。
1)二阶方阵行列式

2)三阶方阵行列式
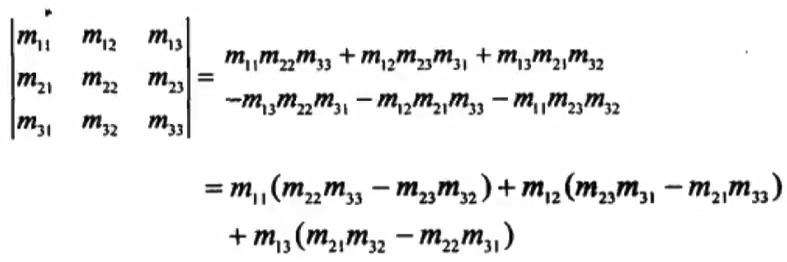
3)4阶行列式计算
代数余子式
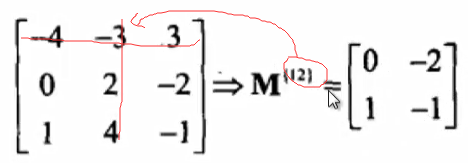
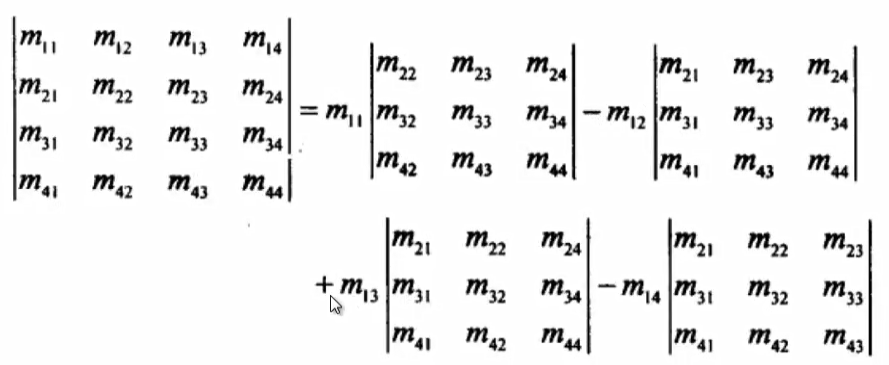
从方阵中任选一行中数,用这一行中每个元素去乘每个代数余子式。
注意计算方式,正负值取决于行列下标(1开始的)
行列式性质:
矩阵积的行列式等于矩阵行列式的积:|AB| =|A||B|
矩阵转置的行列式等于原矩阵的行列式:|M的转置| =|M|
如果矩阵的任意行或列全为0,那么他的行列式等于0
“把矩阵的任意两行或两列进行交换”,行列式变负
任意行或列的非零积加到另一行或列上不会改变行列式的值
4)矩阵的逆
①逆的定义
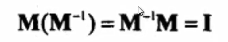
对于一个矩阵是否有逆,如果一个方阵他的行列式为0,成为奇异矩阵,没有逆。
有逆,则他的行列式一定不为0.
代数余子式矩阵(对矩阵中每一个元素都取代数余子式)
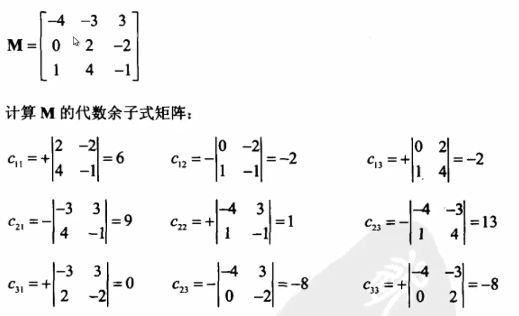
标准伴随矩阵
当我们得到代数余子式矩阵之后,需要把这个代数余子式矩阵进行转置,称为标准伴随矩阵。
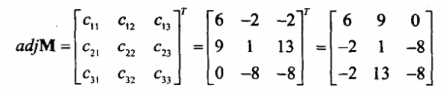
矩阵求逆 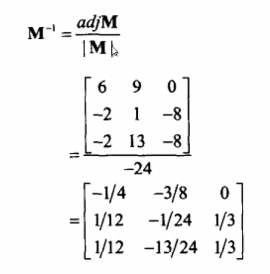
定义检测
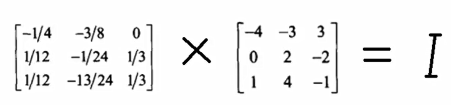
(主对角线都为1,其他都为0)
②矩阵逆 性质

③正交矩阵和逆
若方阵M是正交的,则当且仅当M与它的转置的乘积等于单位矩阵。
M*M的转置 = I(单位矩阵),即如果发现他是正交的,则可以把他的转置当做逆来使用。
应用:
仅仅拥有旋转,仅仅包含镜像。都是正交的。如果要撤销一个旋转,不用去求他的逆,直接用他的
转置就可以代替逆来使用。