Delta-wave
Time Limit : 2000/1000ms (Java/Other) Memory Limit : 65536/32768K (Java/Other)
Total Submission(s) : 35 Accepted Submission(s) : 9
Font: Times New Roman | Verdana | Georgia
Font Size: ← →
Problem Description
A triangle field is numbered with successive integers in the way shown on the picture below.
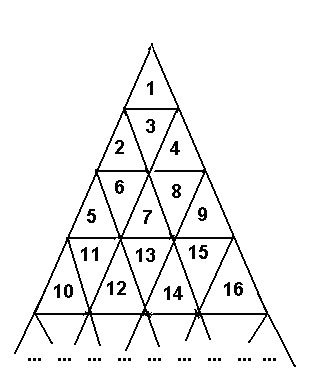
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.
Write the program to determine the length of the shortest route connecting cells with numbers N and M.

The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.
Write the program to determine the length of the shortest route connecting cells with numbers N and M.
Input
Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).
Output
Output should contain the length of the shortest route.
Sample Input
6 12
Sample Output
3
#include<stdio.h>
#include<math.h>
void find(int n,int &l,int &r,int &level)
{
int i;
level=1;
for(i=1;;i+=2)
{
if(n-i<=0)
{
l=(n+1)/2;
r=(i-n)/2+1;
break;
}
level++;
n-=i;
}
}
int main()
{
int m,n;
int ml,mr,nl,nr,mlevel,nlevel;
while(scanf("%d%d",&m,&n)!=EOF)
{
find(m,ml,mr,mlevel);
find(n,nl,nr,nlevel);
printf("%d
",abs(ml-nl)+abs(mr-nr)+abs(mlevel-nlevel));
}
return 0;
}
/* hdu Delta-wave 每个数,求出相对顶层的层数 up,相对于三角形左边界的层数 left, 相对于三角形右边界的层数 right
任意两个数的最短路径等于 顶层差 + 左边界差 + 右边界差 */
#include<stdio.h> #include<math.h> int abs(int a) { return (a>0)?a:-a; } int main() { int m,n; int ml,mr,nl,nr; int up1,up2,left1,left2,right1,right2; while(scanf("%d%d",&m,&n)!=EOF) { up1 = (int)ceil(sqrt((double)m)); //数m对应从上开始的层数 ml = (up1-1)*(up1-1)+1; //up1层最左边数的编号 mr = up1*up1; //up1层最右边数的编号 left1 = (m-ml)/2+1; //从m 到 左边界的层数 right1 = (mr-m)/2+1; //从m 到 到右边界的层数 up2 = (int)ceil(sqrt((double)n)); //数n对应从上开始的层数 nl = (up2-1)*(up2-1)+1; //up2层最左边数的编号 nr = up2*up2; //up2层最右边数的编号 left2 = (n-nl)/2+1; //从n 到 左边界的层数 right2 = (nr-n)/2+1; //从n 到 到右边界的层数 printf("%d ",abs(up2-up1)+abs(left2-left1)+abs(right2-right1)); } return 0; }*/
